
Partition topology
Encyclopedia
In mathematics
, the partition topology is a topology
that can be induced on any set X by partitioning
X into disjoint subsets P; these subsets form the basis for the topology. There are two important examples which have their own names:
The trivial partitions yield the discrete topology (each point of X is a set in P) or indiscrete topology (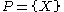 ).
).
Any set X with a partition topology generated by a partition P can be viewed as a pseudometric space
with a pseudometric given by:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the partition topology is a topology
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
that can be induced on any set X by partitioning
Partition of a set
In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
X into disjoint subsets P; these subsets form the basis for the topology. There are two important examples which have their own names:
- The odd–even topology is the topology where
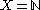 and
and 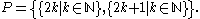
- The deleted integer topology is defined by letting
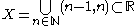 and
and 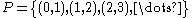 .
.
The trivial partitions yield the discrete topology (each point of X is a set in P) or indiscrete topology (
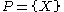 ).
).Any set X with a partition topology generated by a partition P can be viewed as a pseudometric space
Pseudometric space
In mathematics, a pseudometric space is a generalized metric space in which the distance between two distinct points can be zero. In the same way as every normed space is a metric space, every seminormed space is a pseudometric space...
with a pseudometric given by:
-
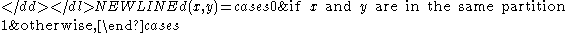
This is not a metric unless P yields the discrete topology.
The partition topology provides an important example of the independence of various separation axioms. Unless P is trivial, at least one set in P contains more than one point, and the elements of this set are topologically indistinguishable: the topology does not separate points. Hence X is not a Kolmogorov spaceKolmogorov spaceIn topology and related branches of mathematics, a topological space X is a T0 space or Kolmogorov space if for every pair of distinct points of X, at least one of them has an open neighborhood not containing the other. This condition, called the T0 condition, is one of the separation axioms...
, nor a T1 spaceT1 spaceIn topology and related branches of mathematics, a T1 space is a topological space in which, for every pair of distinct points, each has an open neighborhood not containing the other. An R0 space is one in which this holds for every pair of topologically distinguishable points...
, a Hausdorff spaceHausdorff spaceIn topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
or an Urysohn space. In a partition topology the complement of every open set is also open, and therefore a set is open if and only if it is closed. Therefore, X is a regularRegular spaceIn topology and related fields of mathematics, a topological space X is called a regular space if every non-empty closed subset C of X and a point p not contained in C admit non-overlapping open neighborhoods. Thus p and C...
, completely regular, normalNormal spaceIn topology and related branches of mathematics, a normal space is a topological space X that satisfies Axiom T4: every two disjoint closed sets of X have disjoint open neighborhoods. A normal Hausdorff space is also called a T4 space...
and completely normal.
We note also that X/P is the discrete topology.

