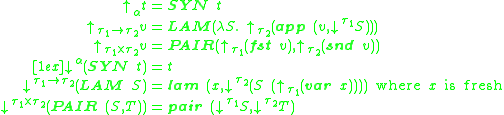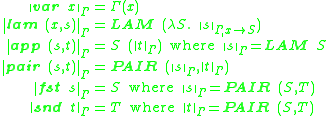Normalisation by evaluation
Encyclopedia
In programming language
semantics
, normalisation by evaluation (NBE) is a style of obtaining the normal form
of terms in the λ calculus by appealing to their denotational semantics
. A term is first interpreted into a denotational model of the λ-term structure, and then a canonical (β-normal and η-long) representative is extracted by reifying the denotation. Such an essentially semantic approach differs from the more traditional syntactic description of normalisation as a reductions in a term rewrite system where β-reductions are allowed deep inside λ-terms.
NBE was first described for the simply typed lambda calculus
. It has since been extended both to weaker type system
s such as the untyped lambda calculus using a domain theoretic
approach, and to richer type systems such as several variants of Martin-Löf type theory.
, where types τ can be basic types (α), function types (→), or products (×), given by the following Backus–Naur Form
grammar (→ associating to the right, as usual):
τ ::= α | τ1 → τ2 | τ1 × τ2
These can be implemented as a datatype in the meta-language; for example, for Standard ML
, we might use:
Terms are defined at two levels. The lower syntactic level (sometimes called the dynamic level) is the representation that one intends to normalise.
s,t,… ::= var x | lam (x, t) | app (s, t) | pair (s, t) | fst t | snd t
Here lam/app (resp. pair/fst,snd) are the intro/elim forms for → (resp. ×), and x are variables
. These terms are intended to be implemented as a first-order
in the meta-language:
The denotational semantics
of (closed) terms in the meta-language interprets the constructs of the syntax in terms of features of the meta-language; thus, lam is interpreted as abstraction, app as application, etc. The semantic objects constructed are as follows:
S,T,… ::= LAM (λx. S x) | PAIR (S, T) | SYN t
Note that there are no variables or elimination forms in the semantics; they are represented simply as syntax. These semantic objects are represented by the following datatype:
There are a pair of type-indexed functions that move back and forth between the syntactic and semantic layer
. The first function, usually written ↑τ, reflects the term syntax into the semantics, while the second reifies the semantics as a syntactic term (written as ↓τ). Their definitions are mutually recursive as follows:
These definitions are easily implemented in the meta-language:
By induction
on the structure of types, it follows that if the semantic object S denotes a well-typed term s of type τ, then reifying the object (i.e., ↓τ S) produces the β-normal η-long form of s. All that remains is, therefore, to construct the initial semantic interpretation S from a syntactic term s. This operation, written ∥s∥Γ, where Γ is a context of bindings, proceeds by induction solely on the term structure:
In the implementation:
Note that there are many non-exhaustive cases; however, if applied to a closed well-typed term, none of these missing cases are ever encountered. The NBE operation on closed terms is then:
As an example of its use, consider the syntactic term
This is the well-known encoding of the identity function
in combinatory logic
. Normalising it at an identity type produces:
The result is actually in η-long form, as can be easily seen by normalizing it at a different identity type:
Programming language
A programming language is an artificial language designed to communicate instructions to a machine, particularly a computer. Programming languages can be used to create programs that control the behavior of a machine and/or to express algorithms precisely....
semantics
Formal semantics of programming languages
In programming language theory, semantics is the field concerned with the rigorous mathematical study of the meaning of programming languages and models of computation...
, normalisation by evaluation (NBE) is a style of obtaining the normal form
Normal form
Normal form may refer to:* Normal form * Normal form * Normal form * Normal form In formal language theory:* Beta normal form* Chomsky normal form* Greibach normal form* Kuroda normal form...
of terms in the λ calculus by appealing to their denotational semantics
Denotational semantics
In computer science, denotational semantics is an approach to formalizing the meanings of programming languages by constructing mathematical objects which describe the meanings of expressions from the languages...
. A term is first interpreted into a denotational model of the λ-term structure, and then a canonical (β-normal and η-long) representative is extracted by reifying the denotation. Such an essentially semantic approach differs from the more traditional syntactic description of normalisation as a reductions in a term rewrite system where β-reductions are allowed deep inside λ-terms.
NBE was first described for the simply typed lambda calculus
Simply typed lambda calculus
The simply typed lambda calculus , a formof type theory, is a typed interpretation of the lambda calculus with only one type constructor: \to that builds function types. It is the canonical and simplest example of a typed lambda calculus...
. It has since been extended both to weaker type system
Type system
A type system associates a type with each computed value. By examining the flow of these values, a type system attempts to ensure or prove that no type errors can occur...
s such as the untyped lambda calculus using a domain theoretic
Domain theory
Domain theory is a branch of mathematics that studies special kinds of partially ordered sets commonly called domains. Consequently, domain theory can be considered as a branch of order theory. The field has major applications in computer science, where it is used to specify denotational...
approach, and to richer type systems such as several variants of Martin-Löf type theory.
Outline
Consider the simply typed lambda calculusSimply typed lambda calculus
The simply typed lambda calculus , a formof type theory, is a typed interpretation of the lambda calculus with only one type constructor: \to that builds function types. It is the canonical and simplest example of a typed lambda calculus...
, where types τ can be basic types (α), function types (→), or products (×), given by the following Backus–Naur Form
Backus–Naur form
In computer science, BNF is a notation technique for context-free grammars, often used to describe the syntax of languages used in computing, such as computer programming languages, document formats, instruction sets and communication protocols.It is applied wherever exact descriptions of...
grammar (→ associating to the right, as usual):
τ ::= α | τ1 → τ2 | τ1 × τ2
These can be implemented as a datatype in the meta-language; for example, for Standard ML
Standard ML
Standard ML is a general-purpose, modular, functional programming language with compile-time type checking and type inference. It is popular among compiler writers and programming language researchers, as well as in the development of theorem provers.SML is a modern descendant of the ML...
, we might use:
datatype ty = Basic of string
| Arrow of ty * ty
| Prod of ty * ty
Terms are defined at two levels. The lower syntactic level (sometimes called the dynamic level) is the representation that one intends to normalise.
s,t,… ::= var x | lam (x, t) | app (s, t) | pair (s, t) | fst t | snd t
Here lam/app (resp. pair/fst,snd) are the intro/elim forms for → (resp. ×), and x are variables
Variable (programming)
In computer programming, a variable is a symbolic name given to some known or unknown quantity or information, for the purpose of allowing the name to be used independently of the information it represents...
. These terms are intended to be implemented as a first-order
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
in the meta-language:
datatype tm = var of string
| lam of string * tm | app of tm * tm
| pair of tm * tm | fst of tm | snd of tm
The denotational semantics
Denotational semantics
In computer science, denotational semantics is an approach to formalizing the meanings of programming languages by constructing mathematical objects which describe the meanings of expressions from the languages...
of (closed) terms in the meta-language interprets the constructs of the syntax in terms of features of the meta-language; thus, lam is interpreted as abstraction, app as application, etc. The semantic objects constructed are as follows:
S,T,… ::= LAM (λx. S x) | PAIR (S, T) | SYN t
Note that there are no variables or elimination forms in the semantics; they are represented simply as syntax. These semantic objects are represented by the following datatype:
datatype sem = LAM of (sem -> sem)
| PAIR of sem * sem
| SYN of tm
There are a pair of type-indexed functions that move back and forth between the syntactic and semantic layer
Semantic layer
A semantic layer is a business representation of corporate data that helps end users access data autonomously using common business terms. Developed and patented by Business Objects, it maps complex data into familiar business terms such as product, customer, or revenue to offer a unified,...
. The first function, usually written ↑τ, reflects the term syntax into the semantics, while the second reifies the semantics as a syntactic term (written as ↓τ). Their definitions are mutually recursive as follows:
These definitions are easily implemented in the meta-language:
(* reflect : ty -> tm -> sem *)
fun reflect (Arrow (a, b)) t =
LAM (fn S => reflect b (app t (reify a S)))
| reflect (Prod (a, b)) t =
PAIR (reflect a (fst t)) (reflect b (snd t))
| reflect (Basic _) t =
SYN t
(* reify : ty -> sem -> tm *)
and reify (Arrow (a, b)) (LAM S) =
let x = fresh_var in
Lam (x, reify b (S (reflect a (var x))))
end
| reify (Prod (a, b)) (PAIR S T) =
Pair (reify a S, reify b T)
| reify (Basic _) (SYN t) = t
By induction
Mathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
on the structure of types, it follows that if the semantic object S denotes a well-typed term s of type τ, then reifying the object (i.e., ↓τ S) produces the β-normal η-long form of s. All that remains is, therefore, to construct the initial semantic interpretation S from a syntactic term s. This operation, written ∥s∥Γ, where Γ is a context of bindings, proceeds by induction solely on the term structure:
In the implementation:
(* meaning : ctx -> tm -> sem *)
fun meaning G t =
case t of
var x => lookup G x
| lam (x, s) => LAM (fn S => meaning (add G (x, S)) s)
| app (s, t) => (case meaning G s of
LAM S => S (meaning G t))
| pair (s, t) => PAIR (meaning G s, meaning G t)
| fst s => (case meaning G s of
PAIR (S, T) => S)
| snd t => (case meaning G t of
PAIR (S, T) => T)
Note that there are many non-exhaustive cases; however, if applied to a closed well-typed term, none of these missing cases are ever encountered. The NBE operation on closed terms is then:
(* nbe : ty -> tm -> tm *)
fun nbe a t = reify a (meaning empty t)
As an example of its use, consider the syntactic term
SKK defined below:
val K = lam ("x", lam ("y", var "x"))
val S = lam ("x", lam ("y", lam ("z", app (app (var "x", var "z"), app (var "y", var "z")))))
val SKK = app (app (S, K), K)
This is the well-known encoding of the identity function
Identity function
In mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
in combinatory logic
Combinatory logic
Combinatory logic is a notation introduced by Moses Schönfinkel and Haskell Curry to eliminate the need for variables in mathematical logic. It has more recently been used in computer science as a theoretical model of computation and also as a basis for the design of functional programming...
. Normalising it at an identity type produces:
- nbe (Arrow (Basic "a", Basic "a")) SKK;
val it = lam ("v0",var "v0") : tm
The result is actually in η-long form, as can be easily seen by normalizing it at a different identity type:
- nbe (Arrow (Arrow (Basic "a", Basic "b"), Arrow (Basic "a", Basic "b"))) SKK;
val it = lam ("v1",lam ("v2",app (var "v1",var "v2"))) : tm