Necklace splitting problem
Encyclopedia
In mathematics
, and in particular combinatorics
, the necklace splitting problem arises in a variety of contexts including exact division
; its picturesque name is due to mathematicians Noga Alon
and Douglas B. West.
Suppose a necklace
, open at the clasp, has k ·n beads. There are k · ai beads of colour i, where 1 ≤ i ≤ t. Then the necklace splitting problem is to find a partition of the necklace into k parts (not necessarily contiguous), each of which has exactly ai beads of colour i; such a split is called a k-split. The size of the split is the number of cuts that are needed to separate the parts (the opening at the clasp is not included). Inevitably, one interesting question is to find a split of minimal size.
Alon explains that
If the beads of each colour are contiguous on the open necklace, then any k splitting must contain at least k − 1 cuts, so the size is at least (k − 1)t. Alon and West use the Borsuk-Ulam theorem to prove that a k-splitting can always be achieved with this number of cuts. Alon uses these and related ideas to state and prove a generalization of the Hobby–Rice theorem
.
If the necklace is arranged so that no t-split is possible, then for any two subsets D1 and D2 of { 1, 2, ..., t }, not both empty, such that
, a (t − 1)-split exists such that:
I.e. if the thieves have preferences in the form of two "preference" sets D1 and D2, not both empty, there exists a (t − 1)-split so that thief 1 gets more beads of types in his preference set D1 than thief 2; thief 2 gets more beads of types in her preference set D2 than thief 1; and the rest are equal.
Simonyi credits Gábor Tardos with noticing that the result above is a direct generalization of Alon's original necklace theorem in the case k = 2. Either the necklace has a (t − 1)-split, or it does not. If it does, there is nothing to prove. If it does not, we may add beads of a fictitious colour to the necklace, and make D1 consist of the fictitious colour and D2 empty. Then Simonyi's result shows that there is a t-split with equal numbers of each real colour.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, and in particular combinatorics
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
, the necklace splitting problem arises in a variety of contexts including exact division
Exact division
In game theory, an exact or even division is a type of fair division where all the players believe everyone received the same amount.There is no finite fair division procedure for exact division of divisible goods. However there are moving knife procedures for two players...
; its picturesque name is due to mathematicians Noga Alon
Noga Alon
Noga Alon is an Israeli mathematician noted for his contributions to combinatorics and theoretical computer science, having authored hundreds of papers.- Academic background :...
and Douglas B. West.
Suppose a necklace
Necklace
A necklace is an article of jewellery which is worn around the neck. Necklaces are frequently formed from a metal jewellery chain. Others are woven or manufactured from cloth using string or twine....
, open at the clasp, has k ·n beads. There are k · ai beads of colour i, where 1 ≤ i ≤ t. Then the necklace splitting problem is to find a partition of the necklace into k parts (not necessarily contiguous), each of which has exactly ai beads of colour i; such a split is called a k-split. The size of the split is the number of cuts that are needed to separate the parts (the opening at the clasp is not included). Inevitably, one interesting question is to find a split of minimal size.
Alon explains that
-
the problem of finding k-splittings of small size arises naturally when k mathematically oriented thieves steal a necklace with k · ai jewelGemstoneA gemstone or gem is a piece of mineral, which, in cut and polished form, is used to make jewelry or other adornments...
s of type i, and wish to divide it fairly between them, wasting as little as possible of the metal in the links between the jewels.
If the beads of each colour are contiguous on the open necklace, then any k splitting must contain at least k − 1 cuts, so the size is at least (k − 1)t. Alon and West use the Borsuk-Ulam theorem to prove that a k-splitting can always be achieved with this number of cuts. Alon uses these and related ideas to state and prove a generalization of the Hobby–Rice theorem
Hobby–Rice theorem
In mathematics, and in particular the necklace splitting problem, the Hobby–Rice theorem is a result that is useful in establishing the existence of certain solutions. It was proved in 1965 by Charles R. Hobby and John R. Rice; a simplified proof was given in 1976 by A...
.
One cut fewer than needed
In the case of two thieves [i.e. k = 2] and t colours, a fair split would require at most t cuts. If, however, only t − 1 cuts are available, Hungarian mathematician Gábor Simonyi shows that the two thieves can achieve an almost fair division in the following sense.If the necklace is arranged so that no t-split is possible, then for any two subsets D1 and D2 of { 1, 2, ..., t }, not both empty, such that
, a (t − 1)-split exists such that:- If colour
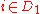, then partition 1 has more beads of colour i than partition 2; - If colour
, then partition 2 has more beads of colour i than partition 1; - If colour i is in neither partition, both partitions have equally many beads of colour i.
I.e. if the thieves have preferences in the form of two "preference" sets D1 and D2, not both empty, there exists a (t − 1)-split so that thief 1 gets more beads of types in his preference set D1 than thief 2; thief 2 gets more beads of types in her preference set D2 than thief 1; and the rest are equal.
Simonyi credits Gábor Tardos with noticing that the result above is a direct generalization of Alon's original necklace theorem in the case k = 2. Either the necklace has a (t − 1)-split, or it does not. If it does, there is nothing to prove. If it does not, we may add beads of a fictitious colour to the necklace, and make D1 consist of the fictitious colour and D2 empty. Then Simonyi's result shows that there is a t-split with equal numbers of each real colour.