Naimark's dilation theorem
Encyclopedia
In operator theory
, Naimark
's dilation theorem is a result that characterizes positive operator valued measures
. It can be viewed as a consequence of Stinespring's dilation theorem
.
Hausdorff space
, H be a Hilbert space
, and L(H) the Banach space
of bounded operator
s on H. A mapping E from the Borel σ-algebra on X to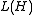
is called a operator-valued measure if it is weakly countably additive, that is, for any disjoint sequence of Borel sets 
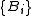, we have
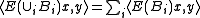
for all x and y. Some terminology for describing such measures are:
is a regular Borel measure, meaning all compact sets have finite total variation and the measure of a set can be approximated by those of open sets.
We will assume throughout that E is regular.
Let C(X) denote the abelian C*-algebra of continuous functions on X. If E is regular and bounded, it induces a map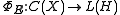
in the obvious way:
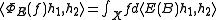
The boundedness of E implies, for all h of unit norm
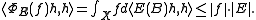
This shows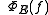
is a bounded operator for all f, and 
itself is a bounded linear map as well.
The properties of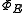
are directly related to those of E:
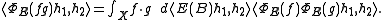
Take f and g to be indicator functions of Borel sets and we see that
is a homomorphism if and only if E is spectral.
The LHS is
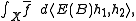
and the RHS is
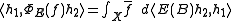
So, for all B,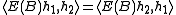
, i.e. E(B) is self adjoint.
, and a self-adjoint, spectral L(K)-valued measure on X, F, such that
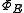and uses Stinespring's dilation theorem
. Since E is positive, so is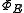
as a map between C*-algebras, as explained above. Furthermore, because the domain of 
, C(X), is an abelian C*-algebra, we have that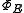 
is completely positive
. By Stinespring's result, there exists a Hilbert space K, a *-homomorphism
, and operator 
such that
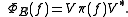
Since π is a *-homomorphism, its corresponding operator-valued measure F is spectral and self adjoint. It is easily seen that F has the desired properties.
Suppose now
, therefore C(X) is the finite dimensional algebra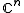 
, and H has finite dimension m. A positive operator-valued measure E then assigns each i a positive semidefinite m X m matrix 
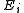. Naimark's theorem now says there
is a projection valued measure on X whose restriction is E.
Of particular interest is the special case when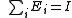
where I is the identity operator. (See the article on POVM
for relevant applications.) This would mean the induced map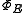
is unital. It can be assumed with no loss of generality that each 
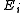is a rank-one projection onto some 
. Under such assumptions, the case 
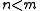is excluded and we must have either:
1)
and E is already a projection valued measure. (Because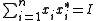 
if and only if 
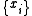is an orthonormal basis.)
,or
2)
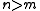and 
does not consist of mutually orthogonal projections.
For the second possibility, the problem of finding a suitable PVM now becomes the following: By assumption, the non-square matrix
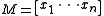
is an isometry, i.e.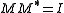
. If we can find a 
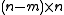matrix N where
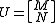
is a n X n unitary matrix, the PVM whose elements are projections onto the column vectors of U will then have the desired properties. In principle, such a N can always be found.
Operator theory
In mathematics, operator theory is the branch of functional analysis that focuses on bounded linear operators, but which includes closed operators and nonlinear operators.Operator theory also includes the study of algebras of operators....
, Naimark
Mark Naimark
Mark Aronovich Naimark was a Soviet mathematician.He was born in Odessa, Russian Empire into a Jewish family and died in Moscow, USSR...
's dilation theorem is a result that characterizes positive operator valued measures
POVM
In functional analysis and quantum measurement theory, a POVM is a measure whose values are non-negative self-adjoint operators on a Hilbert space. It is the most general formulation of a measurement in the theory of quantum physics...
. It can be viewed as a consequence of Stinespring's dilation theorem
Stinespring factorization theorem
In mathematics, Stinespring's dilation theorem, also called Stinespring's factorization theorem, named after W. Forrest Stinespring, is a result from operator theory that represents any completely positive map on a C*-algebra as a composition of two completely positive maps each of which has a...
.
Note
In the mathematical literature, one may also find other results that bear Naimark's name.Some preliminary notions
Let X be a compactCompact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
Hausdorff space
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
, H be a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
, and L(H) the Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
of bounded operator
Bounded operator
In functional analysis, a branch of mathematics, a bounded linear operator is a linear transformation L between normed vector spaces X and Y for which the ratio of the norm of L to that of v is bounded by the same number, over all non-zero vectors v in X...
s on H. A mapping E from the Borel σ-algebra on X to
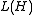is called a operator-valued measure if it is weakly countably additive, that is, for any disjoint sequence of Borel sets 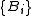, we have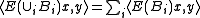for all x and y. Some terminology for describing such measures are:
- E is called regular if the scalar valued measure
is a regular Borel measure, meaning all compact sets have finite total variation and the measure of a set can be approximated by those of open sets.
- E is called bounded if
.
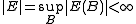- E is called positive if E(B) is a positive operator for all B.
- E is called self-adjoint if E(B) is self-adjoint for all B.
- E is called spectral if
.
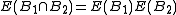We will assume throughout that E is regular.
Let C(X) denote the abelian C*-algebra of continuous functions on X. If E is regular and bounded, it induces a map
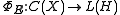in the obvious way: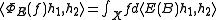The boundedness of E implies, for all h of unit norm
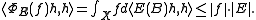
This shows
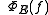is a bounded operator for all f, and itself is a bounded linear map as well.The properties of
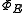are directly related to those of E:- If E is positive, then
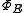, viewed as a map between C*-algebras, is also positive.
-
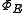is a homomorphism if, by definition, for all continuous f on X and 
,
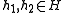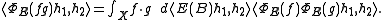
Take f and g to be indicator functions of Borel sets and we see that
is a homomorphism if and only if E is spectral.- Similarly, to say
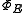respects the * operation means
The LHS is
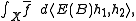
and the RHS is
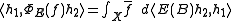
So, for all B,
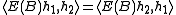, i.e. E(B) is self adjoint.- Combining the previous two facts gives the conclusion that
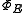is a *-homomorphism if and only if E is spectral and self adjoint. (When E is spectral and self adjoint, E is said to be a projection-valued measureProjection-valued measureIn mathematics, particularly functional analysis a projection-valued measure is a function defined on certain subsets of a fixed set and whose values are self-adjoint projections on a Hilbert space...
or PVM.)
Naimark's theorem
The theorem reads as follows: Let E be a positive L(H)-valued measure on X. There exists a Hilbert space K, a bounded operator, and a self-adjoint, spectral L(K)-valued measure on X, F, such thatProof
We now sketch the proof. The argument passes E to the induced map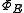 and uses Stinespring's dilation theoremStinespring factorization theorem
In mathematics, Stinespring's dilation theorem, also called Stinespring's factorization theorem, named after W. Forrest Stinespring, is a result from operator theory that represents any completely positive map on a C*-algebra as a composition of two completely positive maps each of which has a...
. Since E is positive, so is
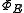as a map between C*-algebras, as explained above. Furthermore, because the domain of , C(X), is an abelian C*-algebra, we have that 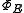is completely positiveChoi's theorem on completely positive maps
In mathematics, Choi's theorem on completely positive maps is a result that classifies completely positive maps between finite-dimensional C*-algebras...
. By Stinespring's result, there exists a Hilbert space K, a *-homomorphism
, and operator such that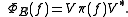Since π is a *-homomorphism, its corresponding operator-valued measure F is spectral and self adjoint. It is easily seen that F has the desired properties.
Finite dimensional case
In the finite dimensional case, there is a somewhat more explicit formulation.Suppose now
, therefore C(X) is the finite dimensional algebra 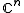, and H has finite dimension m. A positive operator-valued measure E then assigns each i a positive semidefinite m X m matrix 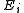. Naimark's theorem now says thereis a projection valued measure on X whose restriction is E.
Of particular interest is the special case when
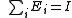where I is the identity operator. (See the article on POVMPOVM
In functional analysis and quantum measurement theory, a POVM is a measure whose values are non-negative self-adjoint operators on a Hilbert space. It is the most general formulation of a measurement in the theory of quantum physics...
for relevant applications.) This would mean the induced map
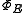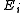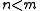is unital. It can be assumed with no loss of generality that each is a rank-one projection onto some . Under such assumptions, the case is excluded and we must have either:1)
and E is already a projection valued measure. (Because 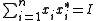if and only if 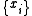is an orthonormal basis.),or
2)
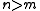and does not consist of mutually orthogonal projections.For the second possibility, the problem of finding a suitable PVM now becomes the following: By assumption, the non-square matrix
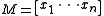
is an isometry, i.e.
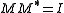. If we can find a 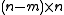matrix N where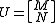is a n X n unitary matrix, the PVM whose elements are projections onto the column vectors of U will then have the desired properties. In principle, such a N can always be found.