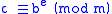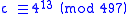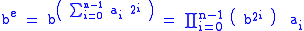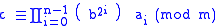Modular exponentiation
Encyclopedia
Modular exponentiation is a type of exponentiation
performed over a modulus
. It is particularly useful in computer science
, especially in the field of cryptography
.
Doing a "modular exponentiation" means calculating the remainder when dividing by a positive integer m (called the modulus) a positive integer b (called the base) raised to the e-th power (e is called the exponent). In other words, problems take the form where given base b, exponent e, and modulus m, one wishes to calculate c such that:
For example, given b = 5, e = 3, and m = 13, the solution c is the remainder of dividing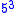
by 13, namely the rest of the division 125 / 13, which works out to be 8.
If b, e, and m are non-negative and b < m, then there exists a unique solution c with the property 0 ≤ c < m.
Modular exponentiation can be performed with a negative exponent e by finding the modular multiplicative inverse d of b modulo m using the extended Euclidean algorithm
. That is:
Modular exponentiation problems similar to the one described above are considered easy to do, even if the numbers involved are enormous. On the other hand, computing the discrete logarithm
(finding e given b, c, and m) is believed to be difficult. This one way function behavior makes modular exponentiation a good candidate for use in cryptographic algorithms.
One could use a calculator to compute 413; this comes out to 67,108,864. Taking this value modulo 497, the answer c is determined to be 445.
Note that b is only one digit in length and that e is only two digits in length, but the value be is 8 digits in length.
In strong cryptography, b is often at least 256 binary digits (77 decimal digits). Consider b = 5 × 1076 and e = 17, both of which are perfectly reasonable values. In this example, b is 77 digits in length and e is 2 digits in length, but the value be is 1309 decimal digits in length. Such calculations are possible on modern computers, but the sheer magnitude of such numbers causes the speed of calculations to slow considerably. As b and e increase even further to provide better security, the value be becomes unwieldy.
The time required to perform the exponentiation depends on the operating environment and the processor. The method described above requires O
(e) multiplications to complete.
This algorithm makes use of the fact that, given two integers a and b, the following two equations are equivalent:
The algorithm is as follows:
Note that in every pass through step 3, the equation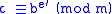
holds true. When step 3 has been executed e times, then, c contains the answer that was sought. In summary, this algorithm basically counts up e′ by ones until e′ reaches e, doing a multiply by b and the modulo operation each time it adds one (to ensure the results stay small).
The example b = 4, e = 13, and m = 497 is presented again. The algorithm passes through step 3 thirteen times:
The final answer for c is therefore 445, as in the first method.
Like the first method, this requires O(e) multiplications to complete. However, since the numbers used in these calculations are much smaller than the numbers used in the first algorithm's calculations, the computation time decreases by a factor of at least O(e) in this method.
In pseudocode, this method can be performed the following way:
function modular_pow(base, exponent, modulus)
c := 1
for e_prime = 1 to exponent
c := (c * base) mod modulus
return c
(also known as binary exponentiation).
First, it is required that the exponent e be converted to binary notation. That is, e can be written as:
In such notation, the length of e is n bits. ai can take the value 0 or 1 for any i such that 0 ≤ i < n - 1. By definition, an - 1 = 1.
The value be can then be written as:
The solution c is therefore:
The following is an example in pseudocode based on Applied Cryptography by Bruce Schneier
. The inputs base, exponent, and modulus correspond to b, e, and m in the equations given above.
function modular_pow(base, exponent, modulus)
result := 1
while exponent > 0
if (exponent & 1) equals 1:
result := (result * base) mod modulus
exponent := exponent >> 1
base = (base * base) mod modulus
return result
Note that upon entering the loop for the first time, the code variable base is equivalent to
. However, the repeated squaring in the third line of code ensures that at the completion of every loop, the variable base is equivalent to 
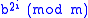, where i is the number of times the loop has been iterated. (This makes i the next working bit of the binary exponent exponent, where the least-significant bit is exponent0).
The first line of code simply carries out the multiplication in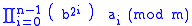
. If ai is zero, no code executes since this effectively multiplies the running total by one. If ai instead is one, the variable base (containing the value 
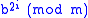of the original base) is simply multiplied in.
Example: base = 4, exponent = 13, and modulus = 497. Note that exponent is 1101 in binary notation. Because exponent is four binary digits in length, the loop executes only four times:
The loop then terminates since exponent is zero, and the result 445 is returned. This agrees with the previous two algorithms.
The running time of this algorithm is O(log exponent). When working with large values of exponent, this offers a substantial speed benefit over both of the previous two algorithms.
Exponentiation
Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
performed over a modulus
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
. It is particularly useful in computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, especially in the field of cryptography
Cryptography
Cryptography is the practice and study of techniques for secure communication in the presence of third parties...
.
Doing a "modular exponentiation" means calculating the remainder when dividing by a positive integer m (called the modulus) a positive integer b (called the base) raised to the e-th power (e is called the exponent). In other words, problems take the form where given base b, exponent e, and modulus m, one wishes to calculate c such that:
For example, given b = 5, e = 3, and m = 13, the solution c is the remainder of dividing
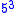by 13, namely the rest of the division 125 / 13, which works out to be 8.If b, e, and m are non-negative and b < m, then there exists a unique solution c with the property 0 ≤ c < m.
Modular exponentiation can be performed with a negative exponent e by finding the modular multiplicative inverse d of b modulo m using the extended Euclidean algorithm
Extended Euclidean algorithm
The extended Euclidean algorithm is an extension to the Euclidean algorithm. Besides finding the greatest common divisor of integers a and b, as the Euclidean algorithm does, it also finds integers x and y that satisfy Bézout's identityThe extended Euclidean algorithm is particularly useful when a...
. That is:
-
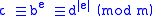where e < 0 and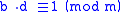 
Modular exponentiation problems similar to the one described above are considered easy to do, even if the numbers involved are enormous. On the other hand, computing the discrete logarithm
Discrete logarithm
In mathematics, specifically in abstract algebra and its applications, discrete logarithms are group-theoretic analogues of ordinary logarithms. In particular, an ordinary logarithm loga is a solution of the equation ax = b over the real or complex numbers...
(finding e given b, c, and m) is believed to be difficult. This one way function behavior makes modular exponentiation a good candidate for use in cryptographic algorithms.
Straightforward method
The most straightforward method of calculating a modular exponent is to calculate be directly, then to take this number modulo m. Consider trying to compute c, given b = 4, e = 13, and m = 497:
One could use a calculator to compute 413; this comes out to 67,108,864. Taking this value modulo 497, the answer c is determined to be 445.
Note that b is only one digit in length and that e is only two digits in length, but the value be is 8 digits in length.
In strong cryptography, b is often at least 256 binary digits (77 decimal digits). Consider b = 5 × 1076 and e = 17, both of which are perfectly reasonable values. In this example, b is 77 digits in length and e is 2 digits in length, but the value be is 1309 decimal digits in length. Such calculations are possible on modern computers, but the sheer magnitude of such numbers causes the speed of calculations to slow considerably. As b and e increase even further to provide better security, the value be becomes unwieldy.
The time required to perform the exponentiation depends on the operating environment and the processor. The method described above requires O
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
(e) multiplications to complete.
Memory-efficient method
A second method to compute modular exponentiation requires more operations than the first method. Because the required memory is substantially less, however, operations take less time than before. The end result is that the algorithm is faster.This algorithm makes use of the fact that, given two integers a and b, the following two equations are equivalent:
The algorithm is as follows:
- Set c = 1, e′ = 0.
- Increase e′ by 1.
- Set
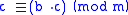. - If e′ < e, goto step 2. Else, c contains the correct solution to
.
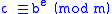Note that in every pass through step 3, the equation
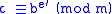holds true. When step 3 has been executed e times, then, c contains the answer that was sought. In summary, this algorithm basically counts up e′ by ones until e′ reaches e, doing a multiply by b and the modulo operation each time it adds one (to ensure the results stay small).The example b = 4, e = 13, and m = 497 is presented again. The algorithm passes through step 3 thirteen times:
- e′ = 1. c = (1 * 4) mod 497 = 4 mod 497 = 4.
- e′ = 2. c = (4 * 4) mod 497 = 16 mod 497 = 16.
- e′ = 3. c = (16 * 4) mod 497 = 64 mod 497 = 64.
- e′ = 4. c = (64 * 4) mod 497 = 256 mod 497 = 256.
- e′ = 5. c = (256 * 4) mod 497 = 1024 mod 497 = 30.
- e′ = 6. c = (30 * 4) mod 497 = 120 mod 497 = 120.
- e′ = 7. c = (120 * 4) mod 497 = 480 mod 497 = 480.
- e′ = 8. c = (480 * 4) mod 497 = 1920 mod 497 = 429.
- e′ = 9. c = (429 * 4) mod 497 = 1716 mod 497 = 225.
- e′ = 10. c = (225 * 4) mod 497 = 900 mod 497 = 403.
- e′ = 11. c = (403 * 4) mod 497 = 1612 mod 497 = 121.
- e′ = 12. c = (121 * 4) mod 497 = 484 mod 497 = 484.
- e′ = 13. c = (484 * 4) mod 497 = 1936 mod 497 = 445.
The final answer for c is therefore 445, as in the first method.
Like the first method, this requires O(e) multiplications to complete. However, since the numbers used in these calculations are much smaller than the numbers used in the first algorithm's calculations, the computation time decreases by a factor of at least O(e) in this method.
In pseudocode, this method can be performed the following way:
function modular_pow(base, exponent, modulus)
c := 1
for e_prime = 1 to exponent
c := (c * base) mod modulus
return c
Right-to-left binary method
A third method drastically reduces both the number of operations and the memory footprint required to perform modular exponentiation. It is a combination of the previous method and a more general principle called exponentiation by squaringExponentiation by squaring
Exponentiating by squaring is a general method for fast computation of large integer powers of a number. Some variants are commonly referred to as square-and-multiply algorithms or binary exponentiation. In additive notation the appropriate term is double-and-add...
(also known as binary exponentiation).
First, it is required that the exponent e be converted to binary notation. That is, e can be written as:
In such notation, the length of e is n bits. ai can take the value 0 or 1 for any i such that 0 ≤ i < n - 1. By definition, an - 1 = 1.
The value be can then be written as:
The solution c is therefore:
The following is an example in pseudocode based on Applied Cryptography by Bruce Schneier
Bruce Schneier
Bruce Schneier is an American cryptographer, computer security specialist, and writer. He is the author of several books on general security topics, computer security and cryptography, and is the founder and chief technology officer of BT Managed Security Solutions, formerly Counterpane Internet...
. The inputs base, exponent, and modulus correspond to b, e, and m in the equations given above.
function modular_pow(base, exponent, modulus)
result := 1
while exponent > 0
if (exponent & 1) equals 1:
result := (result * base) mod modulus
exponent := exponent >> 1
base = (base * base) mod modulus
return result
Note that upon entering the loop for the first time, the code variable base is equivalent to
. However, the repeated squaring in the third line of code ensures that at the completion of every loop, the variable base is equivalent to 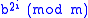, where i is the number of times the loop has been iterated. (This makes i the next working bit of the binary exponent exponent, where the least-significant bit is exponent0).The first line of code simply carries out the multiplication in
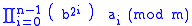. If ai is zero, no code executes since this effectively multiplies the running total by one. If ai instead is one, the variable base (containing the value 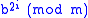of the original base) is simply multiplied in.Example: base = 4, exponent = 13, and modulus = 497. Note that exponent is 1101 in binary notation. Because exponent is four binary digits in length, the loop executes only four times:
- Upon entering the loop for the first time, variables base = 4, exponent = 1101 (binary), and result = 1. Because the right-most bit of exponent is 1, result is changed to be (1 * 4) % 497, or 4. exponent is right-shifted to become 110 (binary), and base is squared to be (4 * 4) % 497, or 16.
- The second time through the loop, the right-most bit of exponent is 0, causing result to retain its present value of 4. exponent is right-shifted to become 11 (binary), and base is squared to be (16 * 16) % 497, or 256.
- The third time through the loop, the right-most bit of e is 1. result is changed to be (4 * 256) % 497, or 30. exponent is right-shifted to become 1, and base is squared to be (256 * 256) % 497, or 429.
- The fourth time through the loop, the right-most bit of exponent is 1. result is changed to be (30 * 429) % 497, or 445. exponent is right-shifted to become 0, and base is squared to be (429 * 429) % 497, or 151.
The loop then terminates since exponent is zero, and the result 445 is returned. This agrees with the previous two algorithms.
The running time of this algorithm is O(log exponent). When working with large values of exponent, this offers a substantial speed benefit over both of the previous two algorithms.
External links
- Fast Modular Exponentiation Java Applet - University of MinnesotaUniversity of MinnesotaThe University of Minnesota, Twin Cities is a public research university located in Minneapolis and St. Paul, Minnesota, United States. It is the oldest and largest part of the University of Minnesota system and has the fourth-largest main campus student body in the United States, with 52,557...
Math Department