
Menger sponge
Encyclopedia
In mathematics
, the Menger sponge is a fractal
curve. It is a universal curve, in that it has topological dimension one, and any other curve
(more precisely: any compact metric space of topological dimension 1) is homeomorphic to some subset of it. It is sometimes called the Menger-Sierpinski sponge or the Sierpinski sponge. It is a three-dimensional extension of the Cantor set
and Sierpinski carpet
. It was first described by while exploring the concept of topological dimension.
The Menger sponge simultaneously exhibits an infinite surface area and encloses zero volume.
The second iteration will give you a level-2 sponge (third image), the third iteration gives a level-3 sponge (fourth image), and so on. The Menger sponge itself is the limit of this process after an infinite number of iterations.
The number of cubes is 20n, with n being the number of iterations performed on the first cube.
; furthermore, any intersection of the Menger sponge with a diagonal or medium of the initial cube M0 is a Cantor set
.
The Menger sponge is a closed set
; since it is also bounded, the Heine–Borel theorem implies that it is compact. It has Lebesgue measure
0. It is an uncountable set
.
The topological dimension of the Menger sponge is one, the same as any curve
. Menger showed, in the 1926 construction, that the sponge is a universal curve, in that any possible one-dimensional curve is homeomorphic to a subset of the Menger sponge, where here a curve means any compact
metric space
of Lebesgue covering dimension
one; this includes trees
and graphs
with an arbitrary countable number of edges, vertices and closed loops, connected in arbitrary ways. In a similar way, the Sierpinski carpet
is a universal curve for all curves that can be drawn on the two-dimensional plane. The Menger sponge constructed in three dimensions extends this idea to graphs that are not planar
, and might be embedded in any number of dimensions.
The Menger sponge simultaneously exhibits an infinite surface area and encloses zero volume. In spite of this, there exists a homeomorphism of the cube having finite distortion
that "squeezes the sponge" in the sense that the holes in the sponge go to a Cantor set of zero measure .
The sponge has a Hausdorff dimension
of (log 20) / (log 3) (approximately 2.726833).

where M0 is the unit cube
and
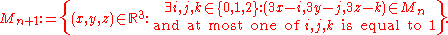
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Menger sponge is a fractal
Fractal
A fractal has been defined as "a rough or fragmented geometric shape that can be split into parts, each of which is a reduced-size copy of the whole," a property called self-similarity...
curve. It is a universal curve, in that it has topological dimension one, and any other curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
(more precisely: any compact metric space of topological dimension 1) is homeomorphic to some subset of it. It is sometimes called the Menger-Sierpinski sponge or the Sierpinski sponge. It is a three-dimensional extension of the Cantor set
Cantor set
In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of remarkable and deep properties. It was discovered in 1875 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883....
and Sierpinski carpet
Sierpinski carpet
The Sierpinski carpet is a plane fractal first described by Wacław Sierpiński in 1916. The carpet is a generalization of the Cantor set to two dimensions . Sierpiński demonstrated that this fractal is a universal curve, in that any possible one-dimensional graph, projected onto the two-dimensional...
. It was first described by while exploring the concept of topological dimension.
The Menger sponge simultaneously exhibits an infinite surface area and encloses zero volume.
Construction
The construction of a Menger sponge can be described as follows:- Begin with a cube (first image).
- Divide every face of the cube into 9 squares, like a Rubik's CubeRubik's CubeRubik's Cube is a 3-D mechanical puzzle invented in 1974 by Hungarian sculptor and professor of architecture Ernő Rubik.Originally called the "Magic Cube", the puzzle was licensed by Rubik to be sold by Ideal Toy Corp. in 1980 and won the German Game of the Year special award for Best Puzzle that...
. This will sub-divide the cube into 27 smaller cubes. - Remove the smaller cube in the middle of each face, and remove the smaller cube in the very center of the larger cube, leaving 20 smaller cubes (second image). This is a level-1 Menger sponge (resembling a Void CubeVoid CubeThe Void Cube is a 3-D mechanical puzzle similar to a Rubik's Cube, with the notable difference being that the center "cubes" are missing, which causes the puzzle to resemble a level 1 Menger sponge. The central "spider" used on the Rubik's Cube is also absent, creating holes straight through the...
). - Repeat steps 2 and 3 for each of the remaining smaller cubes, and continue to iterate ad infinitum.
The second iteration will give you a level-2 sponge (third image), the third iteration gives a level-3 sponge (fourth image), and so on. The Menger sponge itself is the limit of this process after an infinite number of iterations.
The number of cubes is 20n, with n being the number of iterations performed on the first cube.
Properties
Each face of the Menger sponge is a Sierpinski carpetSierpinski carpet
The Sierpinski carpet is a plane fractal first described by Wacław Sierpiński in 1916. The carpet is a generalization of the Cantor set to two dimensions . Sierpiński demonstrated that this fractal is a universal curve, in that any possible one-dimensional graph, projected onto the two-dimensional...
; furthermore, any intersection of the Menger sponge with a diagonal or medium of the initial cube M0 is a Cantor set
Cantor set
In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of remarkable and deep properties. It was discovered in 1875 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883....
.
The Menger sponge is a closed set
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
; since it is also bounded, the Heine–Borel theorem implies that it is compact. It has Lebesgue measure
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
0. It is an uncountable set
Uncountable set
In mathematics, an uncountable set is an infinite set that contains too many elements to be countable. The uncountability of a set is closely related to its cardinal number: a set is uncountable if its cardinal number is larger than that of the set of all natural numbers.-Characterizations:There...
.
The topological dimension of the Menger sponge is one, the same as any curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
. Menger showed, in the 1926 construction, that the sponge is a universal curve, in that any possible one-dimensional curve is homeomorphic to a subset of the Menger sponge, where here a curve means any compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
of Lebesgue covering dimension
Lebesgue covering dimension
Lebesgue covering dimension or topological dimension is one of several inequivalent notions of assigning a topological invariant dimension to a given topological space.-Definition:...
one; this includes trees
Tree (graph theory)
In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...
and graphs
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
with an arbitrary countable number of edges, vertices and closed loops, connected in arbitrary ways. In a similar way, the Sierpinski carpet
Sierpinski carpet
The Sierpinski carpet is a plane fractal first described by Wacław Sierpiński in 1916. The carpet is a generalization of the Cantor set to two dimensions . Sierpiński demonstrated that this fractal is a universal curve, in that any possible one-dimensional graph, projected onto the two-dimensional...
is a universal curve for all curves that can be drawn on the two-dimensional plane. The Menger sponge constructed in three dimensions extends this idea to graphs that are not planar
Planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
, and might be embedded in any number of dimensions.
The Menger sponge simultaneously exhibits an infinite surface area and encloses zero volume. In spite of this, there exists a homeomorphism of the cube having finite distortion
Distortion (mathematics)
In mathematics, the distortion is a measure of the amount by which a function from the Euclidean plane to itself distorts circles to ellipses. If the distortion of a function is equal to one, then it is conformal; if the distortion is bounded and the function is a homeomorphism, then it is...
that "squeezes the sponge" in the sense that the holes in the sponge go to a Cantor set of zero measure .
The sponge has a Hausdorff dimension
Hausdorff dimension
thumb|450px|Estimating the Hausdorff dimension of the coast of Great BritainIn mathematics, the Hausdorff dimension is an extended non-negative real number associated with any metric space. The Hausdorff dimension generalizes the notion of the dimension of a real vector space...
of (log 20) / (log 3) (approximately 2.726833).
Formal definition
Formally, a Menger sponge can be defined as follows:
where M0 is the unit cube
Unit cube
A unit cube, sometimes called a cube of side 1, is a cube whose sides are 1 unit long. The volume of a 3-dimensional unit cube is 1 cubic unit, and its total surface area is 6 square units.- Unit Hypercube :...
and
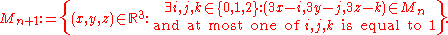
See also
- List of fractals by Hausdorff dimension
- Sierpiński triangleSierpinski triangleThe Sierpinski triangle , also called the Sierpinski gasket or the Sierpinski Sieve, is a fractal and attractive fixed set named after the Polish mathematician Wacław Sierpiński who described it in 1915. However, similar patterns appear already in the 13th-century Cosmati mosaics in the cathedral...
- Sierpiński tetrahedron
- Koch snowflakeKoch snowflakeThe Koch snowflake is a mathematical curve and one of the earliest fractal curves to have been described...
- Apollonian gasketApollonian gasketIn mathematics, an Apollonian gasket or Apollonian net is a fractal generated from triples of circles, where each circle is tangent to the other two. It is named after Greek mathematician Apollonius of Perga.-Construction:...
External links
- Menger sponge at Wolfram MathWorld
- An interactive Menger sponge
- Fractal polyhedra (VRML) and interactive Java models
- Puzzle Hunt — Video explaining Zeno's paradoxes using Menger-Sierpinski sponge
- The Business Card Menger Sponge Project
- Menger Sponge Assembly Construction of a Level-3 Menger Sponge from business cards
- Menger Sponge Animations — Menger sponge animations up to level 9, discussion of optimization for 3d.
- L3 Menger Sponge with business cards 2006 – An L3 Menger sponge by students at Cornell College built in 2006
- Level 3 Menger Sponge made of Business Cards – A level-3 Menger sponge built by students at Mississippi State University out of 48,000 folded business cards.
- Menger sphere, rendered in SunFlowSunflowSunflow is an open source global illumination rendering system written in Java.The current status of the project is unknown, but the last announcement on the program's official page was made in 2007.-External links:***...
- Post-It Menger Sponge – a level 3 Menger sponge being built from Post-its
- The Mystery of the Menger Sponge. Sliced diagonally to reveal stars.

