
Leopoldt's conjecture
Encyclopedia
In algebraic number theory
, Leopoldt's conjecture, introduced by , states that p-adic regulator of a number field does not vanish. The p-adic regulator is an analogue of the usual
regulator defined using p-adic logarithms instead of the usual logarithms, introduced by .
Leopoldt proposed a definition of a p-adic regulator Rp attached to K and a prime number p. The definition of Rp uses an appropriate determinant with entries the p-adic logarithm of a generating set of units of K (up to torsion), in the manner of the usual regulator. The conjecture, which for general K is still open , then comes out as the statement that Rp is not zero.
P of K above some fixed rational prime p, let UP denote the local units at P and let U1,P denote the subgroup of principal units in UP. Set
Then let E1 denote the set of global units ε that map to U1 via the diagonal embedding of the global units in E.
Since is a finite-index
is a finite-index
subgroup of the global units, it is an abelian group
of rank , where
, where  is the number of real embeddings of
is the number of real embeddings of 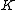 and
and 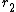 the number of pairs of complex embeddings. Leopoldt's conjecture states that the
the number of pairs of complex embeddings. Leopoldt's conjecture states that the  -module rank of the closure of
-module rank of the closure of 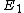 embedded diagonally in
embedded diagonally in  is also
is also 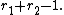
Leopoldt's conjecture is known in the special case where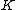 is an abelian extension
is an abelian extension
of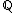 or an abelian extension of an imaginary quadratic number field
or an abelian extension of an imaginary quadratic number field
: reduced the abelian case to a p-adic version of Baker's theorem
, which was proved shortly afterwards by .
has announced a proof of Leopoldt's conjecture for all number fields.
expressed the residue of the p-adic Dedekind zeta function of a totally real field at s = 1 in terms of the p-adic regulator. As a consequence, Leopoldt's conjecture for those fields is equivalent to their p-adic Dedekind zeta functions having a simple pole at s = 1.
Algebraic number theory
Algebraic number theory is a major branch of number theory which studies algebraic structures related to algebraic integers. This is generally accomplished by considering a ring of algebraic integers O in an algebraic number field K/Q, and studying their algebraic properties such as factorization,...
, Leopoldt's conjecture, introduced by , states that p-adic regulator of a number field does not vanish. The p-adic regulator is an analogue of the usual
regulator defined using p-adic logarithms instead of the usual logarithms, introduced by .
Leopoldt proposed a definition of a p-adic regulator Rp attached to K and a prime number p. The definition of Rp uses an appropriate determinant with entries the p-adic logarithm of a generating set of units of K (up to torsion), in the manner of the usual regulator. The conjecture, which for general K is still open , then comes out as the statement that Rp is not zero.
Formulation
Let K be a number field and for each primePrime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
P of K above some fixed rational prime p, let UP denote the local units at P and let U1,P denote the subgroup of principal units in UP. Set
Then let E1 denote the set of global units ε that map to U1 via the diagonal embedding of the global units in E.
Since
 is a finite-index
is a finite-indexIndex of a subgroup
In mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...
subgroup of the global units, it is an abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
of rank
 , where
, where  is the number of real embeddings of
is the number of real embeddings of 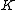 and
and 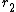 the number of pairs of complex embeddings. Leopoldt's conjecture states that the
the number of pairs of complex embeddings. Leopoldt's conjecture states that the  -module rank of the closure of
-module rank of the closure of 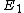 embedded diagonally in
embedded diagonally in  is also
is also 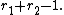
Leopoldt's conjecture is known in the special case where
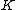 is an abelian extension
is an abelian extensionAbelian extension
In abstract algebra, an abelian extension is a Galois extension whose Galois group is abelian. When the Galois group is a cyclic group, we have a cyclic extension. More generally, a Galois extension is called solvable if its Galois group is solvable....
of
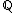 or an abelian extension of an imaginary quadratic number field
or an abelian extension of an imaginary quadratic number fieldQuadratic field
In algebraic number theory, a quadratic field is an algebraic number field K of degree two over Q. It is easy to show that the map d ↦ Q is a bijection from the set of all square-free integers d ≠ 0, 1 to the set of all quadratic fields...
: reduced the abelian case to a p-adic version of Baker's theorem
Baker's theorem
In transcendence theory, a mathematical discipline, Baker's theorem gives a lower bound for linear combinations of logarithms of algebraic numbers...
, which was proved shortly afterwards by .
has announced a proof of Leopoldt's conjecture for all number fields.
expressed the residue of the p-adic Dedekind zeta function of a totally real field at s = 1 in terms of the p-adic regulator. As a consequence, Leopoldt's conjecture for those fields is equivalent to their p-adic Dedekind zeta functions having a simple pole at s = 1.


