
Lattice sieving
Encyclopedia
Lattice sieving is a technique for finding smooth
values of a bivariate polynomial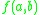 over a large region. It is almost exclusively used in conjunction with the number field sieve. The original idea of the lattice sieve came from John Pollard
over a large region. It is almost exclusively used in conjunction with the number field sieve. The original idea of the lattice sieve came from John Pollard
.
The algorithm implicitly involves the ideal
structure of the number field of the polynomial; it takes advantage of the theorem that any prime ideal
above some rational prime p can be written as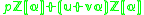 . One then picks many prime numbers q of an appropriate size, usually just above the factor base
. One then picks many prime numbers q of an appropriate size, usually just above the factor base
limit, and proceeds by
For the number field sieve application, it is necessary for two polynomials both to have smooth values; this is handled by running the inner loop over both polynomials, whilst the special-q can be taken from either side.
Smooth number
In number theory, a smooth number is an integer which factors completely into small prime numbers. The term seems to have been coined by Leonard Adleman. Smooth numbers are especially important in cryptography relying on factorization.-Definition:...
values of a bivariate polynomial
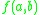 over a large region. It is almost exclusively used in conjunction with the number field sieve. The original idea of the lattice sieve came from John Pollard
over a large region. It is almost exclusively used in conjunction with the number field sieve. The original idea of the lattice sieve came from John PollardJohn Pollard (mathematician)
John M. Pollard is a British mathematician who has invented algorithms for the factorization of large numbers and for the calculation of discrete logarithms....
.
The algorithm implicitly involves the ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
structure of the number field of the polynomial; it takes advantage of the theorem that any prime ideal
Prime ideal
In algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
above some rational prime p can be written as
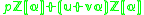 . One then picks many prime numbers q of an appropriate size, usually just above the factor base
. One then picks many prime numbers q of an appropriate size, usually just above the factor baseFactor base
In computational number theory, the factor base is a mathematical tool commonly used in algorithms involving extensive sieving of potential factors.-Usage:...
limit, and proceeds by
-
- For each q, list the prime ideals above q by factorising the polynomial f(a,b) over
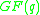
- For each of these prime ideals, which are called 'special
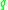 's, construct a reduced basisLattice reductionIn mathematics, the goal of lattice basis reduction is given an integer lattice basis as input, to find a basis with short, nearly orthogonal vectors. This is realized using different algorithms, whose running time is usually at least exponential in the dimension of the lattice.-Nearly...
's, construct a reduced basisLattice reductionIn mathematics, the goal of lattice basis reduction is given an integer lattice basis as input, to find a basis with short, nearly orthogonal vectors. This is realized using different algorithms, whose running time is usually at least exponential in the dimension of the lattice.-Nearly...
 for the lattice L generated by
for the lattice L generated by 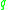 ; set a two-dimensional array called the sieve region to zero.
; set a two-dimensional array called the sieve region to zero.
- For each prime ideal
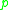 in the factor base, construct a reduced basis
in the factor base, construct a reduced basis  for the sublattice of L generated by
for the sublattice of L generated by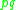
- For each element of that sublattice lying within a sufficiently large sieve region, add
 to that entry.
to that entry.
- For each element of that sublattice lying within a sufficiently large sieve region, add
- For each prime ideal
- Read out all the entries in the sieve region with a large enough value
- For each of these prime ideals, which are called 'special
- For each q, list the prime ideals above q by factorising the polynomial f(a,b) over
For the number field sieve application, it is necessary for two polynomials both to have smooth values; this is handled by running the inner loop over both polynomials, whilst the special-q can be taken from either side.

