Krull's theorem
Encyclopedia
In mathematics
, more specifically in ring theory
, Krull's theorem, named after Wolfgang Krull
, proves the existence of maximal ideal
s in any unital ring
. The theorem was first stated in 1929 and is equivalent to the axiom of choice.
, which is not the trivial ring. Then R contains a maximal ideal.
The statement can be proved using Zorn's lemma, which is equivalent to the axiom of choice.
A slightly stronger (but equivalent) result, which can be proved in a similar fashion, is as follows: Let R be a unital ring which is not the trivial ring, and let I be a proper ideal of R. Then there is a maximal ideal of R containing I. Note that this result does indeed imply the previous theorem, by taking I to be the zero ideal (0). To prove the statement, consider the set S of all proper ideals of R containing I. S is certainly nonempty as I is an element of S. Furthermore, for any chain T of S, it is easy to see that union of ideals in T is an ideal J. In fact, J is proper (otherwise 1 ∈ J implying that 1 ∈ N for some N ∈ T contradicting that T ⊂ S). Therefore by Zorn's lemma, S has a maximal element which must be a maximal ideal containing I.
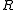be a Noetherian ring and 
an element of 
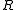which is neither a zero divisor
nor a unit
. Then every minimal prime ideal
containing 
has height 1.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, more specifically in ring theory
Ring theory
In abstract algebra, ring theory is the study of rings—algebraic structures in which addition and multiplication are defined and have similar properties to those familiar from the integers...
, Krull's theorem, named after Wolfgang Krull
Wolfgang Krull
Wolfgang Krull was a German mathematician working in the field of commutative algebra.He was born in Baden-Baden, Imperial Germany and died in Bonn, West Germany.- See also :* Krull dimension* Krull topology...
, proves the existence of maximal ideal
Maximal ideal
In mathematics, more specifically in ring theory, a maximal ideal is an ideal which is maximal amongst all proper ideals. In other words, I is a maximal ideal of a ring R if I is an ideal of R, I ≠ R, and whenever J is another ideal containing I as a subset, then either J = I or J = R...
s in any unital ring
Ring
Ring may refer to:*Ring , a decorative ornament worn on fingers, toes, or around the arm or neck-Computing:* Ring , a layer of protection in computer systems...
. The theorem was first stated in 1929 and is equivalent to the axiom of choice.
Krull's theorem
Let R be a unital ringRing
Ring may refer to:*Ring , a decorative ornament worn on fingers, toes, or around the arm or neck-Computing:* Ring , a layer of protection in computer systems...
, which is not the trivial ring. Then R contains a maximal ideal.
The statement can be proved using Zorn's lemma, which is equivalent to the axiom of choice.
A slightly stronger (but equivalent) result, which can be proved in a similar fashion, is as follows: Let R be a unital ring which is not the trivial ring, and let I be a proper ideal of R. Then there is a maximal ideal of R containing I. Note that this result does indeed imply the previous theorem, by taking I to be the zero ideal (0). To prove the statement, consider the set S of all proper ideals of R containing I. S is certainly nonempty as I is an element of S. Furthermore, for any chain T of S, it is easy to see that union of ideals in T is an ideal J. In fact, J is proper (otherwise 1 ∈ J implying that 1 ∈ N for some N ∈ T contradicting that T ⊂ S). Therefore by Zorn's lemma, S has a maximal element which must be a maximal ideal containing I.
Krull's Hauptidealsatz
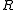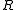Another theorem commonly referred to as Krull's theorem: Let be a Noetherian ring and an element of which is neither a zero divisorZero divisor
In abstract algebra, a nonzero element a of a ring is a left zero divisor if there exists a nonzero b such that ab = 0. Similarly, a nonzero element a of a ring is a right zero divisor if there exists a nonzero c such that ca = 0. An element that is both a left and a right zero divisor is simply...
nor a unit
Unit (ring theory)
In mathematics, an invertible element or a unit in a ring R refers to any element u that has an inverse element in the multiplicative monoid of R, i.e. such element v that...
. Then every minimal prime ideal
Prime ideal
In algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
containing has height 1.