
Jónsson cardinal
Encyclopedia
In set theory
, a Jónsson cardinal (named after Bjarni Jónsson
) is a certain kind of large cardinal number.
An uncountable
cardinal number
κ is said to be Jónsson if for every function f: [κ]<ω → κ there is a set H of order type κ such that for each n, f restricted to n-element subsets of H omits at least one value in κ.
Every Rowbottom cardinal
is Jónsson. By a theorem of Eugene M. Kleinberg, the theories ZFC + “there is a Rowbottom cardinal
” and ZFC + “there is a Jónsson cardinal” are equiconsistent. William Mitchell proved, with the help of the Dodd-Jensen core model
that the consistency of the existence of a Jónsson cardinal implies the consistency of the existence of a Ramsey cardinal
.
In general, Jónsson cardinals need not be large cardinals in the usual sense: they can be singular. But the existence of a singular Jónsson cardinal is equiconsistent to the existence of a measurable cardinal
. Using the axiom of choice, a lot of small cardinals (the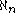 , for instance) can be proved to be not Jónsson. Results like this need the axiom of choice, however: The axiom of determinacy
, for instance) can be proved to be not Jónsson. Results like this need the axiom of choice, however: The axiom of determinacy
does imply that for every positive natural number n, the cardinal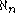 is Jónsson.
is Jónsson.
A Jónsson algebra is an algebra with no proper subalgebras of the same cardinality. (Here an algebra means
a model for a language with a countable number of function symbols, in other words a set with a countable number of functions from finite products of the set to itself.) A cardinal is a Jónsson cardinal if and only if there are no Jónsson algebras of that cardinality. The existence of Jónsson function
s shows that if algebras are allowed to have infinitary operations, then there are no analogues of Jónsson cardinals.
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, a Jónsson cardinal (named after Bjarni Jónsson
Bjarni Jónsson
Bjarni Jónsson is an Icelandic mathematician and logician working in universal algebra and lattice theory. He is emeritus Distinguished Professor of Mathematics at Vanderbilt University and the honorary editor in chief of Algebra Universalis...
) is a certain kind of large cardinal number.
An uncountable
Uncountable set
In mathematics, an uncountable set is an infinite set that contains too many elements to be countable. The uncountability of a set is closely related to its cardinal number: a set is uncountable if its cardinal number is larger than that of the set of all natural numbers.-Characterizations:There...
cardinal number
Cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
κ is said to be Jónsson if for every function f: [κ]<ω → κ there is a set H of order type κ such that for each n, f restricted to n-element subsets of H omits at least one value in κ.
Every Rowbottom cardinal
Rowbottom cardinal
In set theory, a Rowbottom cardinal, introduced by , is a certain kind of large cardinal number.An uncountable cardinal number κ is said to be Rowbottom if for every function f: [κ]...
is Jónsson. By a theorem of Eugene M. Kleinberg, the theories ZFC + “there is a Rowbottom cardinal
Rowbottom cardinal
In set theory, a Rowbottom cardinal, introduced by , is a certain kind of large cardinal number.An uncountable cardinal number κ is said to be Rowbottom if for every function f: [κ]...
” and ZFC + “there is a Jónsson cardinal” are equiconsistent. William Mitchell proved, with the help of the Dodd-Jensen core model
Core model
In set theory, the core model is a definable inner model of the universe of all sets. Even though set theorists refer to "the core model", it is not a uniquely identified mathematical object. Rather, it is a class of inner models that under the right set theoretic assumptions have very special...
that the consistency of the existence of a Jónsson cardinal implies the consistency of the existence of a Ramsey cardinal
Ramsey cardinal
In mathematics, a Ramsey cardinal is a certain kind of large cardinal number introduced by and named after Frank P. Ramsey.With [κ]<ω denoting the set of all finite subsets of κ, a cardinal number κ such that for every function...
.
In general, Jónsson cardinals need not be large cardinals in the usual sense: they can be singular. But the existence of a singular Jónsson cardinal is equiconsistent to the existence of a measurable cardinal
Measurable cardinal
- Measurable :Formally, a measurable cardinal is an uncountable cardinal number κ such that there exists a κ-additive, non-trivial, 0-1-valued measure on the power set of κ...
. Using the axiom of choice, a lot of small cardinals (the
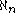 , for instance) can be proved to be not Jónsson. Results like this need the axiom of choice, however: The axiom of determinacy
, for instance) can be proved to be not Jónsson. Results like this need the axiom of choice, however: The axiom of determinacyAxiom of determinacy
The axiom of determinacy is a possible axiom for set theory introduced by Jan Mycielski and Hugo Steinhaus in 1962. It refers to certain two-person games of length ω with perfect information...
does imply that for every positive natural number n, the cardinal
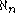 is Jónsson.
is Jónsson.A Jónsson algebra is an algebra with no proper subalgebras of the same cardinality. (Here an algebra means
a model for a language with a countable number of function symbols, in other words a set with a countable number of functions from finite products of the set to itself.) A cardinal is a Jónsson cardinal if and only if there are no Jónsson algebras of that cardinality. The existence of Jónsson function
Jónsson function
In set theory, a mathematical discipline, an ω-Jónsson function, named for Bjarni Jónsson, for a set of ordinals x is a function from [x]^\omega to x such that for any subset y of x with the same cardinality as x, f restricted to [y]^\omega maps onto x...
s shows that if algebras are allowed to have infinitary operations, then there are no analogues of Jónsson cardinals.

