
Justesen code
Encyclopedia
Introduction
In coding theoryCoding theory
Coding theory is the study of the properties of codes and their fitness for a specific application. Codes are used for data compression, cryptography, error-correction and more recently also for network coding...
, Justesen codes form a class of Error detection and correction codes
Error detection and correction
In information theory and coding theory with applications in computer science and telecommunication, error detection and correction or error control are techniques that enable reliable delivery of digital data over unreliable communication channels...
which are derived from Reed-Solomon code
Reed–Solomon error correction
In coding theory, Reed–Solomon codes are non-binary cyclic error-correcting codes invented by Irving S. Reed and Gustave Solomon. They described a systematic way of building codes that could detect and correct multiple random symbol errors...
and have good error-control properties. In code concatenation, we compose an outer code
 with an inner code
with an inner code 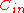 . By using the appropriate outer and inner code
. By using the appropriate outer and inner code  and
and 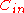 , we can obtain new bound for code, such as Zyablov bound
, we can obtain new bound for code, such as Zyablov boundZyablov bound
In coding theory, the Zyablov bound, is a lower bound on the rate R and relative distance \delta of the concatenated codes.-Statement of the bound:...
. The Justesen code composes the Reed-Solomon code
Reed–Solomon error correction
In coding theory, Reed–Solomon codes are non-binary cyclic error-correcting codes invented by Irving S. Reed and Gustave Solomon. They described a systematic way of building codes that could detect and correct multiple random symbol errors...
with the Wonzencraft ensemble and has a strongly explicit construction.Loosely speaking, the code has the strongly explicit construction if we can construct it in log space complexity. Unlike the usual code concatenation, the Justesen code obtains the power by using different linear inner codes as we see below.
Definition
Justesen code is concatenation code with different linear inner codes, which is composed of an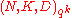 outer code
outer code  and different
and different 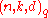 inner codes
inner codes 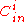 ,
, 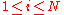 . More precisely, the concatenation of these codes, denoted by
. More precisely, the concatenation of these codes, denoted by 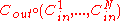 , is defined as follows. Given a message
, is defined as follows. Given a message 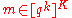 , we compute the codeword produced by an outer code
, we compute the codeword produced by an outer code  :
: 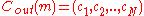 . Then we apply each code of N linear inner codes to each coordinate of that codeword to produce the final codeword; that is,
. Then we apply each code of N linear inner codes to each coordinate of that codeword to produce the final codeword; that is, 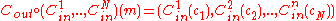 . Look back to the definition of the outer code and linear inner codes, this definition of the Justesen code makes sense because the codeword of the outer code is a vector with
. Look back to the definition of the outer code and linear inner codes, this definition of the Justesen code makes sense because the codeword of the outer code is a vector with  elements, and we have
elements, and we have  linear inner codes to apply for those
linear inner codes to apply for those  elements.
elements.Here for the Justesen code, the outer code
 is chosen to be Reed Solomon code
is chosen to be Reed Solomon codeReed–Solomon error correction
In coding theory, Reed–Solomon codes are non-binary cyclic error-correcting codes invented by Irving S. Reed and Gustave Solomon. They described a systematic way of building codes that could detect and correct multiple random symbol errors...
over a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
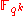 evaluated over
evaluated over 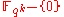 of rate
of rateCode rate
In telecommunication and information theory, the code rate of a forward error correction code is the proportion of the data-stream that is useful...
 ,
,  <
<  <
< 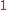 . The outer code
. The outer code  have the relative distance
have the relative distance  and block length of
and block length of 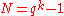 . The set of inner codes is the Wozencraft ensemble
. The set of inner codes is the Wozencraft ensemble 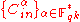 .
.Property of Justesen Code
As the linear codes in the Wonzencraft ensemble have the rate , Justesen code is the concatenated code
, Justesen code is the concatenated code 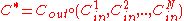 with the rate
with the rate  . We have the following theorem that estimates the distance of the concatenated code
. We have the following theorem that estimates the distance of the concatenated code 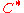 .
.Theorem
Let > 0.
> 0. 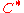 has relative distance at least
has relative distance at least  .
.Proof:
The idea of proving that the code
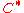 has the distance at least
has the distance at least 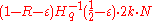 is to prove that the Hamming distance of two different codewords is at least
is to prove that the Hamming distance of two different codewords is at least 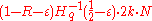 .
.Denote
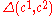 be the Hamming distance of two codewords
be the Hamming distance of two codewords 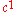 and
and 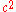 .
.So for any given
 and
and 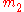 in
in 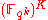 (
( ), we want to lower bound
), we want to lower bound 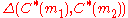 .
.Notice that if
 , then
, then  . So to the lower bound
. So to the lower bound 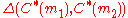 , we need to take into account the distance of
, we need to take into account the distance of 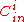 for i = 1,2,…,N.
for i = 1,2,…,N.Suppose
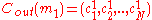 and
and 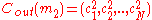 .
.Recall that
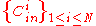 is a Wozencraft ensemble. Due to "Wonzencraft ensemble theorem", there are at least
is a Wozencraft ensemble. Due to "Wonzencraft ensemble theorem", there are at least 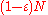 linear codes
linear codes 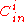 that have distance
that have distance 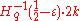 .
.So if for some
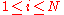 ,
, 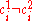 and
and 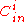 code has distance
code has distance 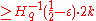 , then
, then 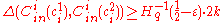 .
.Further, if we have
 numbers
numbers  such that
such that  and
and  code has distance
code has distance 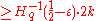 , then
, then  .
.So now the final task is to lower bound
 .
.Denote S be the set of all
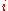 (
(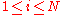 ) such that
) such that 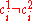 . Then
. Then  is the number of linear codes
is the number of linear codes 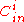 (
(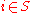 ) having the distance
) having the distance 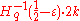 .
.Now we want to estimate
 . Obviously
. Obviously 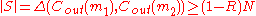 .
.Due to the Wozencraft Ensemble Theorem, there are at most
 linear codes having distance less than
linear codes having distance less than 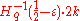 , so
, so 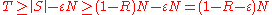 .
.Finally,we have
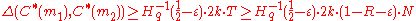 .
.This is true for any arbitrary
 . So
. So 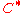 has the relative distance at least
has the relative distance at least  , which completes the proof.
, which completes the proof.Comments
We want to consider the "strongly explicit code". So the question is what the "strongly explicit code" is. Loosely speaking, for linear code, the "explicit" property is related to the complexity of constructing its generator matrix G. That means, we can compute the matrix in logarithmic space without using the brute force algorithm to verify that a code has a given satisfied distance.For the other codes that are not linear, we can consider the complexity of the encoding algorithm.
So by far, we can see that the Wonzencraft ensemble and Reed-Solomon codes are strongly explicit. Therefore we have the following result:
Corollary: The concatenated code
 is an asymptotically good code(that is, rate
is an asymptotically good code(that is, rate  > 0 and relative distance
> 0 and relative distance  > 0 for small q) and has a strongly explicit construction.
> 0 for small q) and has a strongly explicit construction.An example of a Justesen code
The following slightly different code is referred to as the Justesen code in MacWilliams/MacWilliams. It is the particular case of the above-consideredJustesen code for a very particular Wonzencraft ensemble:
Let R be a Reed-Solomon code of length N = 2m − 1, rank
Dimension (vector space)
In mathematics, the dimension of a vector space V is the cardinality of a basis of V. It is sometimes called Hamel dimension or algebraic dimension to distinguish it from other types of dimension...
K and minimum weight N − K + 1. The symbols of R are elements of F = GF(2m) and the codewords are obtained by taking every polynomial ƒ over F of degree less than K and listing the values of ƒ on the non-zero elements of F in some predetermined order. Let α be a primitive element of F. For a codeword a = (a1, ..., aN) from R, let b be the vector of length 2N over F given by
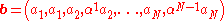
and let c be the vector of length 2N m obtained from b by expressing each element of F as a binary vector of length m. The Justesen code is the linear code containing all such c.
The parameters of this code are length 2m N, dimension m K and minimum distance
Minimum distance
The term minimum distance is used in several ways:* In geometry, the minimum distance of a collection of points P in a space is the smallest distance between any two points of the space....
at least

where
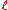 is the greatest integer satisfying
is the greatest integer satisfying  . (See MacWilliams/MacWilliams for a proof.)
. (See MacWilliams/MacWilliams for a proof.)See Also
- Wozencraft ensemble
- Concatenated error correction code
- Reed-Solomon error correctionReed–Solomon error correctionIn coding theory, Reed–Solomon codes are non-binary cyclic error-correcting codes invented by Irving S. Reed and Gustave Solomon. They described a systematic way of building codes that could detect and correct multiple random symbol errors...
- Linear CodeLinear codeIn coding theory, a linear code is an error-correcting code for which any linear combination of codewords is also a codeword. Linear codes are traditionally partitioned into block codes and convolutional codes, although Turbo codes can be seen as a hybrid of these two types. Linear codes allow for...

