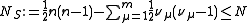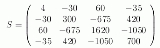
Jacobi eigenvalue algorithm
Encyclopedia
In numerical linear algebra
, the Jacobi eigenvalue algorithm is an iterative method
for the calculation of the eigenvalues and eigenvectors of a real
symmetric matrix. It is named after Carl Gustav Jacob Jacobi, who first proposed the method in 1846, but only became widely used in the 1950s with the advent of computers.
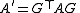
is symmetric and similar to A.
Furthermore, A′ has entries:
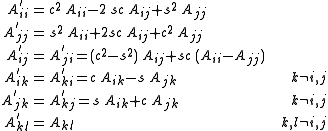
where s = sin(θ) and c = cos(θ).
Since G is orthogonal, A and A′ have the same Frobenius norm ||·||F (the square-root sum of squares of all components), however we can choose θ such that A′ij = 0, in which case A′ has a larger sum of squares on the diagonal:
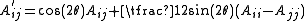
Set this equal to 0, and rearrange:
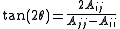
if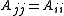
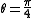
In order to optimize this effect, Aij should be the largest off-diagonal component, called the pivot.
The Jacobi eigenvalue method repeatedly performs rotations until the matrix becomes almost diagonal. Then the elements in the diagonal are approximations of the (real) eigenvalues of A.
is a pivot element, then by definition 
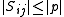for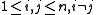 
. Since S has exactly 2 N := n ( n - 1) off-diag elements, we have 
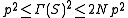or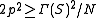 
. This implies
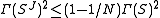or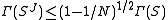 
,
i.e. the sequence of Jacobi rotations converges at least linearly by a factor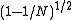
to a diagonal matrix.
A number of N Jacobi rotations is called a sweep; let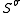
denote the result. The previous estimate yields
i.e. the sequence of sweeps converges at least linearly with a factor ≈
.
However the following result of Schönhage yields locally quadratic convergence. To this end let S have m distinct eigenvalues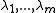
with multiplicities 
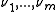and let d > 0 be the smallest distance of two different eigenvalues. Let us call a number of
Jacobi rotations a Schönhage-sweep. If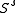
denotes the result then
Thus convergence becomes quadratic as soon as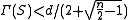
.
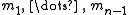with the property that 
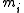is the index of the largest element in row i, (i = 1, …, n − 1) of the current S. Then (k, l) must be one of the pairs 
. Since only columns k and l change, only 
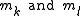must be updated, which again can be done in n steps. Thus each rotation has O(n) cost and one sweep has O(n3) cost which is equivalent to one matrix multiplication. Additionally the 
must be initialized before the process starts, this can be done in n2 steps.
Typically the Jacobi method converges within numerical precision after a small number of sweeps. Note that multiple eigenvalues reduce the number of iterations since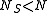
.
It calculates a vector e which contains the eigenvalues and a matrix E which contains the corresponding eigenvectors, i.e.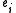
is an eigenvalue and the column 
an orthonormal eigenvector for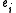 
, i = 1, …, n.
procedure jacobi(S ∈ Rn×n; out e ∈ Rn; out E ∈ Rn×n)
var
i, k, l, m, state ∈ N
s, c, t, p, y ∈ R
ind ∈ Nn
changed ∈ Ln
function maxind(k ∈ N) ∈ N ! index of largest off-diagonal element in row k
m := k+1
for i := k+2 to n do
if │Ski│ > │Skm│ then m := i endif
endfor
return m
endfunc
procedure update(k ∈ N; t ∈ R) ! update ek and its status
y := ek; ek := y+t
if changedk and (y=ek) then changedk := false; state := state−1
elsif (not changedk) and (y≠ek) then changedk := true; state := state+1
endif
endproc
procedure rotate(k,l,i,j ∈ N) ! perform rotation of Sij, Skl
┌ ┐ ┌ ┐┌ ┐
│Skl│ │c −s││Skl│
│ │ := │ ││ │
│Sij│ │s c││Sij│
└ ┘ └ ┘└ ┘
endproc
! init e, E, and arrays ind, changed
E := I; state := n
for k := 1 to n do indk := maxind(k); ek := Skk; changedk := true endfor
while state≠0 do ! next rotation
m := 1 ! find index (k,l) of pivot p
for k := 2 to n−1 do
if │Sk indk│ > │Sm indm│ then m := k endif
endfor
k := m; l := indm; p := Skl
! calculate c = cos φ, s = sin φ
y := (el−ek)/2; t := │y│+√(p2+y2)
s := √(p2+t2); c := t/s; s := p/s; t := p2/t
if y<0 then s := −s; t := −t endif
Skl := 0.0; update(k,−t); update(l,t)
! rotate rows and columns k and l
for i := 1 to k−1 do rotate(i,k,i,l) endfor
for i := k+1 to l−1 do rotate(k,i,i,l) endfor
for i := l+1 to n do rotate(k,i,l,i) endfor
! rotate eigenvectors
for i := 1 to n do
┌ ┐ ┌ ┐┌ ┐
│Eki│ │c −s││Eki│
│ │ := │ ││ │
│Eli│ │s c││Eli│
└ ┘ └ ┘└ ┘
endfor
! rows k, l have changed, update rows indk, indl
indk := maxind(k); indl := maxind(l)
loop
endproc
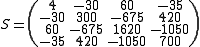
Then jacobi produces the following eigenvalues and eigenvectors after 3 sweeps (19 iterations) :
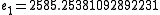
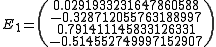
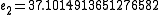
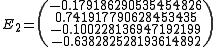
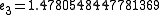
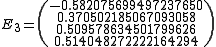
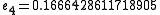
these link can explain the example
http://www.scribd.com/doc/24953275/Jacobi-Transformation-Used-for-Eigenproblems-for-Symmetric-Matrix
values are easily calculated.
Singular values
2-norm and spectral radius
Condition number
Rank
Pseudo-inverse
Least squares solution
Matrix exponential
Linear differential equations
, general nonsymmetric real and complex matrices as well as block matrices.
Since singular values of a real matrix are the square roots of the eigenvalues of the symmetric matrix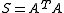
it can also be used for the calculation of these values. For this case, the method is modified in such a way that S must not be explicitly calculated which reduces the danger of round-off error
s. Note that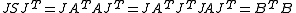
with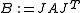 
.
The Jacobi Method is also well suited for parallelism.
Numerical linear algebra
Numerical linear algebra is the study of algorithms for performing linear algebra computations, most notably matrix operations, on computers. It is often a fundamental part of engineering and computational science problems, such as image and signal processing, Telecommunication, computational...
, the Jacobi eigenvalue algorithm is an iterative method
Iterative method
In computational mathematics, an iterative method is a mathematical procedure that generates a sequence of improving approximate solutions for a class of problems. A specific implementation of an iterative method, including the termination criteria, is an algorithm of the iterative method...
for the calculation of the eigenvalues and eigenvectors of a real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
symmetric matrix. It is named after Carl Gustav Jacob Jacobi, who first proposed the method in 1846, but only became widely used in the 1950s with the advent of computers.
Description
Let A be a symmetric matrix, and G = G(i,j,θ) be a Givens rotation matrix. Then: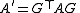is symmetric and similar to A.
Furthermore, A′ has entries:
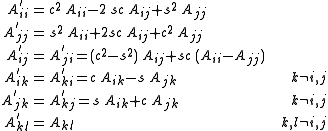
where s = sin(θ) and c = cos(θ).
Since G is orthogonal, A and A′ have the same Frobenius norm ||·||F (the square-root sum of squares of all components), however we can choose θ such that A′ij = 0, in which case A′ has a larger sum of squares on the diagonal:
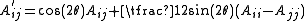
Set this equal to 0, and rearrange:
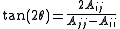
if
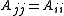
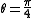
In order to optimize this effect, Aij should be the largest off-diagonal component, called the pivot.
The Jacobi eigenvalue method repeatedly performs rotations until the matrix becomes almost diagonal. Then the elements in the diagonal are approximations of the (real) eigenvalues of A.
Convergence
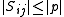If is a pivot element, then by definition for 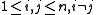. Since S has exactly 2 N := n ( n - 1) off-diag elements, we have 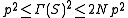or 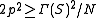. This implies 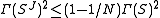or 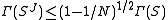,i.e. the sequence of Jacobi rotations converges at least linearly by a factor
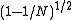to a diagonal matrix.A number of N Jacobi rotations is called a sweep; let
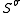denote the result. The previous estimate yields
-
,
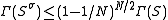i.e. the sequence of sweeps converges at least linearly with a factor ≈
.However the following result of Schönhage yields locally quadratic convergence. To this end let S have m distinct eigenvalues
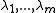with multiplicities 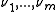and let d > 0 be the smallest distance of two different eigenvalues. Let us call a number of
Jacobi rotations a Schönhage-sweep. If
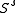denotes the result then
-
.
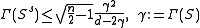Thus convergence becomes quadratic as soon as
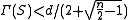.Cost
Each Jacobi rotation can be done in n steps when the pivot element p is known. However the search for p requires inspection of all N ≈ ½ n2 off-diag elements. We can reduce this to n steps too if we introduce an additional index array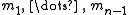 with the property that 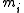is the index of the largest element in row i, (i = 1, …, n − 1) of the current S. Then (k, l) must be one of the pairs . 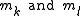Since only columns k and l change, only must be updated, which again can be done in n steps. Thus each rotation has O(n) cost and one sweep has O(n3) cost which is equivalent to one matrix multiplication. Additionally the must be initialized before the process starts, this can be done in n2 steps.Typically the Jacobi method converges within numerical precision after a small number of sweeps. Note that multiple eigenvalues reduce the number of iterations since
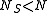.Algorithm
The following algorithm is a description of the Jacobi method in math-like notation.It calculates a vector e which contains the eigenvalues and a matrix E which contains the corresponding eigenvectors, i.e.
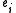is an eigenvalue and the column an orthonormal eigenvector for 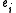, i = 1, …, n.procedure jacobi(S ∈ Rn×n; out e ∈ Rn; out E ∈ Rn×n)
var
i, k, l, m, state ∈ N
s, c, t, p, y ∈ R
ind ∈ Nn
changed ∈ Ln
function maxind(k ∈ N) ∈ N ! index of largest off-diagonal element in row k
m := k+1
for i := k+2 to n do
if │Ski│ > │Skm│ then m := i endif
endfor
return m
endfunc
procedure update(k ∈ N; t ∈ R) ! update ek and its status
y := ek; ek := y+t
if changedk and (y=ek) then changedk := false; state := state−1
elsif (not changedk) and (y≠ek) then changedk := true; state := state+1
endif
endproc
procedure rotate(k,l,i,j ∈ N) ! perform rotation of Sij, Skl
┌ ┐ ┌ ┐┌ ┐
│Skl│ │c −s││Skl│
│ │ := │ ││ │
│Sij│ │s c││Sij│
└ ┘ └ ┘└ ┘
endproc
! init e, E, and arrays ind, changed
E := I; state := n
for k := 1 to n do indk := maxind(k); ek := Skk; changedk := true endfor
while state≠0 do ! next rotation
m := 1 ! find index (k,l) of pivot p
for k := 2 to n−1 do
if │Sk indk│ > │Sm indm│ then m := k endif
endfor
k := m; l := indm; p := Skl
! calculate c = cos φ, s = sin φ
y := (el−ek)/2; t := │y│+√(p2+y2)
s := √(p2+t2); c := t/s; s := p/s; t := p2/t
if y<0 then s := −s; t := −t endif
Skl := 0.0; update(k,−t); update(l,t)
! rotate rows and columns k and l
for i := 1 to k−1 do rotate(i,k,i,l) endfor
for i := k+1 to l−1 do rotate(k,i,i,l) endfor
for i := l+1 to n do rotate(k,i,l,i) endfor
! rotate eigenvectors
for i := 1 to n do
┌ ┐ ┌ ┐┌ ┐
│Eki│ │c −s││Eki│
│ │ := │ ││ │
│Eli│ │s c││Eli│
└ ┘ └ ┘└ ┘
endfor
! rows k, l have changed, update rows indk, indl
indk := maxind(k); indl := maxind(l)
loop
endproc
Example
Let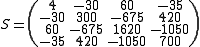Then jacobi produces the following eigenvalues and eigenvectors after 3 sweeps (19 iterations) :
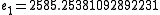
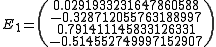
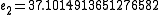
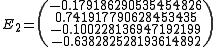
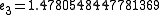
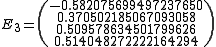
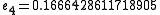
these link can explain the example
http://www.scribd.com/doc/24953275/Jacobi-Transformation-Used-for-Eigenproblems-for-Symmetric-Matrix
Applications for real symmetric matrices
When the eigenvalues (and eigenvectors) of a symmetric matrix are known, the followingvalues are easily calculated.
Singular values
- The singular values of a (square) matrix A are the square roots of the (non-negative) eigenvalues of
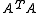. In case of a symmetric matrix S we have of 
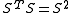, hence the singular values of S are the absolute values of the eigenvalues of S
2-norm and spectral radius
- The 2-norm of a matrix A is the norm based on the Euclidean vectornorm, i.e. the largest value
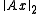when x runs through all vectors with 
. It is the largest singular value of A. In case of a symmetric matrix it is largest absolute value of its eigenvectors and thus equal to its spectral radius.
Condition number
- The condition number of a nonsingular matrix A is defined as
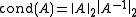. In case of a symmetric matrix it is the absolute value of the quotient of the largest and smallest eigenvalue. Matrices with large condition numbers can cause numerically unstable results: small perturbation can result in large errors. Hilbert matrices are the most famous ill-conditioned matrices. For example, the fourth-order Hilbert matrix has a condition of 15514, while for order 8 it is 2.7 × 108.
Rank
- A matrix A has rank r if it has r columns that are linearly independent while the remaining columns are linearly dependent on these. Equivalently, r is the dimension of the range of A. Furthermore it is the number of nonzero singular values.
- In case of a symmetric matrix r is the number of nonzero eigenvalues. Unfortunately because of rounding errors numerical approximations of zero eigenvalues may not be zero (it may also happen that a numerical approximation is zero while the true value is not). Thus one can only calculate the numerical rank by making a decision which of the eigenvalues are close enough to zero.
Pseudo-inverse
- The pseudo inverse of a matrix A is the unique matrix
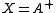for which AX and XA are symmetric and for which AXA = A, XAX = X holds. If A is nonsingular, then '
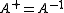. - When procedure jacobi (S, e, E) is called, then the relation
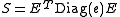holds where Diag(e) denotes the diagonal matrix with vector e on the diagonal. Let 
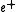denote the vector where 
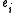is replaced by 
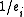if 
and by 0 if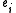 
is (numerically close to) zero. Since matrix E is orthogonal, it follows that the pseudo-inverse of S is given by 
.
Least squares solution
- If matrix A does not have full rank, there may not be a solution of the linear system Ax = b. However one can look for a vector x for which
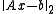is minimal. The solution is 
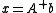. In case of a symmetric matrix S as before, one has 
.
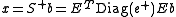Matrix exponential
- From
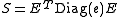one finds 
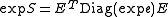where exp e is the vector where 
is replaced by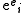 
. In the same way, f(S) can be calculated in an obvious way for any (analytic) function f.
Linear differential equations
- The differential equation x' = Ax, x(0) = a has the solution x(t) = exp(t A) a. For a symmetric matrix S, it follows that
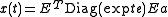. If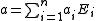 
is the expansion of a by the eigenvectors of S, then 
. - Let
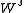be the vector space spanned by the eigenvectors of S which correspond to a negative eigenvalue and 
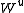analogously for the positive eigenvalues. If 
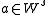then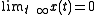 
i.e. the equilibrium point 0 is attractive to x(t). If 
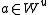then 
, i.e. 0 is repulsive to x(t). 
and 
are called stable and unstable manifolds for S. If a has components in both manifolds, then one component is attracted and one component is repelled. Hence x(t) approache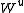s 
as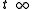 
.
Generalizations
The Jacobi Method has been generalized to complex Hermitian matricesJacobi method for complex Hermitian matrices
In mathematics, the Jacobi method for complex Hermitian matrices is a generalization of the Jacobi iteration method. The Jacobi iteration method is also explained in "Introduction to Linear Algebra" by .- Derivation :...
, general nonsymmetric real and complex matrices as well as block matrices.
Since singular values of a real matrix are the square roots of the eigenvalues of the symmetric matrix
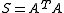it can also be used for the calculation of these values. For this case, the method is modified in such a way that S must not be explicitly calculated which reduces the danger of round-off errorRound-off error
A round-off error, also called rounding error, is the difference between the calculated approximation of a number and its exact mathematical value. Numerical analysis specifically tries to estimate this error when using approximation equations and/or algorithms, especially when using finitely many...
s. Note that
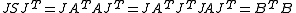with 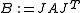.The Jacobi Method is also well suited for parallelism.