
Inventor's paradox
Encyclopedia
The inventor's paradox is a phenomenon that occurs in seeking a solution to a given problem. Instead of solving a specific type of problem, which would seem intuitively easier, it is easier to solve a more general problem, which covers the specifics of the sought after solution. It has been used to describe phenomena in mathematics, programming, and logic, as well as other areas that involve critical thinking.
, George Pólya
introduces what he defines as the inventor's paradox:
or, in other words, to solve what you desire, you may have to solve more than what you actually want to in order to get a properly working flow of information.
When solving a problem, the natural inclination typically is to remove as much excessive variability and produce limitations on the subject at hand. Doing this can create unforeseen and intrinsically awkward parameters. The goal is to find elegant and relatively simple solutions to broader problems, allowing for the ability to focus on the specific portion you were initially concerned with.
There lies the inventor's paradox, that it is often significantly easier to find a general solution than a more specific one, which may naturally have a simpler algorithm and cleaner design, and typically can take less time to solve in comparison with a particular problem.

This process, although not impossible to do in your head, can prove to be difficult for most. However, if the ability to generalize the problem exists, in this case by reducing the sequence to:
In this form, the example can be solved by most without the use of a calculator.
Although appearing in several applications, it can be easiest to explain through inspection a relatively simple mathematical sequence.

and further along in the sequence:
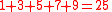
In allowing the sequence to expand to a point where the sum cannot be found quickly, we can simplify by finding that the sum of consecutive odd numbers follows:
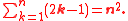
, the internet and Apache
web servers plug-ins are primary examples of such practice. In the investigation of the semantics of language, many logicians find themselves facing this paradox. An example of application being how they are inherently concerned with the conditions of truth within a sentence, and not, in fact, concerned with the conditions under which a sentence can be truly asserted.
Additionally, the paradox has been shown to have applications in industry.
History
In the book How to Solve ItHow to Solve It
How to Solve It is a small volume by mathematician George Pólya describing methods of problem solving.- Four principles :How to Solve It suggests the following steps when solving a mathematical problem:...
, George Pólya
George Pólya
George Pólya was a Hungarian mathematician. He was a professor of mathematics from 1914 to 1940 at ETH Zürich and from 1940 to 1953 at Stanford University. He made fundamental contributions to combinatorics, number theory, numerical analysis and probability theory...
introduces what he defines as the inventor's paradox:
or, in other words, to solve what you desire, you may have to solve more than what you actually want to in order to get a properly working flow of information.
When solving a problem, the natural inclination typically is to remove as much excessive variability and produce limitations on the subject at hand. Doing this can create unforeseen and intrinsically awkward parameters. The goal is to find elegant and relatively simple solutions to broader problems, allowing for the ability to focus on the specific portion you were initially concerned with.
There lies the inventor's paradox, that it is often significantly easier to find a general solution than a more specific one, which may naturally have a simpler algorithm and cleaner design, and typically can take less time to solve in comparison with a particular problem.
Mathematics
The sum of numbers sequentially from 1-99:
This process, although not impossible to do in your head, can prove to be difficult for most. However, if the ability to generalize the problem exists, in this case by reducing the sequence to:

In this form, the example can be solved by most without the use of a calculator.
Although appearing in several applications, it can be easiest to explain through inspection a relatively simple mathematical sequence.


and further along in the sequence:
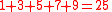
In allowing the sequence to expand to a point where the sum cannot be found quickly, we can simplify by finding that the sum of consecutive odd numbers follows:
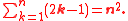
Programming
As an example in applying the same logic, it may be harder to solve a 25-case problem than it would be to solve an n-case problem, and then applying it to the case where n=25.Applications
This paradox has applications in writing efficient programs. It is intuitive to write programs that are specialized, but in practice it can become easier to develop more generalized procedures. According to Bruce Tate, some of the most successful frameworks are simple generalizations of complex problems, and he says that Visual BasicVisual Basic
Visual Basic is the third-generation event-driven programming language and integrated development environment from Microsoft for its COM programming model...
, the internet and Apache
Apache
Apache is the collective term for several culturally related groups of Native Americans in the United States originally from the Southwest United States. These indigenous peoples of North America speak a Southern Athabaskan language, which is related linguistically to the languages of Athabaskan...
web servers plug-ins are primary examples of such practice. In the investigation of the semantics of language, many logicians find themselves facing this paradox. An example of application being how they are inherently concerned with the conditions of truth within a sentence, and not, in fact, concerned with the conditions under which a sentence can be truly asserted.
Additionally, the paradox has been shown to have applications in industry.

