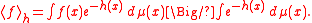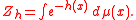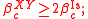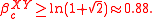Griffiths inequality
Encyclopedia
In statistical mechanics
, the Griffiths inequality (sometimes also called Griffiths–Kelly–Sherman inequality or GKS inequality), named after Robert B. Griffiths, is a correlation inequality
for ferromagnetic spin systems. Informally, it says that in ferromagnetic spin systems, if the 'a-priori distribution' of the spin is invariant under spin flipping, the correlation of any monomial of the spins is non-negative; and the two point correlation of two monomial of the spins is non-negative.
The inequality was proved by Griffiths for Ising ferromagnets with two-body interactions, then generalised by Kelly and Sherman to interactions involving an arbitrary number of spins, and then by Griffiths to systems with arbitrary spins. A more general formulation was given by Ginibre
, and is now called the Ginibre inequality.
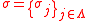be a configuration of (continuous or discrete) spins on a lattice
Λ. If A ⊂ Λ is a list of lattice sites, possibly with duplicates, let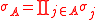
be the product of the spins in A.
Assign an a-priori measure dμ(σ) on the spins;
let H be an energy functional of the form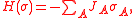
where the sum is over lists of sites A, and let
be the partition function
. As usual,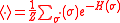
stands for the ensemble average
.
The system is called ferromagnetic if, for any list of sites A, JA ≥ 0. The system is called invariant under spin flipping if, for any j in Λ, the measure μ is preserved under the sign flipping map σ → τ, where
for any list of spins A.
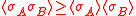
for any lists of spins A and B.
The first inequality is a special case of the second one, corresponding to B = ∅.
Proof of first inequality: Expand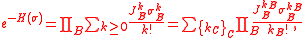
then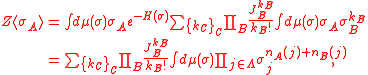
where nA(j) stands for the number of times that j appears in A. Now, by invariance under spin flipping,
if at least one n(j) is odd, and the same expression is obviously non-negative for even values of n. Therefore Z<σA>≥0, hence also <σA>≥0.
Proof of second inequality. For the second Griffiths inequality, double the random variable, i.e. consider a second copy of the spin,
, with the same distribution of 
. Then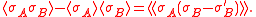
Introduce the new variables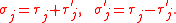
The doubled system
is ferromagnetic in 
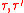because 
is a polynomial in 
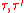with positive coefficients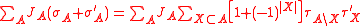
Besides the measure on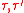
is invariant under spin flipping because 
is.
Finally the monomials
, 
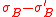are polynomials in 
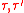with positive coefficients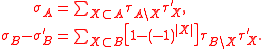
The first Griffiths inequality applied to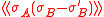
gives the result.
More details are in.
. For functions f, h on Γ, denote
Let A be a set of real functions on Γ such that. for every f1,f2,...,fn in A, and for any choice of signs ±,
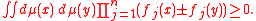
Then, for any f,g,-h in the convex cone
generated by A,
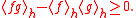
Then
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
, the Griffiths inequality (sometimes also called Griffiths–Kelly–Sherman inequality or GKS inequality), named after Robert B. Griffiths, is a correlation inequality
Correlation inequality
In probability and statistics, a correlation inequality is one of a number of inequalities satisfied by the correlation functions of a model. Such inequalities are of particular use in statistical mechanics and in percolation theory.Examples include:...
for ferromagnetic spin systems. Informally, it says that in ferromagnetic spin systems, if the 'a-priori distribution' of the spin is invariant under spin flipping, the correlation of any monomial of the spins is non-negative; and the two point correlation of two monomial of the spins is non-negative.
The inequality was proved by Griffiths for Ising ferromagnets with two-body interactions, then generalised by Kelly and Sherman to interactions involving an arbitrary number of spins, and then by Griffiths to systems with arbitrary spins. A more general formulation was given by Ginibre
Jean Ginibre
Jean Ginibre is a French mathematical physicist, known in particular for his contributions to random matrix theory , statistical mechanics , and partial differential equations. He received the Paul Langevin Prize in 1969.Jean Ginibre is Emeritus Professor at Paris-Sud 11 University....
, and is now called the Ginibre inequality.
Definitions
Let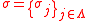 be a configuration of (continuous or discrete) spins on a latticeLattice (group)
In mathematics, especially in geometry and group theory, a lattice in Rn is a discrete subgroup of Rn which spans the real vector space Rn. Every lattice in Rn can be generated from a basis for the vector space by forming all linear combinations with integer coefficients...
Λ. If A ⊂ Λ is a list of lattice sites, possibly with duplicates, let
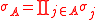be the product of the spins in A.Assign an a-priori measure dμ(σ) on the spins;
let H be an energy functional of the form
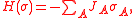
where the sum is over lists of sites A, and let
be the partition function
Partition function (statistical mechanics)
Partition functions describe the statistical properties of a system in thermodynamic equilibrium. It is a function of temperature and other parameters, such as the volume enclosing a gas...
. As usual,
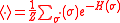
stands for the ensemble average
Ensemble average
In statistical mechanics, the ensemble average is defined as the mean of a quantity that is a function of the micro-state of a system , according to the distribution of the system on its micro-states in this ensemble....
.
The system is called ferromagnetic if, for any list of sites A, JA ≥ 0. The system is called invariant under spin flipping if, for any j in Λ, the measure μ is preserved under the sign flipping map σ → τ, where
First Griffiths inequality
In a ferromagnetic spin system which is invariant under spin flipping,for any list of spins A.
Second Griffiths inequality
In a ferromagnetic spin system which is invariant under spin flipping,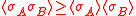for any lists of spins A and B.
The first inequality is a special case of the second one, corresponding to B = ∅.
Proof
Observe that the partition function is non-negative by definition.Proof of first inequality: Expand
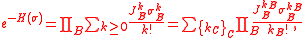
then
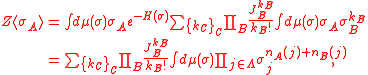
where nA(j) stands for the number of times that j appears in A. Now, by invariance under spin flipping,
if at least one n(j) is odd, and the same expression is obviously non-negative for even values of n. Therefore Z<σA>≥0, hence also <σA>≥0.
Proof of second inequality. For the second Griffiths inequality, double the random variable, i.e. consider a second copy of the spin,
, with the same distribution of . Then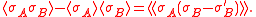Introduce the new variables
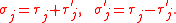
The doubled system
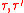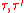is ferromagnetic in because is a polynomial in with positive coefficients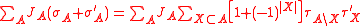Besides the measure on
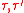is invariant under spin flipping because is.Finally the monomials
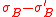, are polynomials in 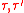with positive coefficients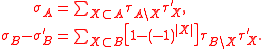The first Griffiths inequality applied to
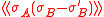gives the result.More details are in.
Extension: Ginibre inequality
The Ginibre inequality is an extension, found by Jean Ginibre, of the Griffiths inequality.Formulation
Let (Γ, μ) be a probability spaceProbability space
In probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
. For functions f, h on Γ, denote
Let A be a set of real functions on Γ such that. for every f1,f2,...,fn in A, and for any choice of signs ±,
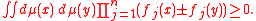
Then, for any f,g,-h in the convex cone
Convex cone
In linear algebra, a convex cone is a subset of a vector space over an ordered field that is closed under linear combinations with positive coefficients.-Definition:...
generated by A,
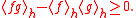
Proof
Let
Then
-
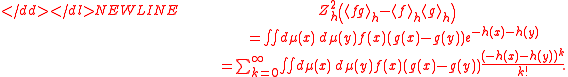
Now the inequality follows from the assumption and from the identity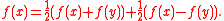
Examples
- To recover the (second) Griffiths inequality, take Γ = {-1, +1}Λ, where Λ is a lattice, and let μ be a measure on Γ that is invariant under sign flipping. The cone A of polynomials with positive coefficients satisfies the assumptions of the Ginibre inequality.
- (Γ, μ) is a commutative compact groupCompact groupIn mathematics, a compact group is a topological group whose topology is compact. Compact groups are a natural generalisation of finite groups with the discrete topology and have properties that carry over in significant fashion...
with the Haar measureHaar measureIn mathematical analysis, the Haar measure is a way to assign an "invariant volume" to subsets of locally compact topological groups and subsequently define an integral for functions on those groups....
, A is the cone of real positive definite functions on Γ. - Γ is a totally ordered set, A is the cone of real positive non-decreasing functions on Γ. This yields Chebyshev's sum inequalityChebyshev's sum inequalityIn mathematics, Chebyshev's sum inequality, named after Pafnuty Chebyshev, states that ifa_1 \geq a_2 \geq \cdots \geq a_nandb_1 \geq b_2 \geq \cdots \geq b_n,then...
. For extension to partially ordered sets, see FKG inequalityFKG inequalityThe FKG inequality is a correlation inequality, a fundamental tool in statistical mechanics and probabilistic combinatorics , due to...
.
Applications
- The thermodynamic limitThermodynamic limitIn thermodynamics, particularly statistical mechanics, the thermodynamic limit is reached as the number of particles in a system, N, approaches infinity...
of the correlations of the ferromagnetic Ising model (with non-negative external field h and free boundary conditions) exists.
- This is because increasing the volume is the same as switching on new couplings JB for a certain subset B. By the second Griffiths inequality
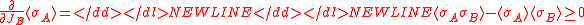
- Hence
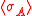is monotonically increasing with the volume; then it converges since it is bounded by 1.
- The one-dimensional, ferromagnetic Ising model with interactions
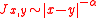displays a phase transition if 
.
- This property can be showed in a hierachical approximation, that differs from the full model by the absence of some interactions: arguing as above with the second Griffiths inequality, the results carries over the full model.
- Ginibre applied the Ginibre inequality to prov the existence of the thermodynamic limit for the free energyThermodynamic free energyThe thermodynamic free energy is the amount of work that a thermodynamic system can perform. The concept is useful in the thermodynamics of chemical or thermal processes in engineering and science. The free energy is the internal energy of a system less the amount of energy that cannot be used to...
and spin correlations for the classical XY model.
- Aizenman and Simon used the Ginibre inequality to prove that the two point spin correlation of the ferromagnetic classical XY model in dimension
, coupling 
and inverse temperature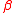 
is dominated by (i.e. has upper bound given by) the two point correlation of the ferromagnetic Ising modelIsing modelThe Ising model is a mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables called spins that can be in one of two states . The spins are arranged in a graph , and each spin interacts with its nearest neighbors...
in dimension
, coupling 
, and inverse temperature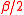 
-
- Hence the critical
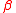of the XY model cannot be smaller than the double of the critical temperature of the Ising model
- in dimension D = 2 and coupling J = 1, this gives
- There exists a version of the Ginibre inequality for the Coulomb gas that implies the existence of thermodynamic limit of correlations.
- Other applications (phase transitions in spin systems, XY model, XYZ quantum chain) are reviewed in.
- Hence the critical
- Hence
