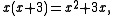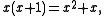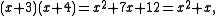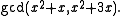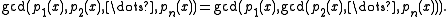Greatest common divisor of two polynomials
Encyclopedia
Informally, the greatest common divisor (GCD) of two polynomial
s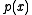
and 
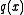is the largest polynomial that divides both 
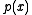and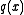 
evenly. The definition is modeled on the concept of the greatest common divisor
of two integer
s, the greatest integer that divides both. For polynomials, the situation is slightly more complicated, because there is no canonical
order
which we can use to say which polynomial is "biggest." Instead, the GCD is chosen so its degree
is as great as possible, and often so that its leading coefficient equals one (i.e., it is monic). The greatest common divisor is also sometimes referred to as the greatest common factor or the highest common factor.
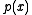and 
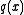be polynomials, not both zero, with coefficients in a field
.
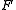A greatest common divisor of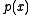
and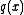 
is a polynomial 
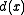of highest degree such that 
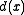is a divisor
of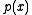
and of 
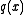. We may denote the greatest common divisor of 
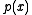and 
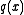by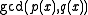 
.
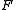may be, for example, the complex numbers, the real numbers or the rational numbers.
If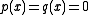
, then every polynomial is a common divisor of 
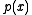and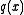 
. Thus no greatest common divisor exists in this case.
We require that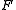
be a field and that 
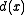be monic. Under these two hypotheses, the GCD exists and is uniquely defined.
They are necessary hypotheses. For example, suppose we allow F=Z/6Z, which is not a field. Then we have
and
after reduction modulo six (see modular arithmetic
). This shows that
and 
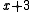would both satisfy the definition of
Suppose, on the other hand, that we did not require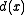
to be monic. In that case, whenever 
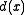satisfied the definition of 
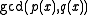, so would k•d(x) for any nonzero scalar k in F. Again, the GCD would not be uniquely determined.
The constant 1 is always a common divisor of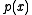
and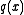 
; we may regard it as a monic polynomial of degree zero. If 
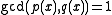, we say 
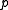and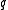 
are relatively prime.
Example one: Find the GCD of x2 + 7x + 6 and x2 − 5x − 6.
x2 + 7x + 6 = (x + 1)(x + 6)
x2 − 5x − 6 = (x + 1)(x − 6)
Thus, their GCD is x + 1.
is a fast method which works for any pair of polynomials. It makes repeated use of polynomial long division
or synthetic division
. When using this algorithm on two numbers, the size of the numbers decreases at each stage. With polynomials, the degree of the polynomials decreases at each stage. The last nonzero remainder, made monic if necessary, is the GCD of the two polynomials.
Example: Find the GCD of x2 + 7x + 6 and x2 − 5x − 6.
Since x + 1 is the last nonzero remainder, the GCD of these polynomials is x + 1.
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s
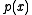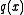and is the largest polynomial that divides both 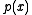and 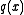evenly. The definition is modeled on the concept of the greatest common divisorGreatest common divisor
In mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to...
of two integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s, the greatest integer that divides both. For polynomials, the situation is slightly more complicated, because there is no canonical
Canonical
Canonical is an adjective derived from canon. Canon comes from the greek word κανών kanon, "rule" or "measuring stick" , and is used in various meanings....
order
Total order
In set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...
which we can use to say which polynomial is "biggest." Instead, the GCD is chosen so its degree
Degree of a polynomial
The degree of a polynomial represents the highest degree of a polynominal's terms , should the polynomial be expressed in canonical form . The degree of an individual term is the sum of the exponents acting on the term's variables...
is as great as possible, and often so that its leading coefficient equals one (i.e., it is monic). The greatest common divisor is also sometimes referred to as the greatest common factor or the highest common factor.
Formal definition
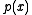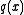Let and be polynomials, not both zero, with coefficients in a fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
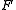.A greatest common divisor of
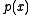and 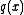is a polynomial 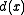of highest degree such that 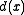is a divisorDivisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...
of
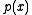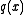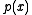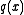and of . We may denote the greatest common divisor of and by .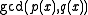
- Note: If
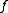is another polynomial, then it too is a greatest common divisor of 
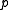and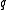 
if and only if 
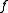is equal to 
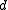multiplied by an element of 
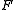. Such polynomials are effectively equivalent, and it is convenient to avoid having alternative equivalent greatest common divisors. For this reason it is usual to define the greatest common divisor of 
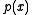and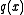 
as the unique monic polynomial which satisfies the above definition.
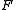may be, for example, the complex numbers, the real numbers or the rational numbers.If
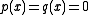, then every polynomial is a common divisor of 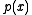and 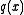. Thus no greatest common divisor exists in this case.We require that
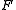be a field and that 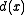be monic. Under these two hypotheses, the GCD exists and is uniquely defined.They are necessary hypotheses. For example, suppose we allow F=Z/6Z, which is not a field. Then we have
and
after reduction modulo six (see modular arithmetic
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
). This shows that
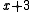and would both satisfy the definition of
Suppose, on the other hand, that we did not require
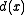to be monic. In that case, whenever 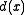satisfied the definition of 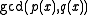, so would k•d(x) for any nonzero scalar k in F. Again, the GCD would not be uniquely determined.The constant 1 is always a common divisor of
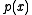and 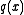; we may regard it as a monic polynomial of degree zero. If 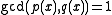, we say 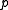and 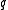are relatively prime.Properties
- As stated above, the GCD of two polynomials, not both zero, with coefficients from a field, exists and is unique.
- If
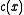is any common divisor of 
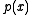and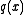 
, then 
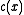divides 
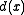. This is sometimes given in the definition instead of requiring 
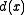to be the common divisor of highest degree. The two definitions are equivalent.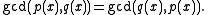 
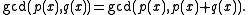
- For any nonzero scalar k in F,
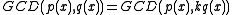. - Hence
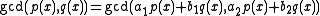for any scalars 
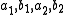such that 
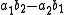is not equal to zero. - Likewise, if
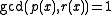, then 
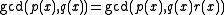. - The GCD of two polynomials,
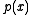and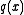 
, is the smallest-degree polynomial which can be written as a linear combination of 
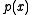and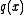 
. That is, there exist some polynomials, in the same field, 
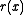and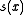 
, not necessarily unique, such that
-
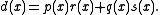
- It is possible to define the GCD of three or more polynomials inductively. Explicitly:
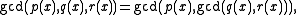
- and
Methods for finding the GCD
There are several ways to find the greatest common divisor of two polynomials. Two of them are:- FactorizationFactorizationIn mathematics, factorization or factoring is the decomposition of an object into a product of other objects, or factors, which when multiplied together give the original...
, in which one finds the factors of each expression, then selects the set of common factors held by all from within each set of factors. - The Euclidean algorithmEuclidean algorithmIn mathematics, the Euclidean algorithm is an efficient method for computing the greatest common divisor of two integers, also known as the greatest common factor or highest common factor...
, which can be used to find the GCD of two polynomials in the same manner as for two numbers.
Factoring
To find the GCD of two polynomials using factoring, simply factor the two polynomials completely. Then, take the product of all common factors. At this stage, we do not necessarily have a monic polynomial, so finally multiply this by a constant to make it a monic polynomial. This will be the GCD of the two polynomials as it includes all common divisors and is monic.Example one: Find the GCD of x2 + 7x + 6 and x2 − 5x − 6.
x2 + 7x + 6 = (x + 1)(x + 6)
x2 − 5x − 6 = (x + 1)(x − 6)
Thus, their GCD is x + 1.
Euclidean algorithm
Factoring polynomials can be difficult, especially if the polynomials have large degree. The Euclidean algorithmEuclidean algorithm
In mathematics, the Euclidean algorithm is an efficient method for computing the greatest common divisor of two integers, also known as the greatest common factor or highest common factor...
is a fast method which works for any pair of polynomials. It makes repeated use of polynomial long division
Polynomial long division
In algebra, polynomial long division is an algorithm for dividing a polynomial by another polynomial of the same or lower degree, a generalised version of the familiar arithmetic technique called long division...
or synthetic division
Synthetic division
Synthetic division is a method of performing polynomial long division, with less writing and fewer calculations. It is mostly taught for division by binomials of the formx - a,\ but the method generalizes to division by any monic polynomial...
. When using this algorithm on two numbers, the size of the numbers decreases at each stage. With polynomials, the degree of the polynomials decreases at each stage. The last nonzero remainder, made monic if necessary, is the GCD of the two polynomials.
Example: Find the GCD of x2 + 7x + 6 and x2 − 5x − 6.
- x2 + 7x + 6 = (x2 − 5x − 6)(1) + (x + 1)(12)
- x2 − 5x − 6 = (x + 1)(x − 6) + 0
Since x + 1 is the last nonzero remainder, the GCD of these polynomials is x + 1.