Golden section search
Encyclopedia
Golden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
. The algorithm is closely related to a Fibonacci search (also described below) and to a binary search. Golden section search was introduced by Kiefer
Jack Kiefer (mathematician)
Jack Carl Kiefer was an American statistician.- Biography :Jack Kiefer was born on January 25, 1924, in Cincinnati, Ohio, to Carl Jack Kiefer and Marguerite K. Rosenau...
(1953), and Fibonacci search by Avriel and Wilde (1966).
Basic idea
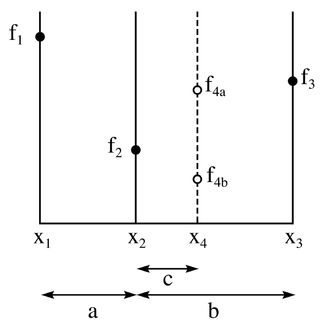
The diagram above illustrates a single step in the technique for finding a minimum. The functional values of
are on the vertical axis, and the horizontal axis is the x parameter. The value of 
has already been evaluated at the three points: 
, 
, and 
. Since 
is smaller than either 
or 
, it is clear that a minimum lies inside the interval from 
to 
(since f is unimodal).The next step in the minimization process is to "probe" the function by evaluating it at a new value of x, namely
. It is most efficient to choose 
somewhere inside the largest interval, i.e. between 
and 
. From the diagram, it is clear that if the function yields 
then a minimum lies between 
and 
and the new triplet of points will be 
, 
, and 
. However if the function yields the value 
then a minimum lies between 
and 
, and the new triplet of points will be 
, 
, and 
. Thus, in either case, we can construct a new narrower search interval that is guaranteed to contain the function's minimum.Probe point selection
From the diagram above, it is seen that the new search interval will be either between
and 
with a length of a+c , or between 
and 
with a length of b . The golden section search requires that these intervals be equal. If they are not, a run of "bad luck" could lead to the wider interval being used many times, thus slowing down the rate of convergence. To ensure that b = a+c, the algorithm should choose 
.However there still remains the question of where
should be placed in relation to 
and 
. The golden section search chooses the spacing between these points in such a way that these points have the same proportion of spacing as the subsequent triple 
or 
. By maintaining the same proportion of spacing throughout the algorithm, we avoid a situation in which 
is very close to 
or 
, and guarantee that the interval width shrinks by the same constant proportion in each step.Mathematically, to ensure that the spacing after evaluating
is proportional to the spacing prior to that evaluation, if 
is 
and our new triplet of points is 
, 
, and 
then we want:
However, if
is 
and our new triplet of points is 
, 
, and 
then we want:
Eliminating c from these two simultaneous equations yields:
or
where φ is the golden ratio
Golden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
:
The appearance of the golden ratio in the proportional spacing of the evaluation points is how this search algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
gets its name.
Termination condition
In addition to a routine for reducing the size of the bracketing of the solution, a complete algorithm must have a termination condition. The one provided in the book Numerical Recipes in C is based on testing the gaps among
, 
, 
and 
, terminating when within the relative accuracy bounds:
where
is a tolerance parameter of the algorithm and 
is the absolute valueAbsolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
of
. The check is based on the bracket size relative to its central value, because that relative error in 
is approximately proportional to the squared absolute error in 
in typical cases. For that same reason, the Numerical Recipes text recommends that 
where 
is the required absolute precision of 
.Recursive algorithm
double phi = (1 + Math.sqrt(5)) / 2;
double resphi = 2 - phi;
// a and c are the current bounds; the minimum is between them.
// b is a center point
// f(x) is some mathematical function elsewhere defined
// a corresponds to x1; b corresponds to x2; c corresponds to x3
// x corresponds to x4
public double goldenSectionSearch(double a, double b, double c, double tau) {
double x;
if (c - b > b - a)
x = b + resphi * (c - b);
else
x = b - resphi * (b - a);
if (Math.abs(c - a) < tau * (Math.abs(b) + Math.abs(c)))
return (c + a) / 2;
if (f(x) < f(b)) {
if (c - b > b - a) return goldenSectionSearch(b, x, c, tau);
else return goldenSectionSearch(a, x, b, tau);
}
else {
if (c - b > b - a) return goldenSectionSearch(a, b, x, tau);
else return goldenSectionSearch(x, b, c, tau);
}
}
To realise the advantage of golden section search, the function
would be implemented with caching, so that in all invocations of goldenSectionSearch(..) above, except the first, 
would have already been evaluated previously — the result of the calculation will be re-used, bypassing the (perhaps expensive) explicit evaluation of the function. Together with a slightly smaller number of recursions, this 50% saving in the number of calls to 
is the main algorithmic advantage over Ternary searchTernary search
A ternary search algorithm is a technique in computer science for finding the minimum or maximum of a unimodal function...
.
Fibonacci search
A very similar algorithm can also be used to find the extremum (minimum or maximum) of a sequenceSequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
of values that has a single local minimum or local maximum. In order to approximate the probe positions of golden section search while probing only integer sequence indices, the variant of the algorithm for this case typically maintains a bracketing of the solution in which the length of the bracketed interval is a Fibonacci number
Fibonacci number
In mathematics, the Fibonacci numbers are the numbers in the following integer sequence:0,\;1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89,\;144,\; \ldots\; ....
. For this reason, the sequence variant of golden section search is often called Fibonacci search
Fibonacci search technique
In computer science, the Fibonacci search technique is a method of searching a sorted array using a divide and conquer algorithm that narrows down possible locations with the aid of Fibonacci numbers.Compared to binary search, Fibonacci search examines...
.