
Froda's theorem
Encyclopedia
In mathematics
, Froda's theorem, named after Alexandru Froda
, describes the set of discontinuities of a (monotone) real-valued function
of a real variable. Usually, this theorem appears in literature without Froda's name being mentioned. However, this result was first proven by A. Froda in 1929.
It is obvious that if the function is continuous at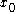 then the jump at
then the jump at 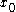 is zero. Moreover, if
is zero. Moreover, if 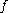 is not continuous in
is not continuous in 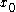 , the jump can be zero at
, the jump can be zero at 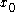 if
if 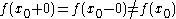 .
.
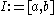 be an interval and
be an interval and 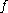 defined on
defined on 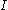 an increasing
an increasing
function. We have
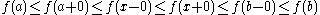
for any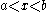 . Let
. Let 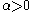 and let
and let 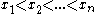 be
be  points inside
points inside 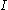 at which the jump of
at which the jump of 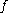 is greater or equal to
is greater or equal to  :
:

We have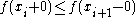 or
or 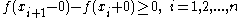 .
.
Then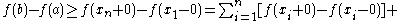
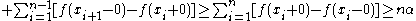
and hence: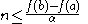 .
.
Since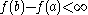 we have that the number of points at which the jump is greater than
we have that the number of points at which the jump is greater than  is finite or zero.
is finite or zero.
We define the following sets:
 ,
,
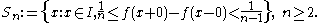
We have that each set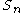 is finite or the empty set
is finite or the empty set
. The union
 contains all points at which the jump is positive and hence contains all points of discontinuity. Since every
contains all points at which the jump is positive and hence contains all points of discontinuity. Since every 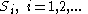 is at most countable, we have that
is at most countable, we have that 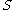 is at most countable.
is at most countable.
If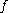 is decreasing
is decreasing
the proof is similar.
If the interval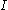 is not closed
is not closed
and bounded
(and hence by Heine-Borel theorem not compact) then the interval can be written as a countable union of closed and bounded intervals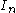 with the property that any two consecutive intervals have an endpoint in common:
with the property that any two consecutive intervals have an endpoint in common: 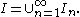
If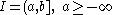 then
then 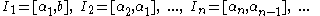 where
where 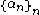 is a strictly decreasing sequence
is a strictly decreasing sequence
such that In a similar way if
In a similar way if 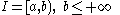 or if
or if 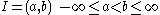 .
.
In any interval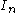 we have at most countable many points of discontinuity, and since a countable union of at most countable sets is at most countable, it follows that the set of all discontinuities is at most countable.
we have at most countable many points of discontinuity, and since a countable union of at most countable sets is at most countable, it follows that the set of all discontinuities is at most countable.
Let f be a monotone function defined on an interval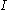 . Then the set of discontinuities is at most countable.
. Then the set of discontinuities is at most countable.
Let f be a monotone function defined on an interval I. Then the set of discontinuities of f is at most countable.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Froda's theorem, named after Alexandru Froda
Alexandru Froda
Alexandru Froda was a well-known Romanian mathematician with important contributions in the field of mathematical analysis, algebra, number theory and rational mechanics. In his 1929 thesis he proved what is now known as Froda's theorem.-Life:Alexandru Froda was born in Bucharest in 1894...
, describes the set of discontinuities of a (monotone) real-valued function
Real-valued function
In mathematics, a real-valued function is a function that associates to every element of the domain a real number in the image....
of a real variable. Usually, this theorem appears in literature without Froda's name being mentioned. However, this result was first proven by A. Froda in 1929.
Definitions
- Consider a function
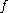 of real variable
of real variable  with real values defined in a neighborhood of a point
with real values defined in a neighborhood of a point 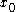 and the function
and the function 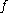 is discontinuous at the point on the real axis
is discontinuous at the point on the real axis 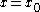 . We will call a removable discontinuity or a jump discontinuity a discontinuity of the first kind.
. We will call a removable discontinuity or a jump discontinuity a discontinuity of the first kind. - Denote
 and
and 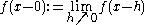 . Then if
. Then if 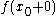 and
and 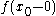 are finite we will call the difference
are finite we will call the difference 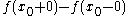 the jump of f at
the jump of f at  .
.
It is obvious that if the function is continuous at
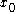 then the jump at
then the jump at 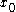 is zero. Moreover, if
is zero. Moreover, if 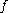 is not continuous in
is not continuous in 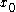 , the jump can be zero at
, the jump can be zero at 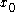 if
if 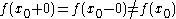 .
.Precise statement
Let f be a monotone function defined on an interval I. Then the set of discontinuities of the first kind is at most countable.Proof
Let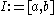 be an interval and
be an interval and 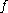 defined on
defined on 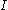 an increasing
an increasingMonotonic function
In mathematics, a monotonic function is a function that preserves the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory....
function. We have
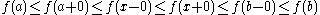
for any
 . Let
. Let  and let
and let 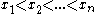 be
be  points inside
points inside 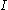 at which the jump of
at which the jump of 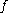 is greater or equal to
is greater or equal to  :
:
We have
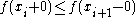 or
or 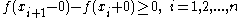 .
.Then
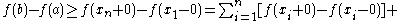
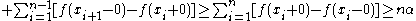
and hence:
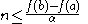 .
.Since
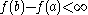 we have that the number of points at which the jump is greater than
we have that the number of points at which the jump is greater than  is finite or zero.
is finite or zero.We define the following sets:
 ,
,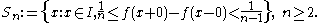
We have that each set
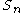 is finite or the empty set
is finite or the empty setEmpty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
. The union
 contains all points at which the jump is positive and hence contains all points of discontinuity. Since every
contains all points at which the jump is positive and hence contains all points of discontinuity. Since every 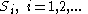 is at most countable, we have that
is at most countable, we have that 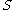 is at most countable.
is at most countable.If
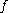 is decreasing
is decreasingMonotonic function
In mathematics, a monotonic function is a function that preserves the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory....
the proof is similar.
If the interval
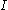 is not closed
is not closedClosed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
and bounded
Bounded set
In mathematical analysis and related areas of mathematics, a set is called bounded, if it is, in a certain sense, of finite size. Conversely, a set which is not bounded is called unbounded...
(and hence by Heine-Borel theorem not compact) then the interval can be written as a countable union of closed and bounded intervals
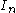 with the property that any two consecutive intervals have an endpoint in common:
with the property that any two consecutive intervals have an endpoint in common: 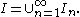
If
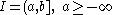 then
then 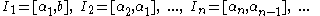 where
where 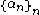 is a strictly decreasing sequence
is a strictly decreasing sequenceSequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
such that
 In a similar way if
In a similar way if 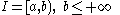 or if
or if 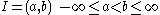 .
.In any interval
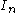 we have at most countable many points of discontinuity, and since a countable union of at most countable sets is at most countable, it follows that the set of all discontinuities is at most countable.
we have at most countable many points of discontinuity, and since a countable union of at most countable sets is at most countable, it follows that the set of all discontinuities is at most countable.Remark
One can prove that all points of discontinuity of a monotone real-valued function defined on an interval are either removable or jump discontinuities and hence, by our definition, of the first kind. With this remark Froda's theorem takes the stronger form:Let f be a monotone function defined on an interval
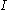 . Then the set of discontinuities is at most countable.
. Then the set of discontinuities is at most countable.See also
- Continuous functionContinuous functionIn mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
- Classification of discontinuitiesClassification of discontinuitiesContinuous functions are of utmost importance in mathematics and applications. However, not all functions are continuous. If a function is not continuous at a point in its domain, one says that it has a discontinuity there...
Let f be a monotone function defined on an interval I. Then the set of discontinuities of f is at most countable.

