Erdos–Stone theorem
Encyclopedia
In extremal graph theory
, the Erdős–Stone theorem is an asymptotic result generalising Turán's theorem
to bound the number of edges in an H-free graph for a non-complete graph H. It is named after Paul Erdős
and Arthur Stone, who proved it in 1946, and it has been described as the “fundamental theorem of extremal graph theory”.
The extremal function ex(n; H) is defined to be the maximum number of edges in a graph of order n not containing a subgraph isomorphic to H. Turán's theorem says that ex(n; Kr) = tr − 1(n), the order of the Turán graph
, and that the Turán graph is the unique extremal graph. The Erdős-Stone theorem extends this to Kr(t), the complete r-partite graph with t vertices in each class, or equivalently the Turán graph
T(rt,r):
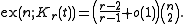
An immediate corollary is that this applies to any graph H with chromatic number r, since such a graph is contained in Kr(t) for sufficiently large t but is not contained in any Turán graph Tr-1(n). For bipartite graphs H, however, the theorem gives only the limited information that ex(n; H) = o(n2), and for general bipartite graphs little more is known.
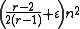
contains a Kr(t).
Erdős and Stone proved that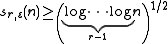
for n sufficiently large. The correct order of sr,ε(n) in terms of n was found by Bollobás and Erdős: for any given r and ε there are constants c1(r, ε) and c2(r, ε) such that c1(r, ε) log n < sr,ε(n) < c2(r, ε) log n. Chvátal and Szemerédi then determined the nature of the dependence on r and ε, up to a constant: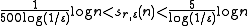
for sufficiently large n.
Extremal graph theory
Extremal graph theory is a branch of the mathematical field of graph theory. Extremal graph theory studies extremal graphs which satisfy a certain property. Extremality can be taken with respect to different graph invariants, such as order, size or girth...
, the Erdős–Stone theorem is an asymptotic result generalising Turán's theorem
Turán's theorem
In graph theory, Turán's theorem is a result on the number of edges in a Kr+1-free graph.An n-vertex graph that does not contain any -vertex clique may be formed by partitioning the set of vertices into r parts of equal or nearly-equal size, and connecting two vertices by an edge whenever they...
to bound the number of edges in an H-free graph for a non-complete graph H. It is named after Paul Erdős
Paul Erdos
Paul Erdős was a Hungarian mathematician. Erdős published more papers than any other mathematician in history, working with hundreds of collaborators. He worked on problems in combinatorics, graph theory, number theory, classical analysis, approximation theory, set theory, and probability theory...
and Arthur Stone, who proved it in 1946, and it has been described as the “fundamental theorem of extremal graph theory”.
The extremal function ex(n; H) is defined to be the maximum number of edges in a graph of order n not containing a subgraph isomorphic to H. Turán's theorem says that ex(n; Kr) = tr − 1(n), the order of the Turán graph
Turán graph
The Turán graph T is a graph formed by partitioning a set of n vertices into r subsets, with sizes as equal as possible, and connecting two vertices by an edge whenever they belong to different subsets. The graph will have subsets of size \lceil n/r\rceil, and r- subsets of size \lfloor n/r\rfloor...
, and that the Turán graph is the unique extremal graph. The Erdős-Stone theorem extends this to Kr(t), the complete r-partite graph with t vertices in each class, or equivalently the Turán graph
Turán graph
The Turán graph T is a graph formed by partitioning a set of n vertices into r subsets, with sizes as equal as possible, and connecting two vertices by an edge whenever they belong to different subsets. The graph will have subsets of size \lceil n/r\rceil, and r- subsets of size \lfloor n/r\rfloor...
T(rt,r):
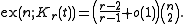
An immediate corollary is that this applies to any graph H with chromatic number r, since such a graph is contained in Kr(t) for sufficiently large t but is not contained in any Turán graph Tr-1(n). For bipartite graphs H, however, the theorem gives only the limited information that ex(n; H) = o(n2), and for general bipartite graphs little more is known.
Quantitative results
Several versions of the theorem have been proved that more precisely characterise the relation of n, r, t and the o(1) term. Define the notation sr,ε(n) (for 0 < ε < 1/(2(r − 1))) to be the greatest t such that every graph of order n and size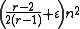contains a Kr(t).
Erdős and Stone proved that
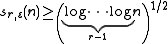
for n sufficiently large. The correct order of sr,ε(n) in terms of n was found by Bollobás and Erdős: for any given r and ε there are constants c1(r, ε) and c2(r, ε) such that c1(r, ε) log n < sr,ε(n) < c2(r, ε) log n. Chvátal and Szemerédi then determined the nature of the dependence on r and ε, up to a constant:
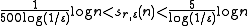for sufficiently large n.