A point is said to be equidistant from a set of objects if the distance

Distance

Distance is a numerical description of how far apart objects are. In physics or everyday discussion, distance may refer to a physical length, or an estimation based on other criteria . In mathematics, a distance function or metric is a generalization of the concept of physical distance...

s between that point and each object in the set are equal.

In two-dimensional Euclidian geometry the locus

Locus (mathematics)

In geometry, a locus is a collection of points which share a property. For example a circle may be defined as the locus of points in a plane at a fixed distance from a given point....

 of points equidistant from two given (different) points is their perpendicular bisector. In three dimensions, the locus of points equidistant from two given points is a plane, and generalising further, in n-dimensional space the locus of points equidistant from two points in n-space

N-Space

n-Space is an American video game developer founded in 1994 by Erick S. Dyke, Dan O'Leary, and Sean Purcell. n-Space is focusing mostly on Nintendo consoles since 2001...

 is an (n−1)-space.

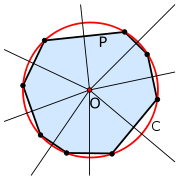
For a triangle the circumcentre is a point equidistant from each of the three end points. Every non degenerate triangle has such a point. This result can be generalised to cyclic polygons. The center of a circle is equidistant from every point on the circle. Likewise the center of a sphere

Sphere

A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...

 is equidistant from every point on the sphere.

A parabola

Parabola

In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...

 is the set of points in a plane equidistant from a fixed point (the focus) and a fixed line (the directrix), where distance from the directrix is measured along a line perpendicular to the directrix.

In shape analysis

Shape analysis

This article describes shape analysis to analyze and process geometric shapes.The shape analysis described here is related to the statistical analysis of geometric shapes, to shape matching and shape recognition...

, the topological skeleton

Topological skeleton

In shape analysis, skeleton of a shape is a thin version of that shape that is equidistant to its boundaries. The skeleton usually emphasizes geometrical and topological properties of the shape, such as its connectivity, topology, length, direction, and width...

 or medial axis of a shape

Shape

The shape of an object located in some space is a geometrical description of the part of that space occupied by the object, as determined by its external boundary – abstracting from location and orientation in space, size, and other properties such as colour, content, and material...

 is a thin version of that shape that is equidistant from its boundaries

Boundary (topology)

In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...

.