Elliptic cohomology
Encyclopedia
In mathematics
, elliptic cohomology is a cohomology theory in the sense of algebraic topology
. It is related to elliptic curves and modular forms.
 acts smoothly and non-trivially on a spin manifold, then the index of the Dirac operator
acts smoothly and non-trivially on a spin manifold, then the index of the Dirac operator
vanishes. In 1983, Witten
conjectured that in this situation the equivariant index of a certain twisted Dirac operator is at least constant. This led to certain other problems concerning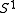 -actions on manifolds, which could be solved by Ochanine by the introduction of elliptic genera. These got in turn by Witten related to (conjectural) index theory on free loop
-actions on manifolds, which could be solved by Ochanine by the introduction of elliptic genera. These got in turn by Witten related to (conjectural) index theory on free loop
spaces. Elliptic cohomology, invented in its original form by Landweber, Stong and Ravenel
in the late 1980s, was introduced to clarify certain issues with elliptic genera and provide a context for (conjectural) index theory of families of differential operators on free loop spaces. In some sense it can be seen as an approximation to the K-theory
of the free loop space.
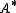 even periodic if
even periodic if 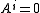 for i odd and there is an invertible element
for i odd and there is an invertible element 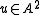 . These theories possess a complex orientation, which gives a formal group law. A particular rich source for formal group laws are elliptic curve
. These theories possess a complex orientation, which gives a formal group law. A particular rich source for formal group laws are elliptic curve
s. A cohomology theory A with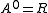 is called elliptic if it is even periodic and its formal group law is isomorphic to a formal group law of an elliptic curve E over R. The usual construction of such elliptic cohomology theories uses the Landweber exact functor theorem
is called elliptic if it is even periodic and its formal group law is isomorphic to a formal group law of an elliptic curve E over R. The usual construction of such elliptic cohomology theories uses the Landweber exact functor theorem
. If the formal group laws of E is Landweber exact, one can define an elliptic cohomology theory (on finite complexes) by
Franke has identified the condition needed to fulfill Landweber exactness:
These conditions can be checked in many cases related to elliptic genera. Moreover, the conditions are fulfilled in the universal case in the sense that the map from the moduli stack of elliptic curves to the moduli stack of formal group
s is flat
is flat
. This gives then a presheaf of cohomology theories over the site of affine schemes flat over the moduli stack of elliptic curves. The desire to get a universal elliptic cohomology theory by taking global sections has led to the construction of the topological modular forms
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, elliptic cohomology is a cohomology theory in the sense of algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
. It is related to elliptic curves and modular forms.
History and motivation
Historically, elliptic cohomology arose from the study of elliptic genera. It is known by Atiyah and Hirzebruch that if acts smoothly and non-trivially on a spin manifold, then the index of the Dirac operator
acts smoothly and non-trivially on a spin manifold, then the index of the Dirac operatorDirac operator
In mathematics and quantum mechanics, a Dirac operator is a differential operator that is a formal square root, or half-iterate, of a second-order operator such as a Laplacian...
vanishes. In 1983, Witten
Edward Witten
Edward Witten is an American theoretical physicist with a focus on mathematical physics who is currently a professor of Mathematical Physics at the Institute for Advanced Study....
conjectured that in this situation the equivariant index of a certain twisted Dirac operator is at least constant. This led to certain other problems concerning
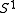 -actions on manifolds, which could be solved by Ochanine by the introduction of elliptic genera. These got in turn by Witten related to (conjectural) index theory on free loop
-actions on manifolds, which could be solved by Ochanine by the introduction of elliptic genera. These got in turn by Witten related to (conjectural) index theory on free loopFree loop
In the mathematical field of topology, a free loop is a variant of the mathematical notion of a loop. Whereas a loop has a distinguished point on it, called a basepoint, a free loop lacks such a distinguished point. Formally, let X be a topological space. Then a free loop in X is an equivalence...
spaces. Elliptic cohomology, invented in its original form by Landweber, Stong and Ravenel
Douglas Ravenel
Douglas Conner Ravenel is an American mathematician known for work in algebraic topology.-Life:He received his Ph.D. from Brandeis University in 1972 under the direction of Edgar H. Brown, Jr. with a thesis on exotic characteristic classes of spherical fibrations. From 1971 to 1973 he was...
in the late 1980s, was introduced to clarify certain issues with elliptic genera and provide a context for (conjectural) index theory of families of differential operators on free loop spaces. In some sense it can be seen as an approximation to the K-theory
Topological K-theory
In mathematics, topological K-theory is a branch of algebraic topology. It was founded to study vector bundles on general topological spaces, by means of ideas now recognised as K-theory that were introduced by Alexander Grothendieck...
of the free loop space.
Definitions and constructions
Call a cohomology theory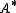 even periodic if
even periodic if 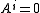 for i odd and there is an invertible element
for i odd and there is an invertible element 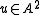 . These theories possess a complex orientation, which gives a formal group law. A particular rich source for formal group laws are elliptic curve
. These theories possess a complex orientation, which gives a formal group law. A particular rich source for formal group laws are elliptic curveElliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
s. A cohomology theory A with
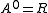 is called elliptic if it is even periodic and its formal group law is isomorphic to a formal group law of an elliptic curve E over R. The usual construction of such elliptic cohomology theories uses the Landweber exact functor theorem
is called elliptic if it is even periodic and its formal group law is isomorphic to a formal group law of an elliptic curve E over R. The usual construction of such elliptic cohomology theories uses the Landweber exact functor theoremLandweber exact functor theorem
In mathematics, the Landweber exact functor theorem, named after Peter Landweber, is an important theorem in algebraic topology. It is known that a complex orientation of a homology theory leads to a formal group law...
. If the formal group laws of E is Landweber exact, one can define an elliptic cohomology theory (on finite complexes) by
Franke has identified the condition needed to fulfill Landweber exactness:
- R needs to be flat over
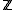
- There is no irreducible component X of
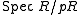 , where the fiber
, where the fiber  is supersingular for every
is supersingular for every 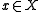
These conditions can be checked in many cases related to elliptic genera. Moreover, the conditions are fulfilled in the universal case in the sense that the map from the moduli stack of elliptic curves to the moduli stack of formal group
Formal group
In mathematics, a formal group law is a formal power series behaving as if it were the product of a Lie group. They were introduced by . The term formal group sometimes means the same as formal group law, and sometimes means one of several generalizations. Formal groups are intermediate between...
s
 is flat
is flatFlat morphism
In mathematics, in particular in the theory of schemes in algebraic geometry, a flat morphism f from a scheme X to a scheme Y is a morphism such that the induced map on every stalk is a flat map of rings, i.e.,is a flat map for all P in X...
. This gives then a presheaf of cohomology theories over the site of affine schemes flat over the moduli stack of elliptic curves. The desire to get a universal elliptic cohomology theory by taking global sections has led to the construction of the topological modular forms
Topological modular forms
In mathematics, the spectrum of topological modular forms describes a generalized cohomology theory whose coefficient ring is related to the graded ring of holomorphic modular forms with integral cusp expansions...
.