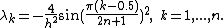Eigenvalues and eigenvectors of the second derivative
Encyclopedia
Explicit formulas for eigenvalues and eigenvectors of the second derivative
with different boundary conditions are provided both for the continuous and discrete cases. In the discrete case, the standard central difference approximation of the second derivative is used on a uniform grid.
These formulas are used to derive the expressions for eigenfunctions of Laplacian in case of separation of variables
, as well as to find eigenvalues and eigenvectors of multidimensional discrete Laplacian
on a regular grid
, which is presented as a Kronecker sum of discrete Laplacians
in one-dimension.
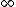 . Assuming the equation is defined on the domain
. Assuming the equation is defined on the domain 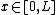 , the following are the eigenvalues and normalized eigenvectors. The eigenvalues are ordered in descending order.
, the following are the eigenvalues and normalized eigenvectors. The eigenvalues are ordered in descending order.
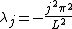
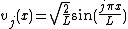
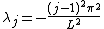
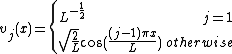
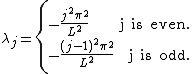
(Note that eigenvalues are repeated except for 0 eigenvalue.)
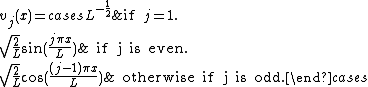
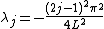

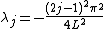
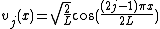



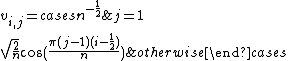
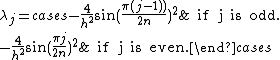
(Note that eigenvalues are repeated except for 0 and the largest one if n is even.)
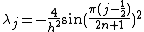
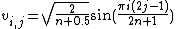
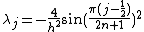

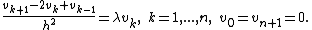
Rearranging terms, we get
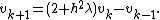
Now let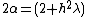 . Also, assuming
. Also, assuming 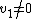 , we can scale eigenvectors by any nonzero scalar, so scale
, we can scale eigenvectors by any nonzero scalar, so scale  so that
so that 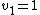 .
.
Then we find the recurrence
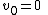
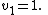

Considering as an indeterminate,
as an indeterminate,
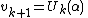
where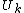 is the kth Chebyshev polynomial
is the kth Chebyshev polynomial
of the 2nd kind.
Since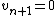 , we get that
, we get that
 .
.
It is clear that the eigenvalues of our problem will be the zeros of the nth Chebyshev polynomial of the second kind, with the relation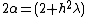 .
.
These zeros are well known and are:
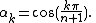
Plugging these into the formula for ,
,

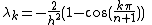
And using a trig formula to simplify, we find
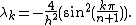

In the standard discretization, we introduce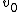 and
and  and define
and define
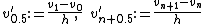
The boundary conditions are then equivalent to
If we make a change of variables,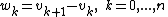
we can derive the following: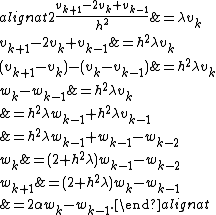
with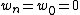 being the boundary conditions.
being the boundary conditions.
This is precisely the Dirichlet formula with interior grid points and grid spacing
interior grid points and grid spacing 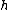 . Similar to what we saw in the above, assuming
. Similar to what we saw in the above, assuming 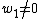 , we get
, we get
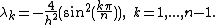
This gives us eigenvalues and there are
eigenvalues and there are  . If we drop the assumption that
. If we drop the assumption that 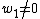 , we find there is also a solution with
, we find there is also a solution with 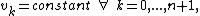 and this corresponds to eigenvalue
and this corresponds to eigenvalue  .
.
Relabeling the indices in the formula above and combining with the zero eigenvalue, we obtain,
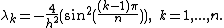
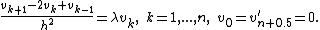 ,
,
where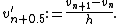
We need to introduce auxiliary variables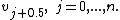
Consider the recurrence
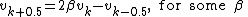 .
.
Also, we know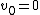 and assuming
and assuming  , we can scale
, we can scale 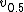 so that
so that 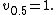
We can also write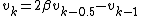

Taking the correct combination of these three equations, we can obtain
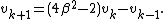
And thus our new recurrence will solve our eigenvalue problem when
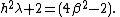
Solving for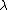 we get
we get

Our new recurrence gives
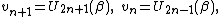
where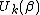 again is the kth Chebyshev polynomial
again is the kth Chebyshev polynomial
of the 2nd kind.
And combining with our Neumann boundary condition, we have

A well-known formula relates the Chebyshev polynomials
of the first kind,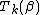 , to those of the second kind by
, to those of the second kind by
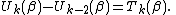
Thus our eigenvalues solve
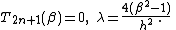
The zeros of this polynomial are also known to be
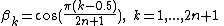
And thus
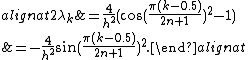
Note that there are 2n + 1 of these values, but only the first n + 1 are unique. The (n + 1)th value gives us the zero vector as an eigenvector with eigenvalue 0, which is trivial. This can be seen by returning to the original recurrence. So we consider only the first n of these values to be the n eigenvalues of the Dirichlet - Neumann problem.
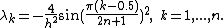
Second derivative
In calculus, the second derivative of a function ƒ is the derivative of the derivative of ƒ. Roughly speaking, the second derivative measures how the rate of change of a quantity is itself changing; for example, the second derivative of the position of a vehicle with respect to time is...
with different boundary conditions are provided both for the continuous and discrete cases. In the discrete case, the standard central difference approximation of the second derivative is used on a uniform grid.
These formulas are used to derive the expressions for eigenfunctions of Laplacian in case of separation of variables
Separation of variables
In mathematics, separation of variables is any of several methods for solving ordinary and partial differential equations, in which algebra allows one to rewrite an equation so that each of two variables occurs on a different side of the equation....
, as well as to find eigenvalues and eigenvectors of multidimensional discrete Laplacian
Discrete Laplace operator
In mathematics, the discrete Laplace operator is an analog of the continuous Laplace operator, defined so that it has meaning on a graph or a discrete grid...
on a regular grid
Regular grid
A regular grid is a tessellation of n-dimensional Euclidean space by congruent parallelotopes . Grids of this type appear on graph paper and may be used in finite element analysis as well as finite volume methods and finite difference methods...
, which is presented as a Kronecker sum of discrete Laplacians
Kronecker sum of discrete Laplacians
In mathematics, the Kronecker sum of discrete Laplacians, named after Leopold Kronecker, is a discrete version of the separation of variables for the continuous Laplacian in a rectangular cuboid domain.-General form of the Kronecker sum of discrete Laplacians:...
in one-dimension.
The continuous case
The index j represents the jth eigenvalue or eigenvector and runs from 1 to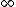 . Assuming the equation is defined on the domain
. Assuming the equation is defined on the domain 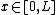 , the following are the eigenvalues and normalized eigenvectors. The eigenvalues are ordered in descending order.
, the following are the eigenvalues and normalized eigenvectors. The eigenvalues are ordered in descending order.Pure Dirichlet boundary conditions
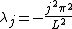
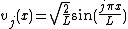
Pure Neumann boundary conditions
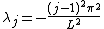
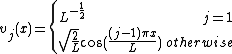
Periodic boundary conditions
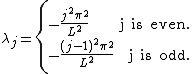
(Note that eigenvalues are repeated except for 0 eigenvalue.)
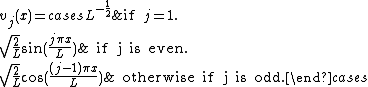
Mixed Dirichlet-Neumann boundary conditions
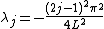

Mixed Neumann-Dirichlet boundary conditions
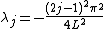
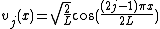
The discrete case
Notation: The index j represents the jth eigenvalue or eigenvector. The index i represents the ith component of an eigenvector. Both i and j go from 1 to n, where the matrix is size n x n. Eigenvectors are normalized. The eigenvalues are ordered in descending order.Pure Dirichlet boundary conditions


Pure Neumann boundary conditions

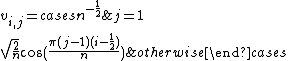
Periodic boundary conditions
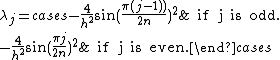
(Note that eigenvalues are repeated except for 0 and the largest one if n is even.)

Mixed Dirichlet-Neumann boundary conditions
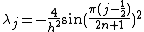
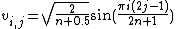
Mixed Neumann-Dirichlet boundary conditions
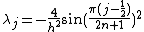

Dirichlet case
In the 1D discrete case with Dirichlet boundary conditions, we are solving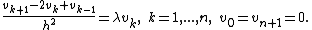
Rearranging terms, we get
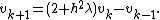
Now let
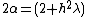 . Also, assuming
. Also, assuming 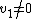 , we can scale eigenvectors by any nonzero scalar, so scale
, we can scale eigenvectors by any nonzero scalar, so scale  so that
so that 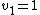 .
.Then we find the recurrence
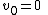
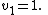

Considering
 as an indeterminate,
as an indeterminate,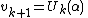
where
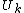 is the kth Chebyshev polynomial
is the kth Chebyshev polynomialChebyshev polynomials
In mathematics the Chebyshev polynomials, named after Pafnuty Chebyshev, are a sequence of orthogonal polynomials which are related to de Moivre's formula and which can be defined recursively. One usually distinguishes between Chebyshev polynomials of the first kind which are denoted Tn and...
of the 2nd kind.
Since
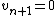 , we get that
, we get that .
.It is clear that the eigenvalues of our problem will be the zeros of the nth Chebyshev polynomial of the second kind, with the relation
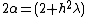 .
.These zeros are well known and are:
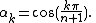
Plugging these into the formula for
 ,
,
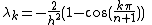
And using a trig formula to simplify, we find
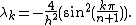
Neumann case
In the Neumann case, we are solving
In the standard discretization, we introduce
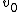 and
and  and define
and define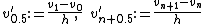
The boundary conditions are then equivalent to

If we make a change of variables,
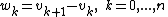
we can derive the following:
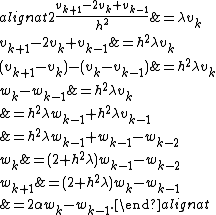
with
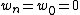 being the boundary conditions.
being the boundary conditions.This is precisely the Dirichlet formula with
 interior grid points and grid spacing
interior grid points and grid spacing 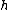 . Similar to what we saw in the above, assuming
. Similar to what we saw in the above, assuming 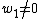 , we get
, we get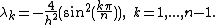
This gives us
 eigenvalues and there are
eigenvalues and there are  . If we drop the assumption that
. If we drop the assumption that 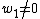 , we find there is also a solution with
, we find there is also a solution with 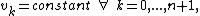 and this corresponds to eigenvalue
and this corresponds to eigenvalue  .
.Relabeling the indices in the formula above and combining with the zero eigenvalue, we obtain,
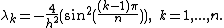
Dirichlet-Neumann Case
For the Dirichlet-Neumann case, we are solving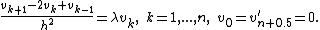 ,
,where
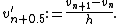
We need to introduce auxiliary variables
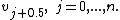
Consider the recurrence
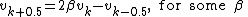 .
.Also, we know
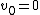 and assuming
and assuming  , we can scale
, we can scale 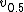 so that
so that 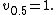
We can also write
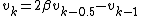

Taking the correct combination of these three equations, we can obtain
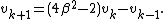
And thus our new recurrence will solve our eigenvalue problem when
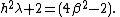
Solving for
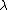 we get
we get
Our new recurrence gives
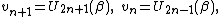
where
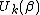 again is the kth Chebyshev polynomial
again is the kth Chebyshev polynomialChebyshev polynomials
In mathematics the Chebyshev polynomials, named after Pafnuty Chebyshev, are a sequence of orthogonal polynomials which are related to de Moivre's formula and which can be defined recursively. One usually distinguishes between Chebyshev polynomials of the first kind which are denoted Tn and...
of the 2nd kind.
And combining with our Neumann boundary condition, we have

A well-known formula relates the Chebyshev polynomials
Chebyshev polynomials
In mathematics the Chebyshev polynomials, named after Pafnuty Chebyshev, are a sequence of orthogonal polynomials which are related to de Moivre's formula and which can be defined recursively. One usually distinguishes between Chebyshev polynomials of the first kind which are denoted Tn and...
of the first kind,
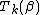 , to those of the second kind by
, to those of the second kind by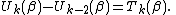
Thus our eigenvalues solve
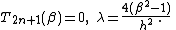
The zeros of this polynomial are also known to be
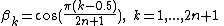
And thus
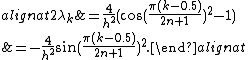
Note that there are 2n + 1 of these values, but only the first n + 1 are unique. The (n + 1)th value gives us the zero vector as an eigenvector with eigenvalue 0, which is trivial. This can be seen by returning to the original recurrence. So we consider only the first n of these values to be the n eigenvalues of the Dirichlet - Neumann problem.