
Dynamical mean field theory
Encyclopedia
Dynamical Mean Field Theory (DMFT) is a method to determine the electronic structure of strongly correlated materials. In such materials, the approximation of independent electrons, which is used in Density Functional Theory
and usual band structure calculations, breaks down. Dynamical Mean-Field Theory, a non-perturbative treatment of local interactions between electrons, bridges the gap between the nearly-free electron
gas limit and the atomic limit of condensed-matter physics.
DMFT consists in mapping a many-body
lattice problem to a many-body local problem, called an impurity model. While the lattice problem is in general intractable, the impurity model is usually solvable through various schemes. The mapping in itself does not constitute an approximation. The only approximation made in ordinary DMFT schemes is to assume the lattice self-energy
to be a momentum-independent (local) quantity. This approximation becomes exact in the limit of lattices with an infinite coordination
.
One of DMFT's main successes is to describe the phase transition
between a metal and a Mott insulator
when the strength of electronic correlation
s is increased. It has been successfully applied to real materials, in combination to the local density approximation of Density Functional Theory.
. In the Ising model, the lattice problem is mapped onto an effective single site problem, whose magnetization is to reproduce the lattice magnetization through an effective "mean-field". This condition is called the self-consistency condition. It stipulates that the single-site observables should reproduce the lattice "local" observables by means of an effective field. While the N-site Ising Hamiltonian is hard to solve analytically (to date, analytical solutions exist only for the 1D and 2D case), the single-site problem is easily solved.
Likewise, DMFT maps a lattice problem (e.g the Hubbard model
) onto a single-site problem. In DMFT, the local observable is the local Green's function
. Thus, the self-consistency condition for DMFT is for the impurity Green's function to reproduce the lattice local Green's function through an effective mean-field which, in DMFT, is the hybridization function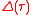 of the impurity model. DMFT owes its name to the fact that the mean-field
of the impurity model. DMFT owes its name to the fact that the mean-field  is time-dependent, or dynamical. This also points to the major difference between the Ising MFT and DMFT: Ising MFT maps the N-spin problem into a single-site, single-spin problem. DMFT maps the lattice problem onto a single-site problem, but the latter fundamentally remains a N-body problem which captures the temporal fluctuations due to electron-electron correlations.
is time-dependent, or dynamical. This also points to the major difference between the Ising MFT and DMFT: Ising MFT maps the N-spin problem into a single-site, single-spin problem. DMFT maps the lattice problem onto a single-site problem, but the latter fundamentally remains a N-body problem which captures the temporal fluctuations due to electron-electron correlations.
 . The Hubbard Hamiltonian may take the following form:
. The Hubbard Hamiltonian may take the following form:
where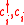 denote the creation and annihilation operators of an electron on a localized orbital on site
denote the creation and annihilation operators of an electron on a localized orbital on site  , and
, and 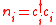 .
.
The following assumptions have been made:
(AIM). This model describes the interaction of one site (the impurity) with a "bath" of electronic levels (described by the annihilation and creation operators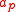 and
and 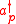 ) through an hybridization function. The Anderson model corresponding to our single-site model is a single-orbital Anderson impurity model, whose hamiltonian formulation is the following:
) through an hybridization function. The Anderson model corresponding to our single-site model is a single-orbital Anderson impurity model, whose hamiltonian formulation is the following: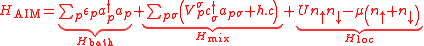
where
The Matsubara Green's function of this model, defined by , is entirely determined by the parameters
, is entirely determined by the parameters 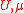 and the so-called hybridization function
and the so-called hybridization function  , which is the imaginary-time Fourier-transform of
, which is the imaginary-time Fourier-transform of 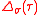 .
.
This hybridization function describes the dynamics of electrons hopping in and out of the bath. It should reproduce the lattice dynamics such that the impurity Green's function is the same as the local lattice Green's function. It is related to the non-interacting Green's function by the relation: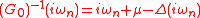 (1)
(1)
Solving the Anderson impurity model consists in computing observables such as the interacting Green's function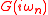 for a given hybridization function
for a given hybridization function  and
and 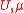 . It is a difficult but not intractable problem. There exists a number of ways to solve the AIM, such as
. It is a difficult but not intractable problem. There exists a number of ways to solve the AIM, such as
 to coincide with the local lattice Green's function
to coincide with the local lattice Green's function 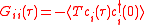 :
: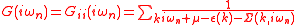
where denotes the lattice self-energy.
denotes the lattice self-energy.
, by equating it to the impurity self-energy: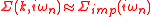
This approximation becomes exact in the limit of lattices with infinite coordination, that is when the number of neighbors of each site is infinite. Indeed, one can show that in the diagrammatic expansion of the lattice self-energy, only local diagrams survive when one goes into the infinite coordination limit.
Thus, as in classical mean-field theories, DMFT is supposed to get more accurate as the dimensionality (and thus the number of neighbors) increases. Other put, for low dimensions, spatial fluctuations will render the DMFT approximation less reliable.
 ,
,  and temperature
and temperature 
Self-consistency is reached when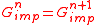 .
.
 , bandwidth, filling (chemical potential
, bandwidth, filling (chemical potential  ), and temperature
), and temperature  :
:
In particular, the drop of the double-occupancy as increases is a signature of the Mott transition.
increases is a signature of the Mott transition.
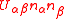 where
where  and
and  denote different orbitals. This is especially relevant for compounds whose
denote different orbitals. This is especially relevant for compounds whose  -orbitals are degenerate, such as iron in the newly discovered high-temperature iron-based superconductor
-orbitals are degenerate, such as iron in the newly discovered high-temperature iron-based superconductor
s (pnictides).
Density functional theory
Density functional theory is a quantum mechanical modelling method used in physics and chemistry to investigate the electronic structure of many-body systems, in particular atoms, molecules, and the condensed phases. With this theory, the properties of a many-electron system can be determined by...
and usual band structure calculations, breaks down. Dynamical Mean-Field Theory, a non-perturbative treatment of local interactions between electrons, bridges the gap between the nearly-free electron
Nearly-free electron model
In solid-state physics, the nearly-free electron model is a quantum mechanical model of physical properties of electrons that can move almost freely through the crystal lattice of a solid. The model is closely related to the more conceptual Empty Lattice Approximation...
gas limit and the atomic limit of condensed-matter physics.
DMFT consists in mapping a many-body
Many-body problem
The many-body problem is a general name for a vast category of physical problems pertaining to the properties of microscopic systems made of a large number of interacting particles. Microscopic here implies that quantum mechanics has to be used to provide an accurate description of the system...
lattice problem to a many-body local problem, called an impurity model. While the lattice problem is in general intractable, the impurity model is usually solvable through various schemes. The mapping in itself does not constitute an approximation. The only approximation made in ordinary DMFT schemes is to assume the lattice self-energy
Self-energy
In theoretical physics and quantum field theory a particle's self-energy \Sigma represents the contribution to the particle's energy, or effective mass, due to interactions between the particle and the system it is part of...
to be a momentum-independent (local) quantity. This approximation becomes exact in the limit of lattices with an infinite coordination
Coordination number
In chemistry and crystallography, the coordination number of a central atom in a molecule or crystal is the number of its nearest neighbours. This number is determined somewhat differently for molecules and for crystals....
.
One of DMFT's main successes is to describe the phase transition
Phase transition
A phase transition is the transformation of a thermodynamic system from one phase or state of matter to another.A phase of a thermodynamic system and the states of matter have uniform physical properties....
between a metal and a Mott insulator
Mott insulator
Mott insulators are a class of materials that should conduct electricity under conventional band theories, but are insulators when measured...
when the strength of electronic correlation
Electronic correlation
Electronic correlation is the interaction between electrons in the electronic structure of a quantum system.- Atomic and molecular systems :...
s is increased. It has been successfully applied to real materials, in combination to the local density approximation of Density Functional Theory.
Relation to Mean-Field Theory
The DMFT treatment of lattice quantum models is similar to the mean-field theory (MFT) treatment of classical models such as the Ising modelIsing model
The Ising model is a mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables called spins that can be in one of two states . The spins are arranged in a graph , and each spin interacts with its nearest neighbors...
. In the Ising model, the lattice problem is mapped onto an effective single site problem, whose magnetization is to reproduce the lattice magnetization through an effective "mean-field". This condition is called the self-consistency condition. It stipulates that the single-site observables should reproduce the lattice "local" observables by means of an effective field. While the N-site Ising Hamiltonian is hard to solve analytically (to date, analytical solutions exist only for the 1D and 2D case), the single-site problem is easily solved.
Likewise, DMFT maps a lattice problem (e.g the Hubbard model
Hubbard model
The Hubbard model is an approximate model used, especially in solid state physics, to describe the transition between conducting and insulating systems...
) onto a single-site problem. In DMFT, the local observable is the local Green's function
Green's function (many-body theory)
In many-body theory, the term Green's function is sometimes used interchangeably with correlation function, but refers specifically to correlators of field operators or creation and annihilation operators....
. Thus, the self-consistency condition for DMFT is for the impurity Green's function to reproduce the lattice local Green's function through an effective mean-field which, in DMFT, is the hybridization function
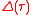 of the impurity model. DMFT owes its name to the fact that the mean-field
of the impurity model. DMFT owes its name to the fact that the mean-field  is time-dependent, or dynamical. This also points to the major difference between the Ising MFT and DMFT: Ising MFT maps the N-spin problem into a single-site, single-spin problem. DMFT maps the lattice problem onto a single-site problem, but the latter fundamentally remains a N-body problem which captures the temporal fluctuations due to electron-electron correlations.
is time-dependent, or dynamical. This also points to the major difference between the Ising MFT and DMFT: Ising MFT maps the N-spin problem into a single-site, single-spin problem. DMFT maps the lattice problem onto a single-site problem, but the latter fundamentally remains a N-body problem which captures the temporal fluctuations due to electron-electron correlations.Single-orbital Hubbard model
The Hubbard model describes the onsite interaction between electrons of opposite spin by a single parameter, . The Hubbard Hamiltonian may take the following form:
. The Hubbard Hamiltonian may take the following form:
where
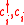 denote the creation and annihilation operators of an electron on a localized orbital on site
denote the creation and annihilation operators of an electron on a localized orbital on site  , and
, and 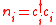 .
.The following assumptions have been made:
- only one orbital contributes to the electronic properties (as might be the case of copper atoms in superconducting cuprates, whose
 -bands are non-degenerate),
-bands are non-degenerate), - the orbitals are so localized that only nearest-neighbor hopping
 is taken into account
is taken into account
The auxiliary problem: the Anderson impurity model
The Hubbard model is in general intractable under usual perturbation expansion techniques. DMFT maps this lattice model onto the so-called Anderson impurity modelAnderson model
The Anderson Impurity Model is a Hamiltonian model that is often used to describe heavy fermion systems and Kondo insulators. The model contains a narrow resonance between a magnetic impurity state and a conduction electron state. The model also contains an on-site repulsion term as found in the...
(AIM). This model describes the interaction of one site (the impurity) with a "bath" of electronic levels (described by the annihilation and creation operators
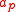 and
and 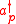 ) through an hybridization function. The Anderson model corresponding to our single-site model is a single-orbital Anderson impurity model, whose hamiltonian formulation is the following:
) through an hybridization function. The Anderson model corresponding to our single-site model is a single-orbital Anderson impurity model, whose hamiltonian formulation is the following: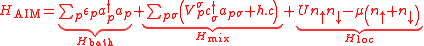
where
-
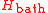 describes the non-correlated electronic levels
describes the non-correlated electronic levels 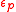 of the bath
of the bath -
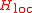 describes the impurity, where two electrons interact with the energetical cost
describes the impurity, where two electrons interact with the energetical cost 
 describes the hybridization (or coupling) between the impurity and the bath through hybridization terms
describes the hybridization (or coupling) between the impurity and the bath through hybridization terms 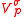
The Matsubara Green's function of this model, defined by
 , is entirely determined by the parameters
, is entirely determined by the parameters 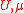 and the so-called hybridization function
and the so-called hybridization function  , which is the imaginary-time Fourier-transform of
, which is the imaginary-time Fourier-transform of 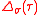 .
.This hybridization function describes the dynamics of electrons hopping in and out of the bath. It should reproduce the lattice dynamics such that the impurity Green's function is the same as the local lattice Green's function. It is related to the non-interacting Green's function by the relation:
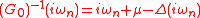 (1)
(1)Solving the Anderson impurity model consists in computing observables such as the interacting Green's function
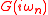 for a given hybridization function
for a given hybridization function  and
and 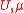 . It is a difficult but not intractable problem. There exists a number of ways to solve the AIM, such as
. It is a difficult but not intractable problem. There exists a number of ways to solve the AIM, such as
- Exact diagonalization
- Hirsch-Fye algorithm
- Iterative Perturbation Theory
- Non-Crossing Approximation
- Continuous-Time Quantum Monte CarloQuantum Monte CarloQuantum Monte Carlo is a large class of computer algorithms that simulate quantum systems with the idea of solving the quantum many-body problem. They use, in one way or another, the Monte Carlo method to handle the many-dimensional integrals that arise...
algorithms
Self-consistency equations
The self-consistency condition requires the impurity Green's function to coincide with the local lattice Green's function
to coincide with the local lattice Green's function 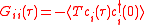 :
: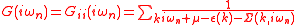
where
 denotes the lattice self-energy.
denotes the lattice self-energy.DMFT approximation: locality of the lattice self-energy
The only DMFT approximations (apart from the approximation that can be made in order to solve the Anderson model) consists in neglecting the spatial fluctuations of the lattice self-energySelf-energy
In theoretical physics and quantum field theory a particle's self-energy \Sigma represents the contribution to the particle's energy, or effective mass, due to interactions between the particle and the system it is part of...
, by equating it to the impurity self-energy:
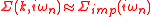
This approximation becomes exact in the limit of lattices with infinite coordination, that is when the number of neighbors of each site is infinite. Indeed, one can show that in the diagrammatic expansion of the lattice self-energy, only local diagrams survive when one goes into the infinite coordination limit.
Thus, as in classical mean-field theories, DMFT is supposed to get more accurate as the dimensionality (and thus the number of neighbors) increases. Other put, for low dimensions, spatial fluctuations will render the DMFT approximation less reliable.
The DMFT Loop
In order to find the local lattice Green's function, one has to determine the hybridization function such that the corresponding impurity Green's function will coincide with the sought-after local lattice Green's function. An intuitive method would be the following: for a given ,
,  and temperature
and temperature 
- First, compute the non-interacting lattice Green's function
 , and extract its local part
, and extract its local part 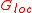
- The self-consistency condition requires it to be equal to the impurity Green's function,

- Compute the corresponding hybridization function through (1)
- Solve the AIM for a new impurity Green's function
 , extract its self-energy:
, extract its self-energy: 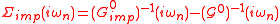
- Make the DMFT approximation:
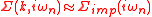
- Compute the new lattice Green's function, extract its local part and go back to step 2 with a new

Self-consistency is reached when
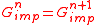 .
.Applications
The local lattice Green's function and other impurity observables can be used to calculate a number of physical quantities as a function of correlations , bandwidth, filling (chemical potential
, bandwidth, filling (chemical potential  ), and temperature
), and temperature  :
:
- the spectral function (which gives the band structure)
- the kinetic energyKinetic energyThe kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
- the double occupancy of a site
- response functions (compressibility, optical conductivity, specific heat)
In particular, the drop of the double-occupancy as
 increases is a signature of the Mott transition.
increases is a signature of the Mott transition.Extensions of DMFT
DMFT has several extensions, extending the above formalism to multi-orbital, multi-site problems.Multi-orbital extension
DMFT can be extended to Hubbard models with multiple orbitals, namely with electron-electron interactions of the form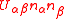 where
where  and
and  denote different orbitals. This is especially relevant for compounds whose
denote different orbitals. This is especially relevant for compounds whose  -orbitals are degenerate, such as iron in the newly discovered high-temperature iron-based superconductor
-orbitals are degenerate, such as iron in the newly discovered high-temperature iron-based superconductorIron-based superconductor
Iron-based superconductors are chemical compounds with superconducting properties. In 2008, led by recently discovered iron pnictide compounds , they were in the first stages of experimentation and implementation...
s (pnictides).
Cluster DMFT
In order to improve on the DMFT approximation, the Hubbard model can be mapped on a multi-site impurity (cluster) problem, which allows one to add some spatial dependence to the impurity self-energy. Typical clusters contain 4 to 8 sites.External links
- Strongly Correlated Materials: Insights From Dynamical Mean-Field Theory G. Kotliar and D. Vollhardt

