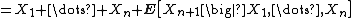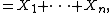Doob's martingale inequality
Encyclopedia
In mathematics
, Doob's martingale inequality is a result in the study of stochastic processes. It gives a bound on the probability that a stochastic process exceeds any given value over a given interval of time. As the name suggests, the result is usually given in the case that the process is a non-negative martingale
, but the result is also valid for non-negative submartingales.
The inequality is due to the American mathematician
Joseph Leo Doob
.
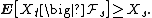
(For a continuous-time submartingale, assume further that the process is càdlàg.) Then, for any constant C > 0 and p ≥ 1,
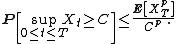
In the above, as is conventional, P denotes the probability measure
on the sample space Ω of the stochastic process
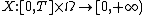
and E denotes the expected value
with respect to the probability measure P, i.e. the integral
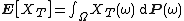
in the sense of Lebesgue integration
.
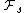denotes the σ-algebra generated by all the random variable
s Xi with i ≤ s; the collection of such σ-algebras forms a filtration
of the probability space.
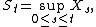
and for p ≥ 1 let
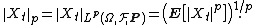
In this notation, Doob's inequality as stated above reads
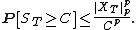
The following inequalities also hold: for p = 1,
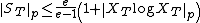
and, for p > 1,
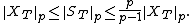
: if X1, X2, ... is a sequence of real-valued independent random variables, each with mean zero, it is clear that
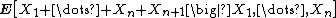
so Mn = X1 + ... + Xn is a martingale. Note that Jensen's inequality
implies that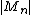
is a nonnegative submartingale if 
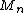is a martingale. Hence, taking p = 2 in Doob's martingale inequality,
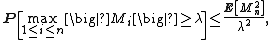
which is precisely the statement of Kolmogorov's inequality.
. Then
The proof is just as follows: since the exponential function is monotonically increasing, for any non-negative λ,
By Doob's inequality, and since the exponential of Brownian motion is a positive submartingale,
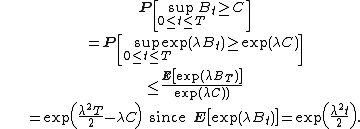
Since the left-hand side does not depend on λ, choose λ to minimize the right-hand side: λ = C / T gives the desired inequality.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Doob's martingale inequality is a result in the study of stochastic processes. It gives a bound on the probability that a stochastic process exceeds any given value over a given interval of time. As the name suggests, the result is usually given in the case that the process is a non-negative martingale
Martingale (probability theory)
In probability theory, a martingale is a model of a fair game where no knowledge of past events can help to predict future winnings. In particular, a martingale is a sequence of random variables for which, at a particular time in the realized sequence, the expectation of the next value in the...
, but the result is also valid for non-negative submartingales.
The inequality is due to the American mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Joseph Leo Doob
Joseph Leo Doob
Joseph Leo Doob was an American mathematician, specializing in analysis and probability theory.The theory of martingales was developed by Doob.-Early life and education:...
.
Statement of the inequality
Let X be a submartingale taking non-negative real values, either in discrete or continuous time. That is, for all times s and t with s < t,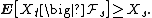(For a continuous-time submartingale, assume further that the process is càdlàg.) Then, for any constant C > 0 and p ≥ 1,
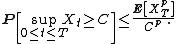
In the above, as is conventional, P denotes the probability measure
Probability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
on the sample space Ω of the stochastic process
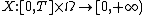
and E denotes the expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
with respect to the probability measure P, i.e. the integral
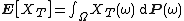
in the sense of Lebesgue integration
Lebesgue integration
In mathematics, Lebesgue integration, named after French mathematician Henri Lebesgue , refers to both the general theory of integration of a function with respect to a general measure, and to the specific case of integration of a function defined on a subset of the real line or a higher...
.
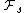denotes the σ-algebra generated by all the random variableRandom variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s Xi with i ≤ s; the collection of such σ-algebras forms a filtration
Filtration (abstract algebra)
In mathematics, a filtration is an indexed set Si of subobjects of a given algebraic structure S, with the index i running over some index set I that is a totally ordered set, subject to the condition that if i ≤ j in I then Si ⊆ Sj...
of the probability space.
Further inequalities
There are further (sub)martingale inequalities also due to Doob. With the same assumptions on X as above, let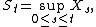and for p ≥ 1 let
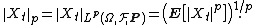
In this notation, Doob's inequality as stated above reads
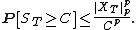
The following inequalities also hold: for p = 1,
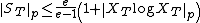
and, for p > 1,
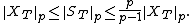
Related inequalities
Doob's inequality for discrete-time martingales implies Kolmogorov's inequalityKolmogorov's inequality
In probability theory, Kolmogorov's inequality is a so-called "maximal inequality" that gives a bound on the probability that the partial sums of a finite collection of independent random variables exceed some specified bound...
: if X1, X2, ... is a sequence of real-valued independent random variables, each with mean zero, it is clear that
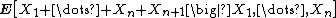
so Mn = X1 + ... + Xn is a martingale. Note that Jensen's inequality
Jensen's inequality
In mathematics, Jensen's inequality, named after the Danish mathematician Johan Jensen, relates the value of a convex function of an integral to the integral of the convex function. It was proved by Jensen in 1906. Given its generality, the inequality appears in many forms depending on the context,...
implies that
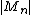is a nonnegative submartingale if 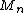is a martingale. Hence, taking p = 2 in Doob's martingale inequality,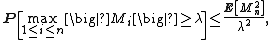which is precisely the statement of Kolmogorov's inequality.
Application: Brownian motion
Let B denote canonical one-dimensional Brownian motionBrownian motion
Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
. Then
The proof is just as follows: since the exponential function is monotonically increasing, for any non-negative λ,
By Doob's inequality, and since the exponential of Brownian motion is a positive submartingale,
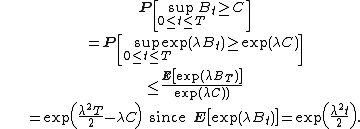
Since the left-hand side does not depend on λ, choose λ to minimize the right-hand side: λ = C / T gives the desired inequality.