Dialectica interpretation
Encyclopedia
In proof theory
, the Dialectica interpretation
is a proof interpretation of intuitionistic arithmetic (Heyting arithmetic
) into a finite type extension of primitive recursive arithmetic
, the so-called System T. It was developed by Kurt Gödel
to provide a consistency proof
of arithmetic. The name of the interpretation comes from the journal Dialectica
, where Gödel's paper was published in a special issue dedicated to Paul Bernays
on his 70th birthday.
, the consistency of classical Peano arithmetic had already been reduced to the consistency of intuitionistic Heyting arithmetic
. Gödel's motivation for developing the dialectica interpretation was to obtain a relative consistency
proof for Heyting arithmetic (and hence for Peano arithmetic).
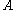of Heyting arithmetic is mapped to a quantifier-free formula 
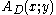of the system T, where 
and 
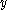are tuples of fresh variables (not appearing free in 
). Intuitively, 
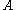is interpreted as 
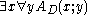. The proof translation shows how a proof of 
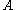has enough information to witness the interpretation of 
, i.e. the proof of 
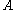can be converted into a closed term 
and a proof of 
in the system T.
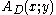is defined inductively on the logical structure of 
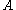as follows, where 
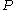is an atomic formula:
Proof theory
Proof theory is a branch of mathematical logic that represents proofs as formal mathematical objects, facilitating their analysis by mathematical techniques. Proofs are typically presented as inductively-defined data structures such as plain lists, boxed lists, or trees, which are constructed...
, the Dialectica interpretation
is a proof interpretation of intuitionistic arithmetic (Heyting arithmetic
Heyting arithmetic
In mathematical logic, Heyting arithmetic is an axiomatization of arithmetic in accordance with the philosophy of intuitionism. It is named after Arend Heyting, who first proposed it....
) into a finite type extension of primitive recursive arithmetic
Primitive recursive arithmetic
Primitive recursive arithmetic, or PRA, is a quantifier-free formalization of the natural numbers. It was first proposed by Skolem as a formalization of his finitist conception of the foundations of arithmetic, and it is widely agreed that all reasoning of PRA is finitist...
, the so-called System T. It was developed by Kurt Gödel
Kurt Gödel
Kurt Friedrich Gödel was an Austrian logician, mathematician and philosopher. Later in his life he emigrated to the United States to escape the effects of World War II. One of the most significant logicians of all time, Gödel made an immense impact upon scientific and philosophical thinking in the...
to provide a consistency proof
Consistency proof
In logic, a consistent theory is one that does not contain a contradiction. The lack of contradiction can be defined in either semantic or syntactic terms. The semantic definition states that a theory is consistent if and only if it has a model, i.e. there exists an interpretation under which all...
of arithmetic. The name of the interpretation comes from the journal Dialectica
Dialectica
Dialectica is a quarterly philosophy journal published by Blackwell. The journal was founded in 1947 by Gaston Bachelard, Paul Bernays and Ferdinand Gonseth. Dialectica is edited in Switzerland and has a focus on analytical philosophy. The journal is the official journal of the European...
, where Gödel's paper was published in a special issue dedicated to Paul Bernays
Paul Bernays
Paul Isaac Bernays was a Swiss mathematician, who made significant contributions to mathematical logic, axiomatic set theory, and the philosophy of mathematics. He was an assistant to, and close collaborator of, David Hilbert.-Biography:Bernays spent his childhood in Berlin. Bernays attended the...
on his 70th birthday.
Motivation
Via the Gödel–Gentzen negative translationGödel–Gentzen negative translation
In proof theory, the Gödel–Gentzen negative translation is a method for embedding classical first-order logic into intuitionistic first-order logic. It is one of a number of double-negation translations that are of importance to the metatheory of intuitionistic logic...
, the consistency of classical Peano arithmetic had already been reduced to the consistency of intuitionistic Heyting arithmetic
Heyting arithmetic
In mathematical logic, Heyting arithmetic is an axiomatization of arithmetic in accordance with the philosophy of intuitionism. It is named after Arend Heyting, who first proposed it....
. Gödel's motivation for developing the dialectica interpretation was to obtain a relative consistency
Consistency
Consistency can refer to:* Consistency , the psychological need to be consistent with prior acts and statements* "Consistency", an 1887 speech by Mark Twain...
proof for Heyting arithmetic (and hence for Peano arithmetic).
Dialectica interpretation of intuitionistic logic
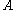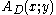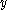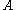The interpretation has two components: a formula translation and a proof translation. The formula translation describes how each formula of Heyting arithmetic is mapped to a quantifier-free formula of the system T, where and are tuples of fresh variables (not appearing free in ). Intuitively, is interpreted as 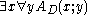. The proof translation shows how a proof of 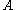has enough information to witness the interpretation of , i.e. 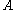the proof of can be converted into a closed term and a proof of in the system T.Formula translation
The quantifier-free formula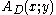 is defined inductively on the logical structure of 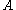as follows, where 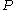is an atomic formula:-
Proof translation (soundness)
The formula interpretation is such that whenever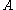
is provable in Heyting arithmetic then there exists a sequence of closed terms 
such that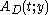 
is provable in the system T. The sequence of terms 
and the proof of 
are constructed from the given proof of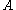 
in Heyting arithmetic. The construction of 
is quite straightforward, except for the contraction axiom 
which requires the assumption that quantifier-free formulas are decidable.
Characterisation principles
It has also been shown that Heyting arithmetic extended with the following principles
- Axiom of choice
- Markov's principleMarkov's principleMarkov's principle, named after Andrey Markov Jr, is a classical tautology that is not intuitionistically valid but that may be justified by constructive means.There are many equivalent formulations of Markov's principle.- Statements of the principle :...
- Independence of premiseIndependence of premiseIn proof theory and constructive mathematics, the principle of independence of premise states that if φ and ∃ x θ are sentences in a formal theory and is provable, then is provable. Here x cannot be a free variable of φ....
for universal formulas
is necessary and sufficient for characterising the formulas of HA which are interpretable by the Dialectica interpretation.
Extensions of basic interpretation
The basic dialectica interpretation of intuitionistic logic has been extended to various stronger systems. Intuitively, the dialectica interpretation can be applied to a stronger system, as long as the dialectica interpretation of the extra principle can be witnessed by terms in the system T (or an extension of system T).
Induction
Given Gödel's incompleteness theorem (which implies that the consistency of PA cannot be proven by finitisticFinitismIn the philosophy of mathematics, one of the varieties of finitism is an extreme form of constructivism, according to which a mathematical object does not exist unless it can be constructed from natural numbers in a finite number of steps...
means) it is reasonable to expect that system T must contain non-finitistic constructions. Indeed this is the case. The non-finitistic constructions show up in the interpretation of mathematical inductionMathematical inductionMathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
. To give a Dialectica interpretation of induction, Gödel makes use of what is nowadays called Gödel's primitive recursive functionalPrimitive recursive functionalIn mathematical logic, the primitive recursive functionals are a generalization of primitive recursive functions into higher type theory. They consist of a collection of functions in all pure finite types....
s, which are higher order functions with primitive recursive descriptions.
Classical logic
Formulas and proofs in classical arithmetic can also be given a dialectica interpretation via an initial embedding into Heyting arithmetic followed the dialectica interpretation of Heyting arithmetic. Shoenfield, in his book, combines the negative translation and the dialectica interpretation into a single interpretation of classical arithmetic.
Comprehension
In 1962 Spector
extended Gödel's Dialectica interpretation of arithmetic to full mathematical analysis, by showing how the schema of countable choice can be given a Dialectica interpretation by extending system T with bar recursionBar recursionBar recursion is a generalized form of recursion developed by Spector in his 1962 paper . It is related to bar induction in the same fashion that primitive recursion is related to ordinary induction, or transfinite recursion is related to transfinite induction....
.
Dialectica interpretation of linear logic
The Dialectica interpretation has been used to build a model of Girard's refinement of intuitionistic logicIntuitionistic logicIntuitionistic logic, or constructive logic, is a symbolic logic system differing from classical logic in its definition of the meaning of a statement being true. In classical logic, all well-formed statements are assumed to be either true or false, even if we do not have a proof of either...
known as linear logicLinear logicLinear logic is a substructural logic proposed by Jean-Yves Girard as a refinement of classical and intuitionistic logic, joining the dualities of the former with many of the constructive properties of the latter...
, via the so-called Dialectica spaces. Since linear logic is a refinement of intuitionistic logic, the dialectica interpretation of linear logic can also be viewed as a refinement of the dialectica interpretation of intuitionistic logic.
Although the linear interpretation in validates the weakening rule (it is actually an interpretation of affine logicAffine logicAffine logic is a substructural logic whose proof theory rejects the structural rule of contraction. It can also be characterized as linear logic with weakening....
), the dialectica spaces interpretation does not validate weakening for arbitrary formulas.
Variants of the dialectica interpretation
Several variants of the Dialectica interpretation have been proposed since. Most notably the Diller-Nahm variant (to avoid the contraction problem) and Kohlenbach's monotone and Ferreira-Oliva bounded interpretations (to interpret weak König's lemma).
Comprehensive treatments of the interpretation can be found at
,
and
.