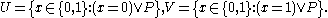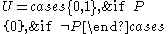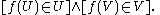Diaconescu's theorem
Encyclopedia
In mathematical logic
, Diaconescu's theorem
, or the Goodman–Myhill theorem, states that the full axiom of choice is sufficient to derive the law of the excluded middle, or restricted forms of it, in constructive set theory
. It was discovered in 1975 by Diaconescu and later by Goodman and Myhill.
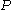 , we can build the sets
, we can build the sets
These are sets, using the axiom of specification. In classical set theory this would be equivalent to
and similarly for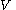 . However, without the law of the excluded middle, these equivalences cannot be proven; in fact the two sets are not even provably finite (in the usual sense of being in bijection
. However, without the law of the excluded middle, these equivalences cannot be proven; in fact the two sets are not even provably finite (in the usual sense of being in bijection
with a natural number
, though they would be in the Dedekind sense).
By the axiom of choice, there will exist a choice function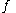 for the set
for the set 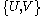 ; that is, a function
; that is, a function 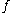 such that
such that
By the definition of the two sets, this means that
which implies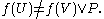
But since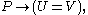 (by the axiom of extensionality
(by the axiom of extensionality
),
therefore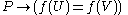 ,
,
so
Thus As this could be done for any proposition, this completes the proof that the axiom of choice implies the law of the excluded middle.
As this could be done for any proposition, this completes the proof that the axiom of choice implies the law of the excluded middle.
The proof relies on the use of the full separation axiom. In constructive set theory usually only predicative separation
is permitted. Thus the form of P will be restricted to sentences with bound quantifiers only, giving only a restricted form of the law of the excluded middle. This restricted form is still not acceptable constructively.
In constructive type theory, or in Heyting arithmetic
extended with finite types, there is typically no separation at all - subsets of a type are given different treatments. A form of the axiom of choice is a theorem, yet excluded middle is not.
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
, Diaconescu's theorem
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
, or the Goodman–Myhill theorem, states that the full axiom of choice is sufficient to derive the law of the excluded middle, or restricted forms of it, in constructive set theory
Constructive set theory
Constructive set theory is an approach to mathematical constructivism following the program of axiomatic set theory. That is, it uses the usual first-order language of classical set theory, and although of course the logic is constructive, there is no explicit use of constructive types...
. It was discovered in 1975 by Diaconescu and later by Goodman and Myhill.
Proof
For any proposition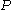 , we can build the sets
, we can build the setsSet-builder notation
In set theory and its applications to logic, mathematics, and computer science, set-builder notation is a mathematical notation for describing a set by stating the properties that its members must satisfy...
These are sets, using the axiom of specification. In classical set theory this would be equivalent to
and similarly for
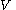 . However, without the law of the excluded middle, these equivalences cannot be proven; in fact the two sets are not even provably finite (in the usual sense of being in bijection
. However, without the law of the excluded middle, these equivalences cannot be proven; in fact the two sets are not even provably finite (in the usual sense of being in bijectionBijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
with a natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
, though they would be in the Dedekind sense).
By the axiom of choice, there will exist a choice function
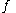 for the set
for the set 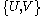 ; that is, a function
; that is, a function 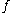 such that
such thatBy the definition of the two sets, this means that
-
 ,
,
which implies
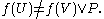
But since
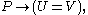 (by the axiom of extensionality
(by the axiom of extensionalityAxiom of extensionality
In axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of extensionality, or axiom of extension, is one of the axioms of Zermelo-Fraenkel set theory.- Formal statement :...
),
therefore
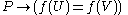 ,
,so

Thus
 As this could be done for any proposition, this completes the proof that the axiom of choice implies the law of the excluded middle.
As this could be done for any proposition, this completes the proof that the axiom of choice implies the law of the excluded middle.The proof relies on the use of the full separation axiom. In constructive set theory usually only predicative separation
Axiom schema of predicative separation
In axiomatic set theory, the axiom schema of predicative separation, or of restricted, or Δ0 separation, is a schema of axioms which is a restriction of the usual axiom schema of separation in Zermelo-Fraenkel set theory. It only asserts the existence of a subset of a set if that subset can...
is permitted. Thus the form of P will be restricted to sentences with bound quantifiers only, giving only a restricted form of the law of the excluded middle. This restricted form is still not acceptable constructively.
In constructive type theory, or in Heyting arithmetic
Heyting arithmetic
In mathematical logic, Heyting arithmetic is an axiomatization of arithmetic in accordance with the philosophy of intuitionism. It is named after Arend Heyting, who first proposed it....
extended with finite types, there is typically no separation at all - subsets of a type are given different treatments. A form of the axiom of choice is a theorem, yet excluded middle is not.