
Dense submodule
Encyclopedia
In abstract algebra
, specifically in module theory, a dense submodule of a module is a refinement of the notion of an essential submodule. If N is a dense submodule of M, it may also be said it may alternatively be said that "N ⊆ M is a rational extension". Dense submodules are connected with rings of quotients in noncommutative ring theory. Most of the results appearing here were first established in , and .
It should be noticed that this terminology is different from the notion of a dense subset in general topology
. No topology is needed to define a dense submodule, and a dense submodule may or may not be topologically dense in a module with topology.
appearing in and . Let R be a ring, and M be a right R module with submodule N. For an element y of M, define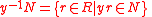
Note that the expression y−1 is only formal and that y is not necessarily invertible, but it helps to suggest that y⋅(y−1N) ⊆ N. The set y −1N is always a right ideal
of R.
A submodule N of M is said to be a dense submodule if for all x and y in M with x ≠ 0, there exists an r in R such that xr ≠ {0} and yr is in N. In other words, using the introduced notation, the set
In this case, the relationship is denoted by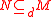
Another equivalent definition is homological
in nature: N is dense in M if and only if
where E(M) is the injective hull
of M.
. The analogous construction using a maximal dense extension results in the rational hull Ẽ(M) which is a submodule of E(M). When a module has no proper rational extension, so that Ẽ(M) = M, the module is said to be rationally complete. If R is right nonsingular, then of course Ẽ(M) = E(M).
The rational hull is readily identified within the injective hull. Let S=EndR(E(M)) be the endomorphism ring
of the injective hull. Then an element x of the injective hull is in the rational hull if and only if x is sent to zero by all maps in S which are zero on M. In symbols,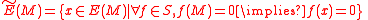
In general, there may be maps in S which are zero on M and yet are nonzero for some x not in M, and such an x would not be in the rational hull.
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, specifically in module theory, a dense submodule of a module is a refinement of the notion of an essential submodule. If N is a dense submodule of M, it may also be said it may alternatively be said that "N ⊆ M is a rational extension". Dense submodules are connected with rings of quotients in noncommutative ring theory. Most of the results appearing here were first established in , and .
It should be noticed that this terminology is different from the notion of a dense subset in general topology
General topology
In mathematics, general topology or point-set topology is the branch of topology which studies properties of topological spaces and structures defined on them...
. No topology is needed to define a dense submodule, and a dense submodule may or may not be topologically dense in a module with topology.
Definition
This article modifies expositionExposition (literary technique)
At the beginning of a narrative, the exposition is the author's providing of some background information to the audience about the plot, characters' histories, setting, and theme. Exposition is considered one of four rhetorical modes of discourse, along with argumentation, description, and narration...
appearing in and . Let R be a ring, and M be a right R module with submodule N. For an element y of M, define
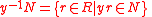
Note that the expression y−1 is only formal and that y is not necessarily invertible, but it helps to suggest that y⋅(y−1N) ⊆ N. The set y −1N is always a right ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
of R.
A submodule N of M is said to be a dense submodule if for all x and y in M with x ≠ 0, there exists an r in R such that xr ≠ {0} and yr is in N. In other words, using the introduced notation, the set

In this case, the relationship is denoted by
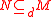
Another equivalent definition is homological
Homological algebra
Homological algebra is the branch of mathematics which studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and...
in nature: N is dense in M if and only if

where E(M) is the injective hull
Injective hull
In mathematics, especially in the area of abstract algebra known as module theory, the injective hull of a module is both the smallest injective module containing it and the largest essential extension of it...
of M.
Properties
- It can be shown that N is an essential submodule of M if and only if for all y ≠ 0 in M, the set y⋅(y −1N) ≠ {0}. Clearly then, every dense submodule is an essential submodule.
- If M is a nonsingular module, then N is dense in M if and only if it is essential in M.
- A ring is a right nonsingular ring if and only if its essential right ideals are all dense right ideals.
- If N and N' are dense submodules of M, then so is N ∩ N' .
- If N is dense and N ⊆ K ⊆ M, then K is also dense.
- If B is a dense right ideal in R, then so is y−1B for any y in R.
Examples
- If x is a non-zerodivisor in the centerCenter (algebra)The term center or centre is used in various contexts in abstract algebra to denote the set of all those elements that commute with all other elements. It is often denoted Z, from German Zentrum, meaning "center". More specifically:...
of R, then xR is a dense right ideal of R. - If I is a two-sided ideal of R, I is dense as a right ideal if and only if the left annihilatorAnnihilatorAnnihilator may refer to:* Annihilator , a mathematical concept* The annihilator of a vector subspace* Annihilator method, a type of differential operator, used in a particular method for solving differential equations...
of I is zero, that is, . In particular in commutative rings, the dense ideals are precisely the ideals which are faithful modules.
. In particular in commutative rings, the dense ideals are precisely the ideals which are faithful modules.
Rational hull of a module
Every right R module M has a maximal essential extension E(M) which is its injective hullInjective hull
In mathematics, especially in the area of abstract algebra known as module theory, the injective hull of a module is both the smallest injective module containing it and the largest essential extension of it...
. The analogous construction using a maximal dense extension results in the rational hull Ẽ(M) which is a submodule of E(M). When a module has no proper rational extension, so that Ẽ(M) = M, the module is said to be rationally complete. If R is right nonsingular, then of course Ẽ(M) = E(M).
The rational hull is readily identified within the injective hull. Let S=EndR(E(M)) be the endomorphism ring
Endomorphism ring
In abstract algebra, one associates to certain objects a ring, the object's endomorphism ring, which encodes several internal properties of the object; this may be denoted End...
of the injective hull. Then an element x of the injective hull is in the rational hull if and only if x is sent to zero by all maps in S which are zero on M. In symbols,
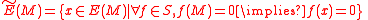
In general, there may be maps in S which are zero on M and yet are nonzero for some x not in M, and such an x would not be in the rational hull.
Maximal right ring of quotients
The maximal right ring of quotients can be described in two ways in connection with dense right ideals of R.- In one method, Ẽ(R) is shown to be module isomorphic to a certain endomorphism ring, and the ring structure is taken across this isomorphism to imbue Ẽ(R) with a ring structure, that of the maximal right ring of quotients.
- In a second method, the maximal right ring of quotients is identified with a set of equivalence classes of homomorphisms from dense right ideals of R into R. The equivalence relation says that two functions are equivalent if they agree on a dense right ideal of R.

