Kakuro or Kakkuro is a kind of logic puzzle

Logic puzzle

A logic puzzle is a puzzle deriving from the mathematics field of deduction.-History:The logic puzzle was first produced by Charles Lutwidge Dodgson, who is better known under his pen name Lewis Carroll, the author of Alice's Adventures in Wonderland...

 that is often referred to as a mathematical

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

 transliteration

Transliteration

Transliteration is a subset of the science of hermeneutics. It is a form of translation, and is the practice of converting a text from one script into another...

 of the crossword

Crossword

A crossword is a word puzzle that normally takes the form of a square or rectangular grid of white and shaded squares. The goal is to fill the white squares with letters, forming words or phrases, by solving clues which lead to the answers. In languages that are written left-to-right, the answer...

. Kakuro puzzles are regular features in many math-and-logic puzzle publications in the United States. Dell Magazines

Dell Magazines

Dell Magazines was a company founded by George T. Delacorte Jr. in 1921 as part of his Dell Publishing Co. Dell is today known for its many puzzle magazines, as well as fiction magazines such as Alfred Hitchcock's Mystery Magazine, Ellery Queen's Mystery Magazine, Asimov's Science Fiction, and...

 came up with the original English name Cross Sums and other names such as Cross Addition have also been used, but the Japanese name Kakuro, abbreviation of Japanese kasan kurosu, (加算クロス, addition cross) seems to have gained general acceptance and the puzzles appear to be titled this way now in most publications. The popularity of Kakuro in Japan is immense, second only to Sudoku

Sudoku

is a logic-based, combinatorial number-placement puzzle. The objective is to fill a 9×9 grid with digits so that each column, each row, and each of the nine 3×3 sub-grids that compose the grid contains all of the digits from 1 to 9...

 among Nikoli

Nikoli

Nikoli Co., Ltd. is a Japanese publisher that specializes in games and, especially, logic puzzles. Nikoli is also the nickname of a quarterly magazine issued by the company...

's famed logic-puzzle offerings.http://www.conceptispuzzles.com/index.aspx?uri=puzzle/kakuro/history

The canonical

Canonical

Canonical is an adjective derived from canon. Canon comes from the greek word κανών kanon, "rule" or "measuring stick" , and is used in various meanings....

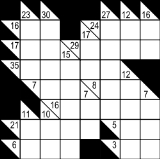
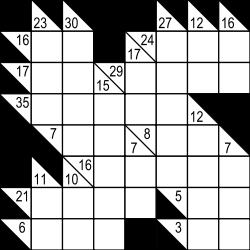
 Kakuro puzzle is played in a grid of filled and barred cells, "black" and "white" respectively. Puzzles are usually 16×16 in size, although these dimensions can vary widely. Apart from the top row and leftmost column which are entirely black, the grid is divided into "entries" — lines of white cells — by the black cells. The black cells contain a diagonal slash from upper-left to lower-right and a number in one or both halves, such that each horizontal entry has a number in the black half-cell to its immediate left and each vertical entry has a number in the black half-cell immediately above it. These numbers, borrowing crossword terminology, are commonly called "clues".

The object of the puzzle is to insert a digit from 1 to 9 inclusive into each white cell such that the sum of the numbers in each entry matches the clue associated with it and that no digit is duplicated in any entry. It is that lack of duplication that makes creating Kakuro puzzles with unique solutions possible, and which means solving a Kakuro puzzle involves investigating combination

Combination

In mathematics a combination is a way of selecting several things out of a larger group, where order does not matter. In smaller cases it is possible to count the number of combinations...

s more, compared to Sudoku in which the focus is on permutation

Permutation

In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...

s. There is an unwritten rule for making Kakuro puzzles that each clue must have at least two numbers that add up to it. This is because including one number is mathematically trivial when solving Kakuro puzzles; one can simply disregard the number entirely and subtract it from the clue it indicates.

At least one publisher includes the constraint that a given combination of numbers can only be used once in each grid, but still markets the puzzles as plain Kakuro.

Some publishers prefer to print their Kakuro grids exactly like crossword grids, with no labeling in the black cells and instead numbering the entries, providing a separate list of the clues akin to a list of crossword clues. (This eliminates the row and column that are entirely black.) This is purely an issue of image and does not affect solving.

In discussing Kakuro puzzles and tactics, the typical shorthand for referring to an entry is "(clue, in numerals)-in-(number of cells in entry, spelled out)", such as "16-in-two" and "25-in-five". The exception is what would otherwise be called the "45-in-nine" — simply "45" is used, since the "-in-nine" is mathematically implied (nine cells is the longest possible entry, and since it cannot duplicate a digit it must consist of all the digits from 1 to 9 once). Curiously, "3-in-two", "4-in-two", "43-in-eight", and "44-in-eight" are still frequently called as such, despite the "-in-two" and "-in-eight" being equally implied.

Solving techniques

Although brute-force guessing is of course possible, a better weapon is the understanding of the various combinatorial forms that entries can take for various pairings of clues and entry lengths. Those entries with sufficiently large or small clues for their length will have fewer possible combinations to consider, and by comparing them with entries that cross them, the proper permutation — or part of it — can be derived. The simplest example is where a 3-in-two crosses a 4-in-two: the 3-in-two must consist of '1' and '2' in some order; the 4-in-two (since '2' cannot be duplicated) must consist of '1' and '3' in some order. Therefore, their intersection must be '1', the only digit they have in common.

When solving longer sums there are additional ways to find clues to locating the correct digits. One such method would be to note where a few squares together share possible values thereby eliminating the possibility that other squares in that sum could have those values. For instance, if two 4-in-two clues cross with a longer sum, then the 1 and 3 in the solution must be in those two squares and those digits cannot be used elsewhere in that sum.

When solving sums which have a limited number of solution sets then that can lead to useful clues. For instance, a 30-in-seven sum only has two solution sets: {1,2,3,4,5,6,9} and {1,2,3,4,5,7,8}. If one of the squares in that sum can only take on the values of {8,9} (if the crossing clue is a 17-in-two sum, for example) then that not only becomes an indicator of which solution set fits this sum, it eliminates the possibility of any other digit in the sum being either of those two values, even before determining which of the two values fits in that square.

Another useful approach in more complex puzzles is to identify which square a digit goes in by eliminating other locations within the sum. If all of the crossing clues of a sum have many possible values, but it can be determined that there is only one square which could have a particular value which the sum in question must have, then whatever other possible values the crossing sum would allow, that intersection must be the isolated value. For example, a 36-in-eight sum must contain all digits except 9. If only one of the squares could take on the value of 2 then that must be the answer for that square.

A "box technique" can also be applied on occasion, when the geometry of the unfilled white cells at any given stage of solving lends itself to it: by summing the clues for a series of horizontal entries (subtracting out the values of any digits already added to those entries) and subtracting the clues for a mostly-overlapping series of vertical entries, the difference can reveal the value of a partial entry, often a single cell. This is possible due to the fact that addition is both associative and commutative.

It is common practice to mark potential values for cells in the cell corners until all but one have been proven impossible; for particularly challenging puzzles, sometimes entire ranges of values for cells are noted by solvers in the hope of eventually finding sufficient constraints to those ranges from crossing entries to be able to narrow the ranges to single values. Because of space constraints, instead of digits some solvers use a positional notation, where a potential numerical value is represented by a mark in a particular part of the cell, which makes it easy to place several potential values into a single cell. This also makes it easier to distinguish potential values from solution values.

Some solvers also use graph paper

Graph paper

Graph paper, graphing paper, grid paper or millimeter paper is writing paper that is printed with fine lines making up a regular grid. The lines are often used as guides for plotting mathematical functions or experimental data and drawing diagrams. It is commonly found in mathematics and...

 to try various digit combinations before writing them into the puzzle grids.

Mathematics of Kakuro

Kakuro puzzles are NP-complete

NP-complete

In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...

There are two kinds of mathematical symmetry readily identifiable in kakuro puzzles: minimum and maximum constraints are duals, as are missing and required values.

All sum combinations can be represented using a bitmapped representation. This representation is useful for determining missing and required values using bitwise logic operations

Bitwise operation

A bitwise operation operates on one or more bit patterns or binary numerals at the level of their individual bits. This is used directly at the digital hardware level as well as in microcode, machine code and certain kinds of high level languages...

.

Variants

A relatively common variant of Kakuro is its logical successor, Cross Products (or Cross Multiplication), where the clues are the product of the digits in the entries rather than the sum. Dell Magazines has produced such puzzles, but also allowed repeating of digits aside from 1 due to space limitations in the number of digits in each product in a puzzle. On the other hand, puzzles by Games Magazines are more like crossword puzzles, allowing the implementation of the no-repeating digits rule.

Another variant is having a different range of values that are inserted in the cells, such as 1 to 12, instead of the standard 1 to 9.

A genuine combination of Sudoku and Kakuro is the so called "Cross Sums Sudoku" in which clues
are given as cross sums on a standard 9 x 9 Sudoku grid. A relevant variant is the so-called "Cryptic Kakuro"
where the clues are given in terms of alphametics and each number represents a digit from 1 to 9.

The final puzzle of the 2004 United States qualifier for the World Puzzle Championship

World Puzzle Championship

The World Puzzle Championship is an annual international puzzle competition run by the World Puzzle Federation. The first one was held in New York in 1992...

 is titled Cross Number Sums Place: it is a Cross Sums where every row and column of the grid (except the top row and leftmost column as usual) contains exactly nine white cells, none of which — even across multiple entries — are allowed to use the same digit twice, like a Number Place (Sudoku

Sudoku

is a logic-based, combinatorial number-placement puzzle. The objective is to fill a 9×9 grid with digits so that each column, each row, and each of the nine 3×3 sub-grids that compose the grid contains all of the digits from 1 to 9...

); in addition, small circles are printed on the borders between some white cells; numerically adjacent digits must be placed astride those circles, and may not appear orthogonally adjacent when not astride a circle.

External links

• Tutorial at Nikoli (Macromedia Flash required)
• The New Grid on the Block: The Guardian
  The Guardian
  The Guardian, formerly known as The Manchester Guardian , is a British national daily newspaper in the Berliner format...
  
  newspaper's introduction to Kakuro
• Table of combinations for use in Kakuro
• Kakuro Combinations Helper App
• Kakuro Tutorial - Basic
• Kakuro Tutorial - Advanced