
Corner transfer matrix
Encyclopedia
In statistical mechanics
, the corner transfer matrix describes the effect of adding a quadrant to a lattice. Introduced by Rodney Baxter in 1968 as an extension of the Kramers-Wannier row-to-row transfer matrix, it provides a powerful method of studying lattice models. Calculations with corner transfer matrices led Baxter to the exact solution of the hard hexagon model
in 1980.
σi assigned to each site i and interactions limited to spins around a common face. Let the total energy be given by

where for each face the surrounding sites i, j, k and l are arranged as follows:
For a lattice with N sites, the partition function
is

where the sum is over all possible spin configurations and w is the Boltzmann weight

To simplify the notation, we use a ferromagnetic Ising-type lattice
where each spin has the value +1 or −1, and the ground state is given by all spins up (i.e. the total energy is minimised when all spins on the lattice have the value +1). We also assume the lattice has 4-fold rotational symmetry (up to boundary conditions) and is reflection-invariant. These simplifying assumptions are not crucial, and extending the definition to the general case is relatively straightforward.
Now consider the lattice quadrant shown below:
The outer boundary sites, marked by triangles, are assigned their ground state spins (+1 in this case). The sites marked by open circles form the inner boundaries of the quadrant; their associated spin sets are labelled {σ1,…,σm} and {σ'1,…,σ'm}, where σ1 = σ'1. There are 2m possible configurations for each inner boundary, so we define a 2m×2m matrix entry-wise by

The matrix A, then, is the corner transfer matrix for the given lattice quadrant. Since the outer boundary spins are fixed and the sum is over all interior spins, each entry of A is a function of the inner boundary spins. The Kronecker delta in the expression ensures that σ1 = σ'1, so by ordering the configurations appropriately we may cast A as a block diagonal matrix:

Corner transfer matrices are related to the partition function in a simple way. In our simplified example, we construct the full lattice from four rotated copies of the lattice quadrant, where the inner boundary spin sets σ, σ', σ" and σ'" are allowed to differ:
The partition function is then written in terms of the corner transfer matrix A as
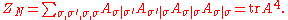
Like their row-to-row counterparts, corner transfer matrices may be factored into face transfer matrices, which correspond to adding a single face to the lattice. For the lattice quadrant given earlier, the face transfer matrices are of size 2m×2m and defined entry-wise by
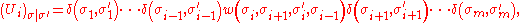
where 2 ≤ i ≤ m+1. Near the outer boundary, specifically, we have
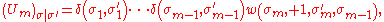

So the corner transfer matrix A factorises as

where

Graphically, this corresponds to:
We also require the 2m×2m matrices A* and A**, defined entry-wise by
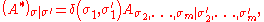
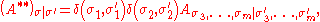
where the A matrices whose entries appear on the RHS are of size 2m-1×2m-1 and 2m-2×2m-2 respectively. This is more clearly written as
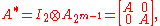

Now from the definitions of A, A*, A**, Ui and Fj, we have

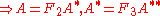

which gives the recursion relation for A2m in terms of A2m-1 and A2m-2.
Recalling that the lattice in our example is reflection-invariant, in the sense that
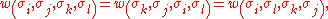
we see that A is a symmetric matrix (i.e. it is diagonalisable by an orthogonal matrix). So we write

where Ad is a diagonal matrix (normalised such that its numerically largest entry is 1), αm is the largest eigenvalue of A, and PTP = I. Likewise for A* and A**, we have

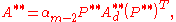
where Ad*, Ad**, P* and P** are defined in an analogous fashion to A* and A**, i.e. in terms of the smaller (normalised) diagonal forms and (orthogonal) eigenvector matrices of A2m-1 and A2m-2.
By substituting these diagonalisations into the recursion relation, we obtain

where
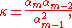

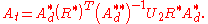
Now At is also symmetric, and may be calculated if Ad*, Ad** and R* are known; diagonalising At then yields its normalised diagonal form Ad, its largest eigenvalue κ, and its orthogonal eigenvector matrix R.
at a particular site deep inside the lattice. For the full lattice given earlier, the spin expectation value at the central site is given by

With the configurations ordered such that A is block diagonal as before, we may define a 2m×2m diagonal matrix
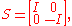
such that
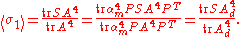
and written as

In our example, this reduces to

since tr Ad4 is a convergent sum as m → ∞ and Ad becomes infinite-dimensional. Furthermore, the number of faces 2m(m+1) approaches the number of sites N in the thermodynamic limit, so we have

which is consistent with the earlier equation giving κ as the largest eigenvalue for At. In other words, the partition function per site is given exactly by the diagonalised recursion relation for corner transfer matrices in the thermodynamic limit; this allows κ to be approximated via the iterative process of calculating Ad for a large lattice.
The matrices involved grow exponentially in size, however, and in actual numerical calculations they must be truncated at each step. One way of doing this is to keep the n largest eigenvalues at each step, for some fixed n. In most cases, the sequence of approximations obtained by taking n = 1,2,3,… converges rapidly, and to the exact value (for an exactly solvable model).
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
, the corner transfer matrix describes the effect of adding a quadrant to a lattice. Introduced by Rodney Baxter in 1968 as an extension of the Kramers-Wannier row-to-row transfer matrix, it provides a powerful method of studying lattice models. Calculations with corner transfer matrices led Baxter to the exact solution of the hard hexagon model
Hard hexagon model
In statistical mechanics, the hard hexagon model is a 2-dimensional lattice model of a gas, where particles are allowed to be on the vertices of a triangular lattice but no two particles may be adjacent....
in 1980.
Definition
Consider an IRF (interaction-round-a-face) model, i.e. a square lattice model with a spinSpin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
σi assigned to each site i and interactions limited to spins around a common face. Let the total energy be given by

where for each face the surrounding sites i, j, k and l are arranged as follows:
For a lattice with N sites, the partition function
Partition function (statistical mechanics)
Partition functions describe the statistical properties of a system in thermodynamic equilibrium. It is a function of temperature and other parameters, such as the volume enclosing a gas...
is

where the sum is over all possible spin configurations and w is the Boltzmann weight

To simplify the notation, we use a ferromagnetic Ising-type lattice
Ising model
The Ising model is a mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables called spins that can be in one of two states . The spins are arranged in a graph , and each spin interacts with its nearest neighbors...
where each spin has the value +1 or −1, and the ground state is given by all spins up (i.e. the total energy is minimised when all spins on the lattice have the value +1). We also assume the lattice has 4-fold rotational symmetry (up to boundary conditions) and is reflection-invariant. These simplifying assumptions are not crucial, and extending the definition to the general case is relatively straightforward.
Now consider the lattice quadrant shown below:
The outer boundary sites, marked by triangles, are assigned their ground state spins (+1 in this case). The sites marked by open circles form the inner boundaries of the quadrant; their associated spin sets are labelled {σ1,…,σm} and {σ'1,…,σ'm}, where σ1 = σ'1. There are 2m possible configurations for each inner boundary, so we define a 2m×2m matrix entry-wise by

The matrix A, then, is the corner transfer matrix for the given lattice quadrant. Since the outer boundary spins are fixed and the sum is over all interior spins, each entry of A is a function of the inner boundary spins. The Kronecker delta in the expression ensures that σ1 = σ'1, so by ordering the configurations appropriately we may cast A as a block diagonal matrix:

Corner transfer matrices are related to the partition function in a simple way. In our simplified example, we construct the full lattice from four rotated copies of the lattice quadrant, where the inner boundary spin sets σ, σ', σ" and σ'" are allowed to differ:
The partition function is then written in terms of the corner transfer matrix A as
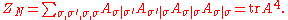
Recursion relation
A corner transfer matrix A2m (defined for an m×m quadrant) may be expressed in terms of smaller corner transfer matrices A2m-1 and A2m-2 (defined for reduced (m-1)×(m-1) and (m-2)×(m-2) quadrants respectively). This recursion relation allows, in principle, the iterative calculation of the corner transfer matrix for any lattice quadrant of finite size.Like their row-to-row counterparts, corner transfer matrices may be factored into face transfer matrices, which correspond to adding a single face to the lattice. For the lattice quadrant given earlier, the face transfer matrices are of size 2m×2m and defined entry-wise by
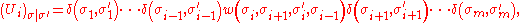
where 2 ≤ i ≤ m+1. Near the outer boundary, specifically, we have
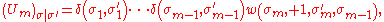

So the corner transfer matrix A factorises as

where

Graphically, this corresponds to:
We also require the 2m×2m matrices A* and A**, defined entry-wise by
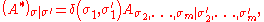
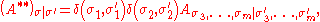
where the A matrices whose entries appear on the RHS are of size 2m-1×2m-1 and 2m-2×2m-2 respectively. This is more clearly written as
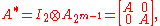

Now from the definitions of A, A*, A**, Ui and Fj, we have

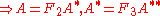

which gives the recursion relation for A2m in terms of A2m-1 and A2m-2.
Diagonal form
When using corner transfer matrices to perform calculations, it is both analytically and numerically convenient to work with their diagonal forms instead. To facilitate this, the recursion relation may be rewritten directly in terms of the diagonal forms and eigenvector matrices of A, A* and A**.Recalling that the lattice in our example is reflection-invariant, in the sense that
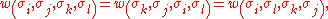
we see that A is a symmetric matrix (i.e. it is diagonalisable by an orthogonal matrix). So we write

where Ad is a diagonal matrix (normalised such that its numerically largest entry is 1), αm is the largest eigenvalue of A, and PTP = I. Likewise for A* and A**, we have

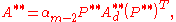
where Ad*, Ad**, P* and P** are defined in an analogous fashion to A* and A**, i.e. in terms of the smaller (normalised) diagonal forms and (orthogonal) eigenvector matrices of A2m-1 and A2m-2.
By substituting these diagonalisations into the recursion relation, we obtain

where
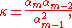

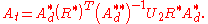
Now At is also symmetric, and may be calculated if Ad*, Ad** and R* are known; diagonalising At then yields its normalised diagonal form Ad, its largest eigenvalue κ, and its orthogonal eigenvector matrix R.
Spin expectation value
Corner transfer matrices (or their diagonal forms) may be used to calculate quantities such as the spin expectation valueExpected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
at a particular site deep inside the lattice. For the full lattice given earlier, the spin expectation value at the central site is given by

With the configurations ordered such that A is block diagonal as before, we may define a 2m×2m diagonal matrix
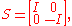
such that
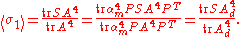
Partition function per site
Another important quantity for lattice models is the partition function per site, evaluated in the thermodynamic limitThermodynamic limit
In thermodynamics, particularly statistical mechanics, the thermodynamic limit is reached as the number of particles in a system, N, approaches infinity...
and written as

In our example, this reduces to

since tr Ad4 is a convergent sum as m → ∞ and Ad becomes infinite-dimensional. Furthermore, the number of faces 2m(m+1) approaches the number of sites N in the thermodynamic limit, so we have

which is consistent with the earlier equation giving κ as the largest eigenvalue for At. In other words, the partition function per site is given exactly by the diagonalised recursion relation for corner transfer matrices in the thermodynamic limit; this allows κ to be approximated via the iterative process of calculating Ad for a large lattice.
The matrices involved grow exponentially in size, however, and in actual numerical calculations they must be truncated at each step. One way of doing this is to keep the n largest eigenvalues at each step, for some fixed n. In most cases, the sequence of approximations obtained by taking n = 1,2,3,… converges rapidly, and to the exact value (for an exactly solvable model).

