
Complete quotient
Encyclopedia
In the metrical theory of regular continued fractions
, the kth complete quotient ζ k is obtained by ignoring the first k partial denominators ai. For example, if a regular continued fraction is given by
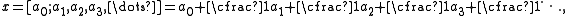
then the successive complete quotients ζ k are given by
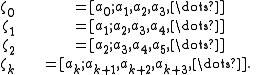
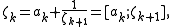
or, equivalently,

s of the regular continued fraction x = [a0; a1, a2, …] by A0, A1/B1, A2/B2, … (as explained more fully in the article fundamental recurrence formulas
), it can be shown that

for all k ≥ 0.
This result can be better understood by recalling that the successive convergents of an infinite regular continued fraction approach the value x in a sort of zig-zag pattern:
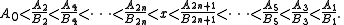
so that when k is even we have Ak/Bk < x < Ak+1/Bk+1, and when k is odd we have Ak+1/Bk+1 < x < Ak/Bk. In either case, the k + 1st complete quotient ζ k+1 is the unique real number that expresses x in the form of a semiconvergent.

where a, b, c, and d are integer
s, and ad − bc = ±1. Since this set of LFTs contains an identity element (0 + x)/1, and since it is closed under composition of functions, and every member of the set has an inverse in the set, these LFTs form a group
(the group operation being composition of functions).
We can define an equivalence relation
on the set of real number
s by means of this group of linear fractional transformations. We will say that two real numbers x and y are equivalent (written x ~ y) if
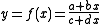
for some integers a, b, c, and d such that ad − bc = ±1.
Clearly this relation is symmetric, reflexive, and transitive, so it is an equivalence relation and it can be used to separate the real numbers into equivalence classes. All the rational number
s are equivalent, because each rational number is equivalent to zero. What can be said about the irrational number
s? Do they also fall into a single equivalence class?
Let x and y be two irrational (real) numbers, and let the kth complete quotient in the regular continued fraction expansions of x and y be denoted by ζ k and ψ k, respectively, Then x ~ y (under the equivalence defined in the preceding section) if and only if there are positive integers m and n such that ζ m = ψ n.
φ is the irrational number with the very simplest possible expansion as a regular continued fraction: φ = [1; 1, 1, 1, …]. The theorem tells us first that if x is any real number whose expansion as a regular continued fraction contains the infinite string
[1, 1, 1, 1, …], then there are integers a, b, c, and d (with ad − bc = ±1) such that
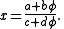
Conversely, if a, b, c, and d are integers (with ad − bc = ±1), then the regular continued fraction expansion of every real number y that can be expressed in the form
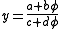
eventually reaches a "tail" that looks just like the regular continued fraction for φ.
Continued fraction
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on...
, the kth complete quotient ζ k is obtained by ignoring the first k partial denominators ai. For example, if a regular continued fraction is given by
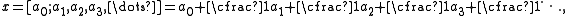
then the successive complete quotients ζ k are given by
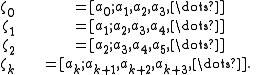
A recursive relationship
From the definition given above we can immediately deduce that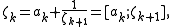
or, equivalently,

Complete quotients and the convergents of x
Denoting the successive convergentConvergent (continued fraction)
A convergent is one of a sequence of values obtained by evaluating successive truncations of a continued fraction The nth convergent is also known as the nth approximant of a continued fraction.-Representation of real numbers:...
s of the regular continued fraction x = [a0; a1, a2, …] by A0, A1/B1, A2/B2, … (as explained more fully in the article fundamental recurrence formulas
Fundamental recurrence formulas
In the theory of continued fractions, the fundamental recurrence formulas relate the partial numerators and the partial denominators with the numerators and denominators of the fraction's successive convergents...
), it can be shown that

for all k ≥ 0.
This result can be better understood by recalling that the successive convergents of an infinite regular continued fraction approach the value x in a sort of zig-zag pattern:
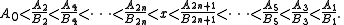
so that when k is even we have Ak/Bk < x < Ak+1/Bk+1, and when k is odd we have Ak+1/Bk+1 < x < Ak/Bk. In either case, the k + 1st complete quotient ζ k+1 is the unique real number that expresses x in the form of a semiconvergent.
An equivalence relation defined by LFTs
Consider the set of linear fractional transformations (LFTs) defined by
where a, b, c, and d are integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s, and ad − bc = ±1. Since this set of LFTs contains an identity element (0 + x)/1, and since it is closed under composition of functions, and every member of the set has an inverse in the set, these LFTs form a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
(the group operation being composition of functions).
We can define an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
on the set of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s by means of this group of linear fractional transformations. We will say that two real numbers x and y are equivalent (written x ~ y) if
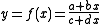
for some integers a, b, c, and d such that ad − bc = ±1.
Clearly this relation is symmetric, reflexive, and transitive, so it is an equivalence relation and it can be used to separate the real numbers into equivalence classes. All the rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s are equivalent, because each rational number is equivalent to zero. What can be said about the irrational number
Irrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
s? Do they also fall into a single equivalence class?
A theorem about "equivalent" irrational numbers
Amazingly enough, two irrational numbers x and y are equivalent under this scheme if and only if the infinitely long "tails" in their expansions as regular continued fractions are exactly the same. More precisely, the following theorem can be proved.Let x and y be two irrational (real) numbers, and let the kth complete quotient in the regular continued fraction expansions of x and y be denoted by ζ k and ψ k, respectively, Then x ~ y (under the equivalence defined in the preceding section) if and only if there are positive integers m and n such that ζ m = ψ n.
An example
The golden ratioGolden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
φ is the irrational number with the very simplest possible expansion as a regular continued fraction: φ = [1; 1, 1, 1, …]. The theorem tells us first that if x is any real number whose expansion as a regular continued fraction contains the infinite string
[1, 1, 1, 1, …], then there are integers a, b, c, and d (with ad − bc = ±1) such that
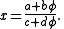
Conversely, if a, b, c, and d are integers (with ad − bc = ±1), then the regular continued fraction expansion of every real number y that can be expressed in the form
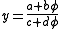
eventually reaches a "tail" that looks just like the regular continued fraction for φ.

