
Choi's theorem on completely positive maps
Encyclopedia
In mathematics
, Choi's theorem on completely positive maps (after Man-Duen Choi) is a result that classifies completely positive maps between finite-dimensional (matrix) C*-algebras. An infinite-dimensional algebraic generalization of Choi's theorem is known as Belavkin
's "Radon–Nikodym" theorem for completely positive maps.
of A is nonnegative. (This condition is also called positive semidefinite
.)
A linear map Φ : Cn × n → Cm × m is said to be a positive map if Φ(A) ≥ 0 for all A ≥ 0. In other words, a map Φ is positive if it preserves Hermiticity and the cone of positive elements.
Any linear map Φ induces another map
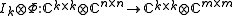
in a natural way: define
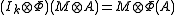
and extend by linearity. In matrix notation, a general element in
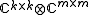
can be expressed as a k × k operator matrix:
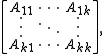
and its image under the induced map is
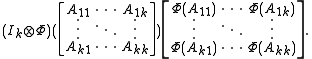
Writing out the individual elements in the above matrix-of-matrices amounts to the natural identification of algebras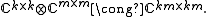
We say that Φ is k-positive if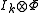 , considered as an element of Ckm×km, is a positive map, and Φ is called completely positive
, considered as an element of Ckm×km, is a positive map, and Φ is called completely positive
if Φ is k-positive for all k.
The transposition map
is a standard example of a positive map that fails to be 2-positive. Let T denote this map on C 2 × 2. The following is a positive matrix in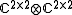 :
:
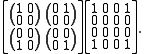
The image of this matrix under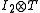 is
is
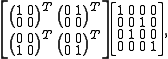
which is clearly not positive, having determinant -1.
Incidentally, a map Φ is said to be co-positive if the composition Φ T is positive. The transposition map itself is a co-positive map.
T is positive. The transposition map itself is a co-positive map.
The above notions concerning positive maps extend naturally to maps between C*-algebras.
Let

be a positive map. The following are equivalent:
i)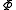 is n-positive.
is n-positive.
ii) The matrix with operator entries
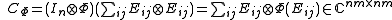
is positive, where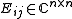 is the matrix with 1 in the
is the matrix with 1 in the 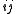 -th entry and 0s elsewhere. (The matrix
-th entry and 0s elsewhere. (The matrix  is sometimes called the Choi matrix of
is sometimes called the Choi matrix of 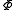 .)
.)
iii)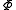 is completely positive.
is completely positive.
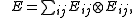
then E=E* and E2=nE, so E=n-1EE* which is positive and
CΦ=(In⊗Φ)(E) is positive by the n-positivity of Φ.
If iii) holds, then so does i) trivially.
We now turn to the argument for ii) ⇒ iii). This mainly involves chasing the different ways of looking at Cnm×nm: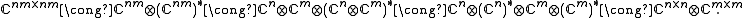
Let the eigenvector decomposition of CΦ be
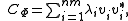
where the vectors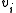 lie in Cnm . By assumption, each eigenvalue
lie in Cnm . By assumption, each eigenvalue 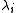 is non-negative so we can absorb the eigenvalues in the eigenvectors and redefine
is non-negative so we can absorb the eigenvalues in the eigenvectors and redefine 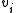 so that
so that
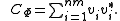
The vector space Cnm can be viewed as the direct sum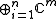
compatibly with the above identification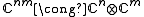
and the standard basis of Cn.
If Pk ∈ Cm × nm is projection onto the k-th copy of Cm, then Pk* ∈ Cnm×m
is the inclusion of Cm as the k-th summand of the direct sum and
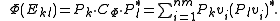
Now if the operators Vi ∈ Cm×n are defined on the k-th standard
basis vector ek of Cn by
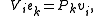
then

Extending by linearity gives us
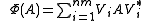
for any A ∈ Cn × n. Since any map of this form is manifestly completely positive, we have the desired result.
The above is essentially Choi's original proof. Alternative proofs have also been known.
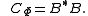
gives a set of Kraus operators. (Notice B need not be the unique positive square root
of the Choi matrix.)
Let
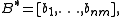
where bi*'s are the row vectors of B, then
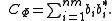
The corresponding Kraus operators can be obtained by exactly the same argument from the proof.
When the Kraus operators are obtained from the eigenvector decomposition of the Choi matrix, because the eigenvectors form an orthogonal set, the corresponding Kraus operators are also orthogonal in the Hilbert–Schmidt inner product. This is not true in general for Kraus operators obtained from square root factorizations. (Positive semidefinite matrices do not generally have a unique square-root factorizations.)
If two sets of Kraus operators {Ai}1nm and {Bi}1nm represent the same completely positive map Φ, then there exists a unitary operator matrix

This can be viewed as a special case of the result relating two minimal Stinespring representations
.
Alternatively, there is an isometry scalar matrix {uij}ij ∈ Cnm × nm such that
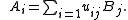
This follows from the fact that for two square matrices M and N, M M* = N N* if and only if M = N U for some unitary U.
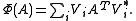

where λi are real numbers, the eigenvalues of CΦ,
and each Vi corresponds to an eigenvector of CΦ. Unlike the completely positive case, CΦ may fail to be positive. Since Hermitian matrices do not admit factorizations of the form B*B in general, the Kraus representation is no longer possible for a given Φ.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Choi's theorem on completely positive maps (after Man-Duen Choi) is a result that classifies completely positive maps between finite-dimensional (matrix) C*-algebras. An infinite-dimensional algebraic generalization of Choi's theorem is known as Belavkin
Viacheslav Belavkin
Viacheslav Pavlovich Belavkin is a professor in applied mathematics at the University of Nottingham. He was born in Lwów, and graduated from Moscow State University in 1970. In 1996, he and Ruslan L. Stratonovich were awarded the Main State Prize of the Russian Federation for outstanding...
's "Radon–Nikodym" theorem for completely positive maps.
Some preliminary notions
Before stating Choi's result, we give the definition of a completely positive map and fix some notation. Cn × n will denote the C*-algebra of n × n complex matrices. We will call A ∈ Cn × n positive, or symbolically, A ≥ 0, if A is Hermitian and the spectrumSpectrum of a matrix
In mathematics, the spectrum of a matrix is the set of its eigenvalues. This notion can be extended to the spectrum of an operator in the infinite-dimensional case.The determinant equals the product of the eigenvalues...
of A is nonnegative. (This condition is also called positive semidefinite
Positive semidefinite
In mathematics, positive semidefinite may refer to:* positive-semidefinite matrix* positive-semidefinite function...
.)
A linear map Φ : Cn × n → Cm × m is said to be a positive map if Φ(A) ≥ 0 for all A ≥ 0. In other words, a map Φ is positive if it preserves Hermiticity and the cone of positive elements.
Any linear map Φ induces another map
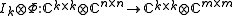
in a natural way: define
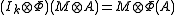
and extend by linearity. In matrix notation, a general element in
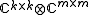
can be expressed as a k × k operator matrix:
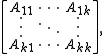
and its image under the induced map is
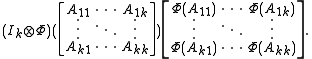
Writing out the individual elements in the above matrix-of-matrices amounts to the natural identification of algebras
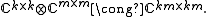
We say that Φ is k-positive if
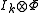 , considered as an element of Ckm×km, is a positive map, and Φ is called completely positive
, considered as an element of Ckm×km, is a positive map, and Φ is called completely positiveif Φ is k-positive for all k.
The transposition map
Transpose
In linear algebra, the transpose of a matrix A is another matrix AT created by any one of the following equivalent actions:...
is a standard example of a positive map that fails to be 2-positive. Let T denote this map on C 2 × 2. The following is a positive matrix in
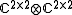 :
: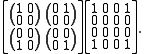
The image of this matrix under
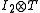 is
is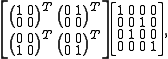
which is clearly not positive, having determinant -1.
Incidentally, a map Φ is said to be co-positive if the composition Φ
 T is positive. The transposition map itself is a co-positive map.
T is positive. The transposition map itself is a co-positive map.The above notions concerning positive maps extend naturally to maps between C*-algebras.
Statement of theorem
Choi's theorem reads as follows:Let

be a positive map. The following are equivalent:
i)
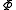 is n-positive.
is n-positive.ii) The matrix with operator entries
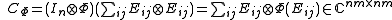
is positive, where
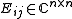 is the matrix with 1 in the
is the matrix with 1 in the 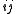 -th entry and 0s elsewhere. (The matrix
-th entry and 0s elsewhere. (The matrix  is sometimes called the Choi matrix of
is sometimes called the Choi matrix of 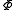 .)
.)iii)
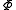 is completely positive.
is completely positive.Proof
To show i) implies ii), we observe that if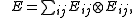
then E=E* and E2=nE, so E=n-1EE* which is positive and
CΦ=(In⊗Φ)(E) is positive by the n-positivity of Φ.
If iii) holds, then so does i) trivially.
We now turn to the argument for ii) ⇒ iii). This mainly involves chasing the different ways of looking at Cnm×nm:
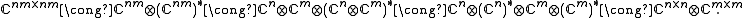
Let the eigenvector decomposition of CΦ be
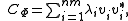
where the vectors
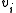 lie in Cnm . By assumption, each eigenvalue
lie in Cnm . By assumption, each eigenvalue 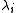 is non-negative so we can absorb the eigenvalues in the eigenvectors and redefine
is non-negative so we can absorb the eigenvalues in the eigenvectors and redefine 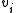 so that
so that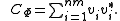
The vector space Cnm can be viewed as the direct sum
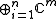
compatibly with the above identification
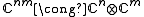
and the standard basis of Cn.
If Pk ∈ Cm × nm is projection onto the k-th copy of Cm, then Pk* ∈ Cnm×m
is the inclusion of Cm as the k-th summand of the direct sum and
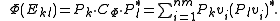
Now if the operators Vi ∈ Cm×n are defined on the k-th standard
basis vector ek of Cn by
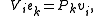
then

Extending by linearity gives us
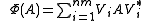
for any A ∈ Cn × n. Since any map of this form is manifestly completely positive, we have the desired result.
The above is essentially Choi's original proof. Alternative proofs have also been known.
Kraus operators
In the context of quantum information theory, the operators {Vi} are called the Kraus operators (after Karl Kraus) of Φ. Notice, given a completely positive Φ, its Kraus operators need not be unique. For example, any "square root" factorization of the Choi matrix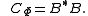
gives a set of Kraus operators. (Notice B need not be the unique positive square root
Square root of a matrix
In mathematics, the square root of a matrix extends the notion of square root from numbers to matrices. A matrix B is said to be a square root of A if the matrix product B · B is equal to A.-Properties:...
of the Choi matrix.)
Let
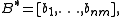
where bi*'s are the row vectors of B, then
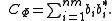
The corresponding Kraus operators can be obtained by exactly the same argument from the proof.
When the Kraus operators are obtained from the eigenvector decomposition of the Choi matrix, because the eigenvectors form an orthogonal set, the corresponding Kraus operators are also orthogonal in the Hilbert–Schmidt inner product. This is not true in general for Kraus operators obtained from square root factorizations. (Positive semidefinite matrices do not generally have a unique square-root factorizations.)
If two sets of Kraus operators {Ai}1nm and {Bi}1nm represent the same completely positive map Φ, then there exists a unitary operator matrix

This can be viewed as a special case of the result relating two minimal Stinespring representations
Stinespring factorization theorem
In mathematics, Stinespring's dilation theorem, also called Stinespring's factorization theorem, named after W. Forrest Stinespring, is a result from operator theory that represents any completely positive map on a C*-algebra as a composition of two completely positive maps each of which has a...
.
Alternatively, there is an isometry scalar matrix {uij}ij ∈ Cnm × nm such that
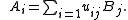
This follows from the fact that for two square matrices M and N, M M* = N N* if and only if M = N U for some unitary U.
Completely copositive maps
It follows immediately from Choi's theorem that Φ is completely copositive if and only if it is of the form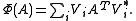
Hermitian-preserving maps
Choi's technique can be used to obtain a similar result for a more general class of maps. Φ is said to be Hermitian-preserving if A is Hermitian implies Φ(A) is also Hermitian. One can show Φ is Hermitian-preserving if and only if it is of the form
where λi are real numbers, the eigenvalues of CΦ,
and each Vi corresponds to an eigenvector of CΦ. Unlike the completely positive case, CΦ may fail to be positive. Since Hermitian matrices do not admit factorizations of the form B*B in general, the Kraus representation is no longer possible for a given Φ.

