Cauchy's theorem (group theory)
Encyclopedia
Cauchy's theorem is a theorem in the mathematics of group theory
, named after Augustin Louis Cauchy
. It states that if G is a finite group
and p is a prime number
dividing the order
of G (the number of elements in G), then G contains an element of order p. That is, there is x in G so that p is the lowest non-zero number with xp = e, where e is the identity element
.
The theorem is related to Lagrange's theorem
, which states that the order of any subgroup
of a finite group G divides the order of G. Cauchy's theorem implies that for any prime divisor p of the order of G, there is a subgroup of G whose order is p—the cyclic group
generated by the element in Cauchy's theorem.
Cauchy's theorem is generalised by Sylow's first theorem, which implies that if pn is any prime power dividing the order of G, then G has a subgroup of order pn.
case. One can also invoke group actions for the proof.
Theorem: Let G be a finite group
and p be a prime
. If p divides the order
of G, then G has an element of order p.
Proof 1: We induct on n = |G| and consider the two cases where G is abelian
or G is nonabelian
. Suppose G is abelian. If G is simple
, then it must be cyclic
of prime order and trivially contains an element of order p. Otherwise, there exists a nontrivial, proper normal subgroup
. If p divides |H|, then H contains an element of order p by the inductive hypothesis, and thus G does as well. Otherwise, p must divide the index
[G:H] by Lagrange's theorem
, and we see the quotient group
G/H contains an element of order p by the inductive hypothesis; that is, there exists an x in G such that (Hx)p = Hxp = H. Then there exists an element h1 in H such that h1xp = 1, the identity element of G. It is easily checked that for every element a in H there exists b in H such that bp = a, so there exists h2 in H so that h2 p = h1. Thus h2x has order p, and the proof is finished for the abelian case.
Suppose that G is nonabelian, so that its center
Z is a proper subgroup. If p divides the order of the centralizer CG(a) for some noncentral element a (i.e. a is not in Z), then CG(a) is a proper subgroup and hence contains an element of order p by the inductive hypothesis. Otherwise, we must have p dividing the index [G:CG(a)], again by Lagrange's Theorem, for all noncentral a. Using the class equation, we have p dividing the left side of the equation (|G|) and also dividing all of the summands on the right, except for possibly |Z|. However, simple arithmetic shows p must also divide the order of Z, and thus the center contains an element of order p by the inductive hypothesis as it is a proper subgroup and hence of order strictly less than that of G. This completes the proof.
Proof 2: This time we define the set of p-tuples whose elements are in the group G by
.
Note that we can choose only (p-1) of the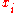
independently, since we are constrained by the product equal to the identity. Thus 
, from which we deduce that p also divides 
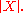
Define the action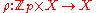
by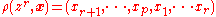 
, where 
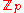is the cyclic group of order p.
Then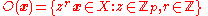
is the orbit of some element 
.
The stabilizer is
, from which we can deduce the order,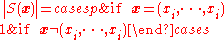 
.
We have from the Orbit-Stabilizer Theorem that
for each 
.
Take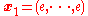
and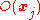 
the distinct orbits. Then 
.
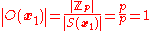Hence we know that
.
p divides |X| implies that there is at least one other
with the property that its orbit has order 1.
Then we have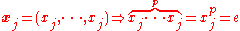
by the definition of X.
Since xj is in G this completes the proof.
, where p is a prime. In particular, a finite group G is a p-group (i.e. all of its elements have order pk for some natural number
k) if and only if G has order pn for some natural number n. It is also typical to use Cauchy's Theorem to prove the first of Sylow's Theorems, though this is not required.
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, named after Augustin Louis Cauchy
Augustin Louis Cauchy
Baron Augustin-Louis Cauchy was a French mathematician who was an early pioneer of analysis. He started the project of formulating and proving the theorems of infinitesimal calculus in a rigorous manner, rejecting the heuristic principle of the generality of algebra exploited by earlier authors...
. It states that if G is a finite group
Finite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
and p is a prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
dividing the order
Order (group theory)
In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
of G (the number of elements in G), then G contains an element of order p. That is, there is x in G so that p is the lowest non-zero number with xp = e, where e is the identity element
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
.
The theorem is related to Lagrange's theorem
Lagrange's theorem (group theory)
Lagrange's theorem, in the mathematics of group theory, states that for any finite group G, the order of every subgroup H of G divides the order of G. The theorem is named after Joseph Lagrange....
, which states that the order of any subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of a finite group G divides the order of G. Cauchy's theorem implies that for any prime divisor p of the order of G, there is a subgroup of G whose order is p—the cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
generated by the element in Cauchy's theorem.
Cauchy's theorem is generalised by Sylow's first theorem, which implies that if pn is any prime power dividing the order of G, then G has a subgroup of order pn.
Statement and proof
Many texts appear to prove the theorem with the use of strong induction and the class equation, though considerably less machinery is required to prove the theorem in the abelianAbelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
case. One can also invoke group actions for the proof.
Theorem: Let G be a finite group
Finite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
and p be a prime
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
. If p divides the order
Order (group theory)
In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
of G, then G has an element of order p.
Proof 1: We induct on n = |G| and consider the two cases where G is abelian
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
or G is nonabelian
Nonabelian group
In mathematics, a non-abelian group, also sometimes called a non-commutative group, is a group in which there are at least two elements a and b of G such that a * b ≠ b * a...
. Suppose G is abelian. If G is simple
Simple group
In mathematics, a simple group is a nontrivial group whose only normal subgroups are the trivial group and the group itself. A group that is not simple can be broken into two smaller groups, a normal subgroup and the quotient group, and the process can be repeated...
, then it must be cyclic
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
of prime order and trivially contains an element of order p. Otherwise, there exists a nontrivial, proper normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
. If p divides |H|, then H contains an element of order p by the inductive hypothesis, and thus G does as well. Otherwise, p must divide the indexIndex of a subgroup
In mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...
[G:H] by Lagrange's theorem
Lagrange's theorem (group theory)
Lagrange's theorem, in the mathematics of group theory, states that for any finite group G, the order of every subgroup H of G divides the order of G. The theorem is named after Joseph Lagrange....
, and we see the quotient group
Quotient group
In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
G/H contains an element of order p by the inductive hypothesis; that is, there exists an x in G such that (Hx)p = Hxp = H. Then there exists an element h1 in H such that h1xp = 1, the identity element of G. It is easily checked that for every element a in H there exists b in H such that bp = a, so there exists h2 in H so that h2 p = h1. Thus h2x has order p, and the proof is finished for the abelian case.
Suppose that G is nonabelian, so that its center
Center (group theory)
In abstract algebra, the center of a group G, denoted Z,The notation Z is from German Zentrum, meaning "center". is the set of elements that commute with every element of G. In set-builder notation,...
Z is a proper subgroup. If p divides the order of the centralizer CG(a) for some noncentral element a (i.e. a is not in Z), then CG(a) is a proper subgroup and hence contains an element of order p by the inductive hypothesis. Otherwise, we must have p dividing the index [G:CG(a)], again by Lagrange's Theorem, for all noncentral a. Using the class equation, we have p dividing the left side of the equation (|G|) and also dividing all of the summands on the right, except for possibly |Z|. However, simple arithmetic shows p must also divide the order of Z, and thus the center contains an element of order p by the inductive hypothesis as it is a proper subgroup and hence of order strictly less than that of G. This completes the proof.
Proof 2: This time we define the set of p-tuples whose elements are in the group G by
.Note that we can choose only (p-1) of the
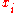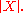
independently, since we are constrained by the product equal to the identity. Thus , from which we deduce that p also divides Define the action
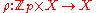by 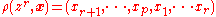, where 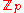is the cyclic group of order p. Then
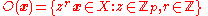is the orbit of some element .The stabilizer is
, from which we can deduce the order, 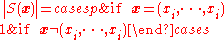.We have from the Orbit-Stabilizer Theorem that
for each .Take
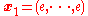and 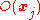the distinct orbits. Then 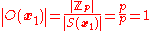. Hence we know that
. p divides |X| implies that there is at least one other
with the property that its orbit has order 1.Then we have
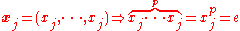by the definition of X. Since xj is in G this completes the proof.
Uses
A practically immediate consequence of Cauchy's Theorem is a useful characterization of finite p-groupsP-group
In mathematics, given a prime number p, a p-group is a periodic group in which each element has a power of p as its order: each element is of prime power order. That is, for each element g of the group, there exists a nonnegative integer n such that g to the power pn is equal to the identity element...
, where p is a prime. In particular, a finite group G is a p-group (i.e. all of its elements have order pk for some natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
k) if and only if G has order pn for some natural number n. It is also typical to use Cauchy's Theorem to prove the first of Sylow's Theorems, though this is not required.