
Camassa–Holm equation
Encyclopedia

Fluid dynamics
In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...
, the Camassa–Holm equation is the integrable
Integrable system
In mathematics and physics, there are various distinct notions that are referred to under the name of integrable systems.In the general theory of differential systems, there is Frobenius integrability, which refers to overdetermined systems. In the classical theory of Hamiltonian dynamical...
, dimensionless
Dimensionless quantity
In dimensional analysis, a dimensionless quantity or quantity of dimension one is a quantity without an associated physical dimension. It is thus a "pure" number, and as such always has a dimension of 1. Dimensionless quantities are widely used in mathematics, physics, engineering, economics, and...
and non-linear partial differential equation

The equation was introduced by Camassa and Holm as a bi-Hamiltonian
Hamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
model for waves in shallow water
Waves and shallow water
When waves travel into areas of shallow water, they begin to be affected by the ocean bottom. The free orbital motion of the water is disrupted, and water particles in orbital motion no longer return to their original position. As the water becomes shallower, the swell becomes higher and steeper,...
, and in this context the parameter κ is positive and the solitary wave
Solitary wave
In mathematics and physics, a solitary wave can refer to* The solitary wave or wave of translation, as observed by John Scott Russell in the Union Canal, near Edinburgh in 1834...
solutions are smooth solitons.
In the special case that κ is equal to zero, the Camassa–Holm equation has peakon solutions: solitons with a sharp peak, so with a discontinuity at the peak in the wave slope
Slope
In mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline....
.
Relation to waves in shallow water
The Camassa–Holm equation can be written as the system of equations: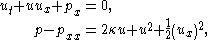
with p the (dimensionless) pressure or surface elevation. This shows that the Camassa–Holm equation is a model for shallow water waves with non-hydrostatic pressure and a water layer on a horizontal bed.
The linear dispersion
Dispersion (water waves)
In fluid dynamics, dispersion of water waves generally refers to frequency dispersion, which means that waves of different wavelengths travel at different phase speeds. Water waves, in this context, are waves propagating on the water surface, and forced by gravity and surface tension...
characteristics of the Camassa–Holm equation are:
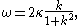
with ω the angular frequency
Angular frequency
In physics, angular frequency ω is a scalar measure of rotation rate. Angular frequency is the magnitude of the vector quantity angular velocity...
and k the wavenumber
Wavenumber
In the physical sciences, the wavenumber is a property of a wave, its spatial frequency, that is proportional to the reciprocal of the wavelength. It is also the magnitude of the wave vector...
. Not surprisingly, this is of similar form as the one for the Korteweg–de Vries equation
Korteweg–de Vries equation
In mathematics, the Korteweg–de Vries equation is a mathematical model of waves on shallow water surfaces. It is particularly notable as the prototypical example of an exactly solvable model, that is, a non-linear partial differential equation whose solutions can be exactly and precisely specified...
, provided κ is unequal to zero. For κ equal to zero, the Camassa–Holm equation has no frequency dispersion — moreover, the linear phase speed is zero for this case. As a result, κ is the phase speed for the long-wave limit of k approaching zero, and the Camassa–Holm equation is (if κ is non-zero) a model for one-directional wave propagation like the Korteweg–de Vries equation.
Hamiltonian structure
Introducing the momentum m as
then two compatible Hamiltonian
Hamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
descriptions of the Camassa–Holm equation are:
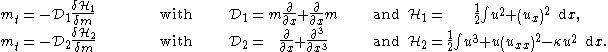
Integrability
The Camassa–Holm equation is an integrable systemIntegrable system
In mathematics and physics, there are various distinct notions that are referred to under the name of integrable systems.In the general theory of differential systems, there is Frobenius integrability, which refers to overdetermined systems. In the classical theory of Hamiltonian dynamical...
. Integrability means that there is a change of variables (action-angle variables) such that the evolution equation in the new variables is equivalent to a linear flow at constant speed. This change of variables is achieved by studying an associated isospectral/scattering problem
Inverse scattering transform
In mathematics, the inverse scattering transform is a method for solving some non-linear partial differential equations. It is one of the most important developments in mathematical physics in the past 40 years...
, and is reminiscent of the fact that integrable classical Hamiltonian system
Hamiltonian system
In physics and classical mechanics, a Hamiltonian system is a physical system in which forces are momentum invariant. Hamiltonian systems are studied in Hamiltonian mechanics....
s are equivalent to linear flows at constant speed on tori
Tori
Tori may refer to:*Taiwan Ocean Research Institute, the ocean research institute of Taiwan*Tori , horse originating in continental Estonia*Tori , the executor of a technique in partnered martial arts practice...
. The Camassa–Holm equation is integrable provided that the momentum
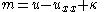
is positive — see and for a detailed description of the spectrum
Spectrum
A spectrum is a condition that is not limited to a specific set of values but can vary infinitely within a continuum. The word saw its first scientific use within the field of optics to describe the rainbow of colors in visible light when separated using a prism; it has since been applied by...
associated to the isospectral problem, for the inverse spectral problem in the case of spatially periodic smooth solutions, and for the inverse scattering approach in the case of smooth solutions that decay at infinity.
Exact solutions
Traveling waves are solutions of the form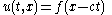
representing waves of permanent shape f that propagate at constant speed c. These waves are called solitary waves if they are localized disturbances, that is, if the wave profile f decays at infinity. If the solitary waves retain their shape and speed after interacting with other waves of the same type, we say that
the solitary waves are solitons. There is a close connection between integrability and solitons.
In the limiting case when κ = 0 the solitons become peaked (shaped like the graph of the function f(x) = e-|x|), and they are then called peakons. It is possible to provide explicit formulas for the peakon interactions, visualizing thus the fact that they are solitons. For the smooth solitons the soliton interactions are less elegant. This is due in part to the fact that, unlike the peakons, the smooth solitons are relatively easy to describe qualitatively — they are smooth, decaying exponentially fast at infinity, symmetric with respect to the crest, and with two inflection points — but explicit formulas are not available. Notice also that the solitary waves are orbitally stable i.e. their shape is stable under small perturbations, both for the smooth solitons and for the peakons.
Wave breaking
The Camassa–Holm equation models breaking waveBreaking wave
In fluid dynamics, a breaking wave is a wave whose amplitude reaches a critical level at which some process can suddenly start to occur that causes large amounts of wave energy to be transformed into turbulent kinetic energy...
s: a smooth initial profile with sufficient decay at infinity develops into either a wave that exists for all times or into a breaking wave (wave breaking being characterized by the fact that the solution remains bounded but its slope becomes unbounded in finite time). The fact that the equations admits solutions of this type was discovered by Camassa and Holm and these considerations were subsequently put on a firm mathematical basis.
It is known that the only way singularities can occur in solutions is in the form of breaking waves.
Moreover, from the knowledge of a smooth initial profile it is possible to predict (via a necessary and sufficient condition) whether wave breaking occurs or not.
As for the continuation of solutions after wave breaking, two scenarios are possible: the conservative case
and the dissipative case
(with the first characterized by conservation of the energy, while the dissipative scenario accounts for loss of energy due to breaking).
Long-time asymptotics
It can be shown that for sufficiently fast decaying smooth initial conditions with positive momentum splits into a finite number and solitons plus a decaying dispersive part. More precisely, one can show the following for :
:Abbreviate
 . In the soliton region
. In the soliton region  the solutions splits into a finite linear combination solitons. In the region
the solutions splits into a finite linear combination solitons. In the region 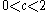 the solution is asymptotically given by a modulated sine function whose amplitude decays like
the solution is asymptotically given by a modulated sine function whose amplitude decays like 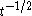 . In the region
. In the region  the solution is asymptotically given by a sum of two modulated sine function as in the previous case. In the region
the solution is asymptotically given by a sum of two modulated sine function as in the previous case. In the region 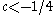 the solution decays rapidly.
the solution decays rapidly.Further reading
Peakon solutionsWater wave theory
Existence, uniqueness, wellposedness, stability, propagation speed, etc.
Travelling waves
Integrability structure (symmetries, hierarchy of soliton equations, conservations laws) and differential-geometric formulation

