
Bertrand's ballot theorem
Encyclopedia
In combinatorics
, Bertrand's ballot problem, named after Joseph Louis François Bertrand
who introduced it in 1887, is the question: "In an election
where candidate A receives p votes and candidate B q votes with p > q, what is the probability
that A will be strictly ahead of B throughout the count?". The answer is
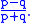
In Bertrand's original paper, he sketched a proof based on a general formula for the number of favourable sequences, based on a recursion relation. Although he does not explicitly give this formula, it can be seen to be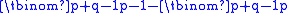 ; indeed after division by the total number
; indeed after division by the total number  of possible sequences this gives
of possible sequences this gives  .
.
He then remarks that it seems probable that such a simple result could be proved by a more direct method. Such a proof was given by Désiré André, based on the observation that the unfavourable sequences can be divided into two equally probable cases, one of which (the case where B receives the first vote) is easily computed; he proves the equality by an explicit bijection. A variation of his method is popularly known as André's reflection method, although André did not use any reflections.
The formula can be used to calculate the number of random walk
s on the integer
s of n steps, from the origin to the point m, that never become negative. Assuming n and m have the same parity and n ≥ m ≥ 0, this number is
When m = 0 and n is even, this gives the Catalan number
 .
.
For the order AABAB the tally of the votes as the election progresses is:
For each column the tally for A is always larger than the tally for B so the A is always strictly ahead of B. For the order AABBA the tally of the votes as the election progresses is:
For this order, B is tied with A after the fourth vote, so A is not always strictly ahead of B.
Of the 10 possible orders, A is always ahead of B only for AAABB and AABAB. So the probability the A will always be strictly ahead is
as the theorem predicts.
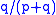 , so the probability that A always leads the vote is
, so the probability that A always leads the vote is
:
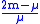
where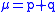 is the total number of voters and
is the total number of voters and  is the number of voters for the first candidate. He states that the result follows from the formula
is the number of voters for the first candidate. He states that the result follows from the formula ,
,
where is the number of favourable sequences, but "it seems probable that such a simple result could be shown in a more direct way". Indeed, a more direct proof was soon produced by Désiré André. His approach is often mistakenly labelled "the reflection principle" by modern authors but in fact uses a permututation. He shows that the "unfavourable" sequences (those that reach an intermediate tie) consist of an equal number of sequences that begin with A as those that begin with B. Every sequence that begins with B is unfavourable, and there are
is the number of favourable sequences, but "it seems probable that such a simple result could be shown in a more direct way". Indeed, a more direct proof was soon produced by Désiré André. His approach is often mistakenly labelled "the reflection principle" by modern authors but in fact uses a permututation. He shows that the "unfavourable" sequences (those that reach an intermediate tie) consist of an equal number of sequences that begin with A as those that begin with B. Every sequence that begins with B is unfavourable, and there are 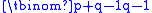 such sequences with a B followed by an arbitrary sequence of (q-1) B's and p A's. Each unfavourable sequence that begins with A can be transformed to an arbitrary sequence of (q-1) B's and p A's by finding the first B that violates the rule (by causing the vote counts to tie) and deleting it, and interchanging the order of the remaining parts. To reverse the process, take any sequence of (q-1) B's and p A's and search from the end to find where the number of A's first exceeds the number of B's, and then interchange the order of the parts and place a B in between. For example, the unfavourable sequence AABBABAA corresponds uniquely to the arbitrary sequence ABAAAAB. From this, it follows that the number of favourable sequences of p A's and q B's is
such sequences with a B followed by an arbitrary sequence of (q-1) B's and p A's. Each unfavourable sequence that begins with A can be transformed to an arbitrary sequence of (q-1) B's and p A's by finding the first B that violates the rule (by causing the vote counts to tie) and deleting it, and interchanging the order of the remaining parts. To reverse the process, take any sequence of (q-1) B's and p A's and search from the end to find where the number of A's first exceeds the number of B's, and then interchange the order of the parts and place a B in between. For example, the unfavourable sequence AABBABAA corresponds uniquely to the arbitrary sequence ABAAAAB. From this, it follows that the number of favourable sequences of p A's and q B's is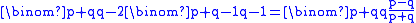
and thus the required probability is
as expected.
 .
.
The variant problem can be solved by the reflection method in a similar way to the original problem. First note that the number of possible vote sequences is . Call a sequence "bad" if the second candidate is ever ahead, and if the number of bad sequences can be enumerated then the number of "good" sequences can be found by subtraction and the probability can be computed.
. Call a sequence "bad" if the second candidate is ever ahead, and if the number of bad sequences can be enumerated then the number of "good" sequences can be found by subtraction and the probability can be computed.
Represent a voting sequence as a lattice path on the Cartesian plane as follows:
Each such path corresponds to a unique sequence of votes and will end at (p, q). A sequence is 'good' exactly when the corresponding path never goes above the diagonal line y = x; equivalently, a sequence is 'bad' exactly when the corresponding path touches the line y = x + 1.
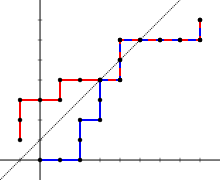 For each 'bad' path P, define a new path P′ by reflecting the part of P up to the first point it touches the line across it. P′ is a path from (−1, 1) to (p, q). The same operation applied again restores the original P. This produces a one-to-one correspondence between the 'bad' paths and the paths from (−1, 1) to (p, q). The number of these paths is
For each 'bad' path P, define a new path P′ by reflecting the part of P up to the first point it touches the line across it. P′ is a path from (−1, 1) to (p, q). The same operation applied again restores the original P. This produces a one-to-one correspondence between the 'bad' paths and the paths from (−1, 1) to (p, q). The number of these paths is 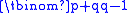 and so that is the number of 'bad' sequences. This leaves the number of 'good' sequences as
and so that is the number of 'bad' sequences. This leaves the number of 'good' sequences as
Since there are altogether, the probability of a sequence being good is
altogether, the probability of a sequence being good is 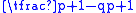 .
.
In fact, the solutions to the original problem and the variant problem are easily related. For candidate A to be strictly ahead throughout the vote count, they must receive the first vote and for the remaining votes (ignoring the first) they must be either strictly ahead or tied throughout the count. Hence the solution to the original problem is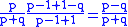
as required.
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
, Bertrand's ballot problem, named after Joseph Louis François Bertrand
Joseph Louis François Bertrand
Joseph Louis François Bertrand was a French mathematician who worked in the fields of number theory, differential geometry, probability theory, economics and thermodynamics....
who introduced it in 1887, is the question: "In an election
Election
An election is a formal decision-making process by which a population chooses an individual to hold public office. Elections have been the usual mechanism by which modern representative democracy operates since the 17th century. Elections may fill offices in the legislature, sometimes in the...
where candidate A receives p votes and candidate B q votes with p > q, what is the probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
that A will be strictly ahead of B throughout the count?". The answer is
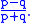
In Bertrand's original paper, he sketched a proof based on a general formula for the number of favourable sequences, based on a recursion relation. Although he does not explicitly give this formula, it can be seen to be
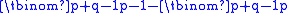 ; indeed after division by the total number
; indeed after division by the total number  of possible sequences this gives
of possible sequences this gives  .
.He then remarks that it seems probable that such a simple result could be proved by a more direct method. Such a proof was given by Désiré André, based on the observation that the unfavourable sequences can be divided into two equally probable cases, one of which (the case where B receives the first vote) is easily computed; he proves the equality by an explicit bijection. A variation of his method is popularly known as André's reflection method, although André did not use any reflections.
The formula can be used to calculate the number of random walk
Random walk
A random walk, sometimes denoted RW, is a mathematical formalisation of a trajectory that consists of taking successive random steps. For example, the path traced by a molecule as it travels in a liquid or a gas, the search path of a foraging animal, the price of a fluctuating stock and the...
s on the integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s of n steps, from the origin to the point m, that never become negative. Assuming n and m have the same parity and n ≥ m ≥ 0, this number is

When m = 0 and n is even, this gives the Catalan number
Catalan number
In combinatorial mathematics, the Catalan numbers form a sequence of natural numbers that occur in various counting problems, often involvingrecursively defined objects...
 .
.Example
Suppose there are 5 voters with 3 voting for candidate A and 2 voting for candidate B. So p=3 and q=2 in this example. Only the final result is known so there are ten possibilities for the order of the votes cast:- AAABB
- AABAB
- ABAAB
- BAAAB
- AABBA
- ABABA
- BAABA
- ABBAA
- BABAA
- BBAAA
For the order AABAB the tally of the votes as the election progresses is:
| Candidate | A | A | B | A | B |
| A | 1 | 2 | 2 | 3 | 3 |
| B | 0 | 0 | 1 | 1 | 2 |
For each column the tally for A is always larger than the tally for B so the A is always strictly ahead of B. For the order AABBA the tally of the votes as the election progresses is:
| Candidate | A | A | B | B | A |
| A | 1 | 2 | 2 | 2 | 3 |
| B | 0 | 0 | 1 | 2 | 2 |
For this order, B is tied with A after the fourth vote, so A is not always strictly ahead of B.
Of the 10 possible orders, A is always ahead of B only for AAABB and AABAB. So the probability the A will always be strictly ahead is

as the theorem predicts.
Proof by reflection
For A to be strictly ahead of B throughout the counting of the votes, there can be no ties. Separate the counting sequences according to the first vote. Any sequence that begins with a vote for B must reach a tie at some point, because A eventually wins. For any sequence that begins with A and reaches a tie, reflect the votes up to the point of the first tie (so any A becomes a B, and vice-versa) to obtain a sequence that begins with B. Hence every sequence that begins with A and reaches a tie is in one to one correspondence with a sequence that begins with B, and the probability that a sequence begins with B is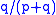 , so the probability that A always leads the vote is
, so the probability that A always leads the vote is
Proof by induction
Another method of proof is by mathematical inductionMathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
:
- Clearly the theorem is true if p > 0 and q = 0 when the probability is 1, given that the first candidate receives all the votes; it is also true when p = q > 0 since the probability is 0, given that the first candidate will not be strictly ahead after all the votes have been counted.
- Assume it is true both when p = a − 1 and q = b, and when p = a and q = b−1, with a > b > 0. Then considering the case with p = a and q = b, the last vote counted is either for the first candidate with probability a/(a + b), or for the second with probability b/(a + b). So the probability of the first being ahead throughout the count to the penultimate vote counted (and also after the final vote) is:
-

- And so it is true for all p and q with p > q > 0.
Bertrand's and André's proofs
Bertrand expressed the solution as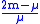
where
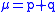 is the total number of voters and
is the total number of voters and  is the number of voters for the first candidate. He states that the result follows from the formula
is the number of voters for the first candidate. He states that the result follows from the formula ,
,where
 is the number of favourable sequences, but "it seems probable that such a simple result could be shown in a more direct way". Indeed, a more direct proof was soon produced by Désiré André. His approach is often mistakenly labelled "the reflection principle" by modern authors but in fact uses a permututation. He shows that the "unfavourable" sequences (those that reach an intermediate tie) consist of an equal number of sequences that begin with A as those that begin with B. Every sequence that begins with B is unfavourable, and there are
is the number of favourable sequences, but "it seems probable that such a simple result could be shown in a more direct way". Indeed, a more direct proof was soon produced by Désiré André. His approach is often mistakenly labelled "the reflection principle" by modern authors but in fact uses a permututation. He shows that the "unfavourable" sequences (those that reach an intermediate tie) consist of an equal number of sequences that begin with A as those that begin with B. Every sequence that begins with B is unfavourable, and there are 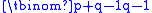 such sequences with a B followed by an arbitrary sequence of (q-1) B's and p A's. Each unfavourable sequence that begins with A can be transformed to an arbitrary sequence of (q-1) B's and p A's by finding the first B that violates the rule (by causing the vote counts to tie) and deleting it, and interchanging the order of the remaining parts. To reverse the process, take any sequence of (q-1) B's and p A's and search from the end to find where the number of A's first exceeds the number of B's, and then interchange the order of the parts and place a B in between. For example, the unfavourable sequence AABBABAA corresponds uniquely to the arbitrary sequence ABAAAAB. From this, it follows that the number of favourable sequences of p A's and q B's is
such sequences with a B followed by an arbitrary sequence of (q-1) B's and p A's. Each unfavourable sequence that begins with A can be transformed to an arbitrary sequence of (q-1) B's and p A's by finding the first B that violates the rule (by causing the vote counts to tie) and deleting it, and interchanging the order of the remaining parts. To reverse the process, take any sequence of (q-1) B's and p A's and search from the end to find where the number of A's first exceeds the number of B's, and then interchange the order of the parts and place a B in between. For example, the unfavourable sequence AABBABAA corresponds uniquely to the arbitrary sequence ABAAAAB. From this, it follows that the number of favourable sequences of p A's and q B's is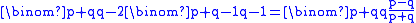
and thus the required probability is

as expected.
Variant: ties allowed
The original problem is to find the probability that the first candidate is always strictly ahead in the vote count. Consider now the problem to find the probability that the second candidate is never ahead (i.e. ties are allowed); the solution is .
.The variant problem can be solved by the reflection method in a similar way to the original problem. First note that the number of possible vote sequences is
 . Call a sequence "bad" if the second candidate is ever ahead, and if the number of bad sequences can be enumerated then the number of "good" sequences can be found by subtraction and the probability can be computed.
. Call a sequence "bad" if the second candidate is ever ahead, and if the number of bad sequences can be enumerated then the number of "good" sequences can be found by subtraction and the probability can be computed.Represent a voting sequence as a lattice path on the Cartesian plane as follows:
- Start the path at (0, 0)
- Each time a vote for the first candidate is received move right 1 unit.
- Each time a vote for the second candidate is received move up 1 unit.
Each such path corresponds to a unique sequence of votes and will end at (p, q). A sequence is 'good' exactly when the corresponding path never goes above the diagonal line y = x; equivalently, a sequence is 'bad' exactly when the corresponding path touches the line y = x + 1.

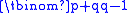 and so that is the number of 'bad' sequences. This leaves the number of 'good' sequences as
and so that is the number of 'bad' sequences. This leaves the number of 'good' sequences as
Since there are
 altogether, the probability of a sequence being good is
altogether, the probability of a sequence being good is 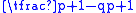 .
.In fact, the solutions to the original problem and the variant problem are easily related. For candidate A to be strictly ahead throughout the vote count, they must receive the first vote and for the remaining votes (ignoring the first) they must be either strictly ahead or tied throughout the count. Hence the solution to the original problem is
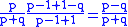
as required.

