Catalan number
Encyclopedia
In combinatorial mathematics
, the Catalan numbers form a sequence
of natural number
s that occur in various counting problems
, often involving
recursively
defined objects. They are named after the Belgian
mathematician
Eugène Charles Catalan
(1814–1894).
The nth Catalan number is given directly in terms of binomial coefficient
s by
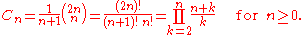
The first Catalan numbers for n = 0, 1, 2, 3, … are
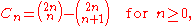
which is equivalent to the expression given above because
. This shows that Cn is a natural number
, which is not immediately obvious from the first formula given. This expression forms the basis for a proof of the correctness of the formula.
The Catalan numbers satisfy the recurrence relation
moreover,
This is due to the fact that :
since choosing n numbers from a 2n set of numbers can be uniquely divided into 2 parts by choosing i numbers of the first n numbers and then choosing n-i numbers (or i numbers) from the remaining n numbers.
They also satisfy:
which can be a more efficient way to calculate them.
Asymptotically, the Catalan numbers grow as
in the sense that the quotient of the nth Catalan number and the expression on the right tends towards
1 as n → +∞. (This can be proved by using Stirling's approximation
for n! .)
The only Catalan numbers Cn that are odd are those for which n = 2k − 1. All others are even.
whose solution is given by the Catalan numbers. The book Enumerative Combinatorics: Volume 2 by combinatorialist Richard P. Stanley
contains a set of exercises which describe 66 different interpretations of the Catalan numbers. Following are some examples, with illustrations of the cases C3 = 5 and C4 = 14.
If the leaves are labelled, we have the quadruple factorial numbers.
solves the combinatorial problems listed above. The first proof below uses a generating function
. The other proofs are examples of bijective proof
s; they involve literally counting a collection of some kind of object to arrive at the correct formula.
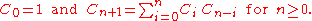
For example, every Dyck word w of length ≥ 2 can be written in a unique way in the form
with (possibly empty) Dyck words w1 and w2.
The generating function
for the Catalan numbers is defined by
The two recurrence relations together can then be summarized in generating function form by the relation
in other words, this equation follows from the recurrence relations by expanding both sides into power series. On the one hand, the recurrence relations uniquely determine the Catalan numbers; on the other hand, the generating function solution
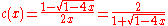
has a power series at 0 and its coefficients must therefore be the Catalan numbers. (Since the other solution has a pole at 0, this reasoning doesn't apply to it.)
The square root term can be expanded as a power series using the identity
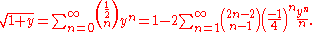
This is a special case of Newton's generalized binomial theorem; as with the general theorem, it can be proved by computing derivatives to produce its Taylor series. Setting y = −4x and substituting this power series into the expression for c(x) and shifting the summation index n by 1, the expansion simplifies to
The coefficients are now the desired formula for Cn.
Another way to get c(x) is to solve for xc(x) and observe that
appears in each term of the power series.
in complex analysis
), which was originally used in connection with Bertrand's ballot theorem. The reflection principle has been widely attributed to Désiré André, but his method did not actually use reflections; and the reflection method is a variation due to Aebly and Mirimanoff. It is most easily expressed in terms of the "monotonic paths which do not cross the diagonal" problem (see above).
Suppose we are given a monotonic path in an n × n grid that does cross the diagonal. Find the first edge in the path that lies above the diagonal, and flip the portion of the path occurring after that edge, along a line parallel to the diagonal. (In terms of Dyck words, we are starting with a sequence of n X's and n Y's which is not a Dyck word, and exchanging all X's with Y's after the first Y that violates the Dyck condition.) The resulting path is a monotonic path in an (n − 1) × (n + 1) grid. Figure 1 illustrates this procedure; the green portion of the path is the portion being flipped.
Since every monotonic path in the (n − 1) × (n + 1) grid must cross the diagonal at some point, every such path can be obtained in this fashion in precisely one way. The number of these paths is equal to
Therefore, to calculate the number of monotonic n × n paths which do not cross the diagonal, we need to subtract this from the total number of monotonic n × n paths, so we finally obtain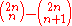
which is the nth Catalan number Cn.
Suppose we are given a monotonic path, which may happen to cross the diagonal. The exceedance of the path is defined to be the number of vertical edges which lie above the diagonal. For example, in Figure 2, the edges lying above the diagonal are marked in red, so the exceedance of the path is 5.
Now, if we are given a monotonic path whose exceedance is not zero, then we may apply the following algorithm to construct a new path whose exceedance is one less than the one we started with.
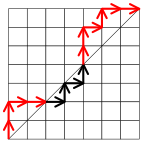
The following example should make this clearer. In Figure 3, the black dot indicates the point where the path first crosses the diagonal. The black edge is X, and we swap the red portion with the green portion to make a new path, shown in the second diagram.
Notice that the exceedance has dropped from three to two. In fact, the algorithm will cause the exceedance to decrease by one, for any path that we feed it, because the first vertical step starting on the diagonal (at the point marked with a black dot) is the unique vertical edge that under the operation passes from above the diagonal to below it; all other vertical edges stay on the same side of the diagonal.
It is also not difficult to see that this process is reversible: given any path P whose exceedance is less than n, there is exactly one path which yields P when the algorithm is applied to it. Indeed, the (black) edge X, which originally was the first horizontal step ending on the diagonal, has become the last horizontal step starting on the diagonal.
This implies that the number of paths of exceedance n is equal to the number of paths of exceedance n − 1, which is equal to the number of paths of exceedance n − 2, and so on, down to zero. In other words, we have split up the set of all monotonic paths into n + 1 equally sized classes, corresponding to the possible exceedances between 0 and n. Since there are
monotonic paths, we obtain the desired formula
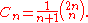
Figure 4 illustrates the situation for n = 3. Each of the 20 possible monotonic paths appears somewhere in the table. The first column shows all paths of exceedance three, which lie entirely above the diagonal. The columns to the right show the result of successive applications of the algorithm, with the exceedance decreasing one unit at a time. There are five rows, that is, C3 = 5.
The binomial formula for Cn follows immediately from this relation and the initial condition C1 = 1.
interpretation of the Catalan numbers, so Cn is the number of ways to correctly match n pairs of brackets. We denote a (possibly empty) correct string with c and its inverse (where "[" and "]" are exchanged) with c+. Since any c can be uniquely decomposed into c = [ c1 ] c2, summing over the possible spots to place the closing bracket immediately gives the recursive definition
Now let b stand for a balanced string of length 2n containing an equal number of "[" and "]" and
with some factor dn ≥ 1. As above, any balanced string can be uniquely decomposed into either [ c ] b or ] c+[b, so
Also, any incorrect balanced string starts with c ], so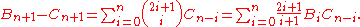
Subtracting the above equations and using Bi = di Ci gives
Comparing coefficients with the original recursion formula for Cn gives di = i + 1, so
1, regardless of the value of n. For example, for n = 4 we have
Note that if the entries are "shifted", namely the Catalan numbers Ci+j−1, the determinant is still 1, regardless of the size of n.
For example, for n = 4 we have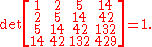
The Catalan numbers form the unique sequence with this property.
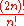, or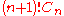 
. This is the solution to labelled variants of the above combinatorics problems. It is entirely distinct from the multifactorials.
, who was interested in the number of different ways of dividing a polygon into triangles. The sequence is named after Eugène Charles Catalan
, who discovered the connection to parenthesized expressions during his exploration of the Towers of Hanoi puzzle. The counting trick for Dyck words was found by D. André in 1887.
In 1988, it came to light in the Chinese publication Neimenggu Daxue Xuebao that the Catalan number sequence had been used in China
by the mathematician Antu Ming by 1730. That is when he started to write his book Ge Yuan Mi Lu Jie Fa, which was completed by his student Chen Jixin in 1774 but published sixty years later. P.J. Larcombe (1999) sketched some of the features of the work of Antu Ming, including the stimulus of Pierre Jartoux, who brought three infinite series to China early in the 1700s.
For instance, Ming used the Catalan sequence to express series expansions of sin(2α) and sin(4α) in terms of sin(α).
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
, the Catalan numbers form a sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
of natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s that occur in various counting problems
Enumeration
In mathematics and theoretical computer science, the broadest and most abstract definition of an enumeration of a set is an exact listing of all of its elements . The restrictions imposed on the type of list used depend on the branch of mathematics and the context in which one is working...
, often involving
recursively
Recursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
defined objects. They are named after the Belgian
Belgium
Belgium , officially the Kingdom of Belgium, is a federal state in Western Europe. It is a founding member of the European Union and hosts the EU's headquarters, and those of several other major international organisations such as NATO.Belgium is also a member of, or affiliated to, many...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Eugène Charles Catalan
Eugène Charles Catalan
Eugène Charles Catalan was a French and Belgian mathematician.- Biography :Catalan was born in Bruges , the only child of a French jeweller by the name of Joseph Catalan, in 1814. In 1825, he traveled to Paris and learned mathematics at École Polytechnique, where he met Joseph Liouville...
(1814–1894).
The nth Catalan number is given directly in terms of binomial coefficient
Binomial coefficient
In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
s by
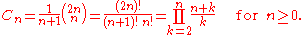
The first Catalan numbers for n = 0, 1, 2, 3, … are
- 1, 1, 2, 5, 1414 (number)14 is the natural number following 13 and preceding 15.In speech, the numbers 14 and 40 are often confused. When carefully enunciated, they differ in which syllable is stressed: 14 vs 40...
, 4242 (number)42 is the natural number immediately following 41 and directly preceding 43. The number has received considerable attention in popular culture as a result of its central appearance in The Hitchhiker's Guide to the Galaxy as the "Answer to the Ultimate Question of Life, the Universe, and...
, 132132 (number)132 is the natural number following 131 and preceding 133.-In mathematics:132 is the sixth Catalan number. It is a pronic number, the product of 11 and 12. As it has 12 divisors total, 132 is a refactorable number....
, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452, …
Properties
An alternative expression for Cn is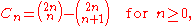which is equivalent to the expression given above because
. This shows that Cn is a natural numberNatural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
, which is not immediately obvious from the first formula given. This expression forms the basis for a proof of the correctness of the formula.
The Catalan numbers satisfy the recurrence relation
Recurrence relation
In mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....
moreover,
This is due to the fact that :
since choosing n numbers from a 2n set of numbers can be uniquely divided into 2 parts by choosing i numbers of the first n numbers and then choosing n-i numbers (or i numbers) from the remaining n numbers.They also satisfy:
which can be a more efficient way to calculate them.
Asymptotically, the Catalan numbers grow as
in the sense that the quotient of the nth Catalan number and the expression on the right tends towards
Limit of a function
In mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input....
1 as n → +∞. (This can be proved by using Stirling's approximation
Stirling's approximation
In mathematics, Stirling's approximation is an approximation for large factorials. It is named after James Stirling.The formula as typically used in applications is\ln n! = n\ln n - n +O\...
for n
The only Catalan numbers Cn that are odd are those for which n = 2k − 1. All others are even.
Applications in combinatorics
There are many counting problems in combinatoricsCombinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
whose solution is given by the Catalan numbers. The book Enumerative Combinatorics: Volume 2 by combinatorialist Richard P. Stanley
Richard P. Stanley
Richard Peter Stanley is the Norman Levinson Professor of Applied Mathematics at the Massachusetts Institute of Technology, in Cambridge, Massachusetts. He received his Ph.D. at Harvard University in 1971 under the supervision of Gian-Carlo Rota...
contains a set of exercises which describe 66 different interpretations of the Catalan numbers. Following are some examples, with illustrations of the cases C3 = 5 and C4 = 14.
- Cn is the number of Dyck words of length 2n. A Dyck word is a stringString (computer science)In formal languages, which are used in mathematical logic and theoretical computer science, a string is a finite sequence of symbols that are chosen from a set or alphabet....
consisting of n X's and n Y's such that no initial segment of the string has more Y's than X's (see also Dyck languageDyck languageIn the theory of formal languages of computer science, mathematics, and linguistics, the Dyck language is the language consisting of balanced strings of parentheses [ and ]. It is important in the parsing of expressions that must have a correctly nested sequence of parentheses, such as arithmetic...
). For example, the following are the Dyck words of length 6:
- Re-interpreting the symbol X as an open parenthesis and Y as a close parenthesis, Cn counts the number of expressions containing n pairs of parentheses which are correctly matched:
- Cn is the number of different ways n + 1 factors can be completely parenthesizedBracketBrackets are tall punctuation marks used in matched pairs within text, to set apart or interject other text. In the United States, "bracket" usually refers specifically to the "square" or "box" type.-List of types:...
(or the number of ways of associatingAssociativityIn mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...
n applications of a binary operator). For n = 3, for example, we have the following five different parenthesizations of four factors:
- Successive applications of a binary operator can be represented in terms of a full binary treeBinary treeIn computer science, a binary tree is a tree data structure in which each node has at most two child nodes, usually distinguished as "left" and "right". Nodes with children are parent nodes, and child nodes may contain references to their parents. Outside the tree, there is often a reference to...
. (A rooted binary tree is full if every vertex has either two children or no children.) It follows that Cn is the number of full binary treesTree (graph theory)In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...
with n + 1 leaves:
If the leaves are labelled, we have the quadruple factorial numbers.
- Cn is the number of non-isomorphic ordered trees with n+1 vertices. (An ordered tree is a rooted tree in which the children of each vertex are given a fixed left-to-right order.)
- Cn is the number of monotonic paths along the edges of a grid with n × n square cells, which do not pass above the diagonal. A monotonic path is one which starts in the lower left corner, finishes in the upper right corner, and consists entirely of edges pointing rightwards or upwards. Counting such paths is equivalent to counting Dyck words: X stands for "move right" and Y stands for "move up". The following diagrams show the case n = 4:
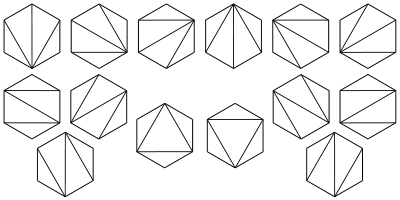
- Cn is the number of different ways a convex polygonConvex polygonIn geometry, a polygon can be either convex or concave .- Convex polygons :A convex polygon is a simple polygon whose interior is a convex set...
with n + 2 sides can be cut into triangleTriangleA triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
s by connecting vertices with straight lines. The following hexagons illustrate the case n = 4:
- Cn is the number of stackStack (data structure)In computer science, a stack is a last in, first out abstract data type and linear data structure. A stack can have any abstract data type as an element, but is characterized by only three fundamental operations: push, pop and stack top. The push operation adds a new item to the top of the stack,...
-sortable permutationPermutationIn mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
s of {1, ..., n}. A permutation w is called stack-sortable if S(w) = (1, ..., n), where S(w) is defined recursively as follows: write w = unv where n is the largest element in w and u and v are shorter sequences, and set S(w) = S(u)S(v)n, with S being the identity for one-element sequences. These are the permutations that avoid the patternPermutation patternIn combinatorial mathematics and theoretical computer science, a permutation pattern is a sub-permutation of a longer permutation. The permutation π, written as a word in one-line notation , is said to contain the permutation σ if there exists a subsequence of entries of π that has the same...
231.
- Cn is the number of permutations of {1, ..., n} that avoid the pattern 123 (or any of the other patterns of length 3); that is, the number of permutations with no three-term increasing subsequence. For n = 3, these permutations are 132, 213, 231, 312 and 321. For n = 4, they are 1432, 2143, 2413, 2431, 3142, 3214, 3241, 3412, 3421, 4132, 4213, 4231, 4312 and 4321.
- Cn is the number of noncrossing partitionNoncrossing partitionIn combinatorial mathematics, the topic of noncrossing partitions has assumed some importance because of its application to the theory of free probability...
s of the set {1, ..., n}. A fortioriA fortiori argumentThe Latin phrase ' denotes "argument 'from [the] stronger [reason]'." For example, if it has been established that a person is deceased, then one can, with equal or greater certainty, argue that the person is not breathing.-Usage:...
, Cn never exceeds the nth Bell numberBell numberIn combinatorics, the nth Bell number, named after Eric Temple Bell, is the number of partitions of a set with n members, or equivalently, the number of equivalence relations on it...
. Cn is also the number of noncrossing partitions of the set {1, ..., 2n} in which every block is of size 2. The conjunction of these two facts may be used in a proof by mathematical inductionMathematical inductionMathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
that all of the free cumulantCumulantIn probability theory and statistics, the cumulants κn of a probability distribution are a set of quantities that provide an alternative to the moments of the distribution. The moments determine the cumulants in the sense that any two probability distributions whose moments are identical will have...
s of degree more than 2 of the Wigner semicircle law are zero. This law is important in free probabilityFree probabilityFree probability is a mathematical theory that studies non-commutative random variables. The "freeness" or free independence property is the analogue of the classical notion of independence, and it is connected with free products....
theory and the theory of random matrices.
- Cn is the number of ways to tile a stairstep shape of height n with n rectangles. The following figure illustrates the case n = 4:
- Cn is the number of standard Young tableaux whose diagram is a 2-by-n rectangle. In other words, it is the number ways the numbers 1, 2, ..., 2n can be arranged in a 2-by-n rectangle so that each row and each column is increasing. As such, the formula can be derived as a special case of the hook-length formula.
- Cn is the number of ways that the vertices of a convex 2n-gon can be paired so that the line segments joining paired vertices do not intersect.
- Cn is the number of semiorderSemiorderIn order theory, a branch of mathematics, a semiorder is a type of ordering that may be determined for a set of items with numerical scores by declaring two items to be incomparable when their scores are within some threshold of each other and otherwise using the numerical comparison of their scores...
s on n unlabeled items.
Proof of the formula
There are several ways of explaining why the formulasolves the combinatorial problems listed above. The first proof below uses a generating function
Generating function
In mathematics, a generating function is a formal power series in one indeterminate, whose coefficients encode information about a sequence of numbers an that is indexed by the natural numbers. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general...
. The other proofs are examples of bijective proof
Bijective proof
In combinatorics, bijective proof is a proof technique that finds a bijective function f : A → B between two sets A and B, thus proving that they have the same number of elements, |A| = |B|. One place the technique is useful is where we wish to know the size of A, but can find no direct way of...
s; they involve literally counting a collection of some kind of object to arrive at the correct formula.
First proof
We first observe that all of the combinatorial problems listed above satisfy Segner's recurrence relationRecurrence relation
In mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....
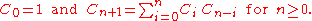
For example, every Dyck word w of length ≥ 2 can be written in a unique way in the form
- w = Xw1Yw2
with (possibly empty) Dyck words w1 and w2.
The generating function
Generating function
In mathematics, a generating function is a formal power series in one indeterminate, whose coefficients encode information about a sequence of numbers an that is indexed by the natural numbers. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general...
for the Catalan numbers is defined by
The two recurrence relations together can then be summarized in generating function form by the relation
in other words, this equation follows from the recurrence relations by expanding both sides into power series. On the one hand, the recurrence relations uniquely determine the Catalan numbers; on the other hand, the generating function solution
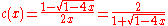
has a power series at 0 and its coefficients must therefore be the Catalan numbers. (Since the other solution has a pole at 0, this reasoning doesn't apply to it.)
The square root term can be expanded as a power series using the identity
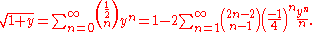
This is a special case of Newton's generalized binomial theorem; as with the general theorem, it can be proved by computing derivatives to produce its Taylor series. Setting y = −4x and substituting this power series into the expression for c(x) and shifting the summation index n by 1, the expansion simplifies to
The coefficients are now the desired formula for Cn.
Another way to get c(x) is to solve for xc(x) and observe that
appears in each term of the power series.Second proof
This proof depends on a trick known as André's reflection method (not to be confused with the Schwarz reflection principleSchwarz reflection principle
This article is about the reflection principle in complex analysis. For the reflection principles of set theory, see Reflection principleIn mathematics, the Schwarz reflection principle is a way to extend the domain of definition of an analytic function of a complex variable F, which is defined on...
in complex analysis
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
), which was originally used in connection with Bertrand's ballot theorem. The reflection principle has been widely attributed to Désiré André, but his method did not actually use reflections; and the reflection method is a variation due to Aebly and Mirimanoff. It is most easily expressed in terms of the "monotonic paths which do not cross the diagonal" problem (see above).
Since every monotonic path in the (n − 1) × (n + 1) grid must cross the diagonal at some point, every such path can be obtained in this fashion in precisely one way. The number of these paths is equal to
Therefore, to calculate the number of monotonic n × n paths which do not cross the diagonal, we need to subtract this from the total number of monotonic n × n paths, so we finally obtain
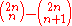
which is the nth Catalan number Cn.
Third proof
The following bijective proof, while being more involved than the previous one, provides a more natural explanation for the term n + 1 appearing in the denominator of the formula for Cn.Now, if we are given a monotonic path whose exceedance is not zero, then we may apply the following algorithm to construct a new path whose exceedance is one less than the one we started with.
- Starting from the bottom left, follow the path until it first travels above the diagonal.
- Continue to follow the path until it touches the diagonal again. Denote by X the first such edge that is reached.
- Swap the portion of the path occurring before X with the portion occurring after X.
The following example should make this clearer. In Figure 3, the black dot indicates the point where the path first crosses the diagonal. The black edge is X, and we swap the red portion with the green portion to make a new path, shown in the second diagram.
This implies that the number of paths of exceedance n is equal to the number of paths of exceedance n − 1, which is equal to the number of paths of exceedance n − 2, and so on, down to zero. In other words, we have split up the set of all monotonic paths into n + 1 equally sized classes, corresponding to the possible exceedances between 0 and n. Since there are
monotonic paths, we obtain the desired formula
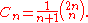
Figure 4 illustrates the situation for n = 3. Each of the 20 possible monotonic paths appears somewhere in the table. The first column shows all paths of exceedance three, which lie entirely above the diagonal. The columns to the right show the result of successive applications of the algorithm, with the exceedance decreasing one unit at a time. There are five rows, that is, C3 = 5.
Fourth proof
This proof uses the triangulation definition of Catalan numbers to establish a relation between Cn and Cn+1. Given a polygon P with n+ 2 sides, first mark one of its sides as the base. If P is then triangulated, we can further choose and orient one of its 2n+1 edges. There are (4n+2)Cn such decorated triangulations. Now given a polygon Q with n+3 sides, again mark one of its sides as the base. If Q is triangulated, we can further mark one of the sides other than the base side. There are (n+2)Cn+1 such decorated triangulations. Then there is a simple bijection between these two kinds of decorated triangulations: We can either collapse the triangle in Q whose side is marked, or in reverse expand the oriented edge in P to a triangle and mark its new side. ThusThe binomial formula for Cn follows immediately from this relation and the initial condition C1 = 1.
Fifth proof
This proof is based on the Dyck wordsDyck language
In the theory of formal languages of computer science, mathematics, and linguistics, the Dyck language is the language consisting of balanced strings of parentheses [ and ]. It is important in the parsing of expressions that must have a correctly nested sequence of parentheses, such as arithmetic...
interpretation of the Catalan numbers, so Cn is the number of ways to correctly match n pairs of brackets. We denote a (possibly empty) correct string with c and its inverse (where "[" and "]" are exchanged) with c+. Since any c can be uniquely decomposed into c = [ c1 ] c2, summing over the possible spots to place the closing bracket immediately gives the recursive definition
Now let b stand for a balanced string of length 2n containing an equal number of "[" and "]" and
with some factor dn ≥ 1. As above, any balanced string can be uniquely decomposed into either [ c ] b or ] c+[b, soAlso, any incorrect balanced string starts with c ], so
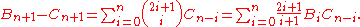
Subtracting the above equations and using Bi = di Ci gives
Comparing coefficients with the original recursion formula for Cn gives di = i + 1, so
Hankel matrix
The n×n Hankel matrix whose (i, j) entry is the Catalan number Ci+j−2 has determinantDeterminant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
1, regardless of the value of n. For example, for n = 4 we have
Note that if the entries are "shifted", namely the Catalan numbers Ci+j−1, the determinant is still 1, regardless of the size of n.
For example, for n = 4 we have
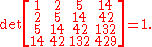
The Catalan numbers form the unique sequence with this property.
Quadruple factorial
The quadruple factorial is given by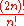, or 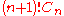. This is the solution to labelled variants of the above combinatorics problems. It is entirely distinct from the multifactorials.History
The Catalan sequence was first described in the 18th century by Leonhard EulerLeonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
, who was interested in the number of different ways of dividing a polygon into triangles. The sequence is named after Eugène Charles Catalan
Eugène Charles Catalan
Eugène Charles Catalan was a French and Belgian mathematician.- Biography :Catalan was born in Bruges , the only child of a French jeweller by the name of Joseph Catalan, in 1814. In 1825, he traveled to Paris and learned mathematics at École Polytechnique, where he met Joseph Liouville...
, who discovered the connection to parenthesized expressions during his exploration of the Towers of Hanoi puzzle. The counting trick for Dyck words was found by D. André in 1887.
In 1988, it came to light in the Chinese publication Neimenggu Daxue Xuebao that the Catalan number sequence had been used in China
China
Chinese civilization may refer to:* China for more general discussion of the country.* Chinese culture* Greater China, the transnational community of ethnic Chinese.* History of China* Sinosphere, the area historically affected by Chinese culture...
by the mathematician Antu Ming by 1730. That is when he started to write his book Ge Yuan Mi Lu Jie Fa, which was completed by his student Chen Jixin in 1774 but published sixty years later. P.J. Larcombe (1999) sketched some of the features of the work of Antu Ming, including the stimulus of Pierre Jartoux, who brought three infinite series to China early in the 1700s.
For instance, Ming used the Catalan sequence to express series expansions of sin(2α) and sin(4α) in terms of sin(α).
See also
- AssociahedronAssociahedronIn mathematics, an associahedron or Stasheff polytope Kn is a convex polytope in which each vertex corresponds to a way of correctly inserting opening and closing parentheses in a word of n letters and the edges correspond to single application of the associativity rule.Initially Jim Stasheff...
- Bertrand's ballot theorem
- Binomial transform
- Catalan's problemCatalan's problemIn mathematics, Catalan's problem asks the number of ways n + 1 factors can be completely parenthesized by n pairs of parentheses...
- Catalan–Mersenne number
- List of factorial and binomial topics
- Lobb numbersLobb numbersThe Lobb numbers, named after Andrew Lobb, are a natural generalization of the Catalan numbers, originally introduced to give a simple inductive proof of the formula for the nth Catalan number....
- Narayana numberNarayana numberIn combinatorics, the Narayana numbers N, n = 1, 2, 3 ..., 1 ≤ k ≤ n, form a triangular array of natural numbers, called Narayana triangle, that occur in various counting problems. They are named for T.V...
- Tamari latticeTamari latticeIn mathematics, a Tamari lattice, introduced by , is a partially ordered set in which the elements consist of different ways of grouping a sequence of objects into pairs using parentheses; for instance, for a sequence of four objects abcd, the five possible groupings are d, , d, a, and a...
External links
- Dickau, Robert M.: Catalan numbers Further examples.
- Davis, Tom: Catalan numbers. Still more examples.
- Schmidthammer, Jürgen: Catalan-Zahlen Zulassungsarbeit zum Staatsexamen (PDF-File; 7,05 MB)
- "Equivalence of Three Catalan Number Interpretations" from The Wolfram Demonstrations Project http://demonstrations.wolfram.com/EquivalenceOfThreeCatalanNumberInterpretations/