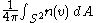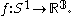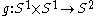Average crossing number
Encyclopedia
In the mathematical
subject of knot theory
, the average crossing number of a knot
is the result of averaging over all directions the number of crossings
in a knot diagram of the knot obtained by projection onto the plane orthogonal to the direction. The average crossing number is often seen in the context of physical knot theory
.
More precisely, if K is a smooth knot, then for almost every unit vector v giving the direction, orthogonal projection onto the plane perpendicular to v gives a knot diagram, and we can compute the crossing number, denoted n(v). The average crossing number is then defined as the integral over the unit sphere:
where dA is the area form on the 2-sphere. The integral makes sense because the set of directions where projection doesn't give a knot diagram is a set of measure zero and n(v) is locally constant when defined.
A less intuitive but computationally useful definition is an integral
similar to the Gauss linking integral.
We will give a derivation analogous to the derivation of the linking integral. Let K be a knot, parametrized by
Then define the map from the torus
to the 2-sphere
by
(Technically, we need to avoid the diagonal: points where s = t .) We want to count the number of times a point (direction) is covered by g. This will count, for a generic direction, the number of crossings in a knot diagram given by projecting along that direction. Using the degree of the map, as in the linking integral, would count the number of crossings with sign, giving the writhe
. Use g to pullback the area form on S2 to the torus T2 = S1 × S1. Instead of integrating this form, we integrate the absolute value of it, to avoid the sign issue. The resulting integral is
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
subject of knot theory
Knot theory
In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...
, the average crossing number of a knot
Knot (mathematics)
In mathematics, a knot is an embedding of a circle in 3-dimensional Euclidean space, R3, considered up to continuous deformations . A crucial difference between the standard mathematical and conventional notions of a knot is that mathematical knots are closed—there are no ends to tie or untie on a...
is the result of averaging over all directions the number of crossings
Crossing number (knot theory)
In the mathematical area of knot theory, the crossing number of a knot is the minimal number of crossings of any diagram of the knot. It is a knot invariant....
in a knot diagram of the knot obtained by projection onto the plane orthogonal to the direction. The average crossing number is often seen in the context of physical knot theory
Physical knot theory
Physical knot theory is the study of mathematical models of knotting phenomena, often motivated by physical considerations from biology, chemistry, and physics. Traditional knot theory models a knot as a simple closed loop in three dimensional space. Such a knot has no thickness or physical...
.
More precisely, if K is a smooth knot, then for almost every unit vector v giving the direction, orthogonal projection onto the plane perpendicular to v gives a knot diagram, and we can compute the crossing number, denoted n(v). The average crossing number is then defined as the integral over the unit sphere:
where dA is the area form on the 2-sphere. The integral makes sense because the set of directions where projection doesn't give a knot diagram is a set of measure zero and n(v) is locally constant when defined.
A less intuitive but computationally useful definition is an integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
similar to the Gauss linking integral.
We will give a derivation analogous to the derivation of the linking integral. Let K be a knot, parametrized by
Then define the map from the torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
to the 2-sphere
by
(Technically, we need to avoid the diagonal: points where s = t .) We want to count the number of times a point (direction) is covered by g. This will count, for a generic direction, the number of crossings in a knot diagram given by projecting along that direction. Using the degree of the map, as in the linking integral, would count the number of crossings with sign, giving the writhe
Writhe
In knot theory, the writhe is a property of an oriented link diagram. The writhe is the total number of positive crossings minus the total number of negative crossings....
. Use g to pullback the area form on S2 to the torus T2 = S1 × S1. Instead of integrating this form, we integrate the absolute value of it, to avoid the sign issue. The resulting integral is