
Abbott-Firestone curve
Encyclopedia
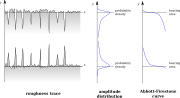
Mathematically it is the cumulative probability density function
Cumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
of the surface profile's height and can be calculated by integrating the profile trace.
The Abbott-Firestone was first described by EJ Abbott and FA Firestone in 1933. It is useful for understanding the properties of sealing and bearing surfaces. It is commonly used in the engineering and manufacturing piston cylinder bores of internal combustion engines. The shape of the curve is distilled into several of the surface roughness parameters, especially the Rk family of parameters.

