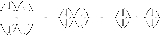
2-category
Encyclopedia
In category theory
, a 2-category is a category
with "morphisms between morphisms"; that is, where each hom set
itself carries the structure of a category. It can be formally defined as a category enriched
over Cat (the category of categories and functors, with the monoidal
structure given by product of categories
).
The notion of 2-category differs from the more general notion of a bicategory
in that composition of 1-cells (horizontal composition) is required to be strictly associative, whereas in a bicategory it need only be associative up to a 2-isomorphism. The axioms of a 2-category are consequences of their definition as Cat-enriched categories:
The interchange law follows from the fact that
is a functor between hom categories. It can be drawn as a pasting diagram as follows:
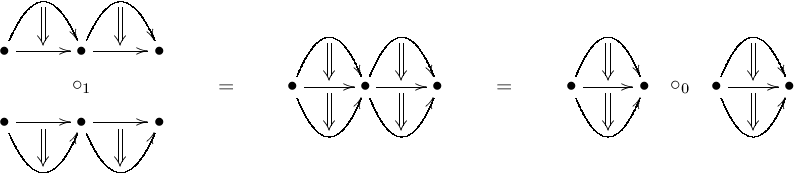
Here the left-hand diagram denotes the vertical composition of horizontal composites, the right-hand diagram denotes the horizontal composition of vertical composites, and the diagram in the centre is the customary representation of both.
, as invented by Lawvere, is an example of a doctrine, as are multi-sorted theories, operads, categories
, and toposes.
The objects of the 2-category are called theories, the 1-morphisms
are called models of the 
in 
, and the 2-morphisms are called morphisms between models.
The distinction between a 2-category and a doctrine is really only heuristic: one does not typically consider a 2-category to be populated by theories as objects and models as morphisms. It is this vocabulary that makes the theory of doctrines worth while.
For example, the 2-category Cat of categories, functors, and natural transformations is a doctrine. One sees immediately that all presheaf categories are categories of models.
As another example, one may take the subcategory of Cat consisting only of categories with finite products as objects and product-preserving functors as 1-morphisms. This is the doctrine of multi-sorted algebraic theories. If one only wanted 1-sorted algebraic theories, one would restrict the objects to only those categories that are generated under products by a single object.
Doctrines were invented by J. M. Beck.
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, a 2-category is a category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
with "morphisms between morphisms"; that is, where each hom set
Morphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
itself carries the structure of a category. It can be formally defined as a category enriched
Enriched category
In category theory and its applications to mathematics, enriched category is a generalization of category that abstracts the set of morphisms associated with every pair of objects to an opaque object in some fixed monoidal category of "hom-objects" and then defines composition and identity solely...
over Cat (the category of categories and functors, with the monoidal
Monoidal category
In mathematics, a monoidal category is a category C equipped with a bifunctorwhich is associative, up to a natural isomorphism, and an object I which is both a left and right identity for ⊗, again up to a natural isomorphism...
structure given by product of categories
Product category
In the mathematical field of category theory, the product of two categories C and D, denoted and called a product category, is a straightforward extension of the concept of the Cartesian product of two sets.-Definition:...
).
Definition
A 2-category C consists of:- A class of 0-cells (or objects) A, B, ....
- For all objects A and B, a category
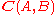. The objects 
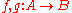of this category are called 1-cells and its morphisms 
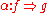are called 2-cells; the composition in this category is usually written 
or 
and called vertical composition or composition along a 1-cell.
- For any object A there is a functor from the terminal category (with one object and one arrow) to
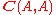, that picks out the identity 1-cell idA on A and its identity 2-cell ididA. In practice these two are often denoted simply by A.
- For all objects A, B and C, there is a functor
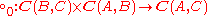, called horizontal composition or composition along a 0-cell, which is associative and admits the identity 2-cells of idA as identities. The composition symbol 
is often omitted, the horizontal composite of 2-cells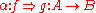 
and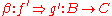 
being written simply as 
.
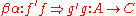The notion of 2-category differs from the more general notion of a bicategory
Bicategory
In mathematics, a bicategory is a concept in category theory used to extend the notion of category to handle the cases where the composition of morphisms is not associative, but only associative up to an isomorphism. The notion was introduced in 1967 by Jean Bénabou.Formally, a bicategory B...
in that composition of 1-cells (horizontal composition) is required to be strictly associative, whereas in a bicategory it need only be associative up to a 2-isomorphism. The axioms of a 2-category are consequences of their definition as Cat-enriched categories:
- Vertical composition is associative and unital, the units being the identity 2-cells
. - Horizontal composition is also (strictly) associative and unital, the units being the identity 2-cells
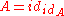on the identity 1-cells 
. - The interchange law holds; i.e. it is true that for composable 2-cells
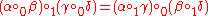
The interchange law follows from the fact that
is a functor between hom categories. It can be drawn as a pasting diagram as follows:Here the left-hand diagram denotes the vertical composition of horizontal composites, the right-hand diagram denotes the horizontal composition of vertical composites, and the diagram in the centre is the customary representation of both.
Doctrines
In mathematics, a doctrine is simply a 2-category which is heuristically regarded as a system of theories. For example, algebraic theoriesAlgebraic theory
In mathematical logic, an algebraic theory is one that uses axioms stated entirely in terms of equations between terms with free variables. Inequalities and quantifiers are specifically disallowed. Sentential logic is the subset of first-order logic involving only algebraic sentences.Saying that...
, as invented by Lawvere, is an example of a doctrine, as are multi-sorted theories, operads, categories
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
, and toposes.
The objects of the 2-category are called theories, the 1-morphisms
are called models of the in , and the 2-morphisms are called morphisms between models.The distinction between a 2-category and a doctrine is really only heuristic: one does not typically consider a 2-category to be populated by theories as objects and models as morphisms. It is this vocabulary that makes the theory of doctrines worth while.
For example, the 2-category Cat of categories, functors, and natural transformations is a doctrine. One sees immediately that all presheaf categories are categories of models.
As another example, one may take the subcategory of Cat consisting only of categories with finite products as objects and product-preserving functors as 1-morphisms. This is the doctrine of multi-sorted algebraic theories. If one only wanted 1-sorted algebraic theories, one would restrict the objects to only those categories that are generated under products by a single object.
Doctrines were invented by J. M. Beck.