
Kummer surface
Encyclopedia
In algebraic geometry
, a Kummer quartic surface, first studied by , is an irreducible algebraic surface
of degree 4 in with the maximal possible number of 16 double points. Any such surface is the Kummer variety
with the maximal possible number of 16 double points. Any such surface is the Kummer variety
of the Jacobian
of a smooth hyperelliptic curve of genus
2; i.e. a quotient of the Jacobian by the Kummer involution x ↦ −x. The Kummer involution has 16 fixed points: the 16 2-torsion point of the Jacobian, and they are the 16 singular points of the quartic surface.
Resolving the 16 double points of the quotient of a (possibly nonalgebraic) torus by the Kummer involution gives a K3 surface
with 16 disjoint rational curves; these K3 surfaces are also sometimes called Kummer surfaces.
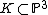 be a quartic surface, and let p be a singular point of this surface. Identifying the lines in
be a quartic surface, and let p be a singular point of this surface. Identifying the lines in  through the point p with
through the point p with 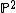 , we get a double cover from the blow up of K at p to
, we get a double cover from the blow up of K at p to 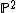 ; this double cover is given by
; this double cover is given by
sending q ≠ p ↦ , and any line in the tangent cone
, and any line in the tangent cone
of p in K to itself. The ramification locus of the double cover is a plane curve C of degree 6, and all the nodes of K which are not p map to nodes of C.
By the genus degree formula, the maximal number possible number of nodes on a sextic curve is obtained when the curve is a union of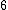 lines, in which case we have 15 nodes. Hence the maximal number of nodes on a quartic is 16, and in this case they are all simple nodes (to show that
lines, in which case we have 15 nodes. Hence the maximal number of nodes on a quartic is 16, and in this case they are all simple nodes (to show that 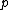 is simple project from another node). A quartic which obtains these 16 nodes is called a Kummer Quartic, and we will concentrate on them below.
is simple project from another node). A quartic which obtains these 16 nodes is called a Kummer Quartic, and we will concentrate on them below.
Since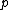 is a simple node, the tangent cone to this point is mapped to a conic under the double cover. This conic is in fact tangent to the six lines (w.o proof). Conversely, given a configuration of a conic and six lines which tangent to it in the plane, we may define the double cover of the plane ramified over the union of these 6 lines. This double cover may be mapped to
is a simple node, the tangent cone to this point is mapped to a conic under the double cover. This conic is in fact tangent to the six lines (w.o proof). Conversely, given a configuration of a conic and six lines which tangent to it in the plane, we may define the double cover of the plane ramified over the union of these 6 lines. This double cover may be mapped to  , under a map which blows down the double cover of the special conic, and is an isomorphism elsewhere (w.o. proof).
, under a map which blows down the double cover of the special conic, and is an isomorphism elsewhere (w.o. proof).
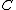 of genus 2, we may identify the Jacobian
of genus 2, we may identify the Jacobian 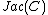
with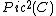 under the map
under the map 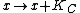 . We now observe two facts: Since
. We now observe two facts: Since 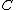 is a hyperelliptic curve the map from the symmetric product
is a hyperelliptic curve the map from the symmetric product
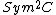 to
to  , defined by
, defined by  , is the blow down of the diagonal to the canonical divisor class. Moreover, the canonical map
, is the blow down of the diagonal to the canonical divisor class. Moreover, the canonical map  is a double cover. Hence we get a double cover
is a double cover. Hence we get a double cover  .
.
This double cover is the one which already appeared above: The 6 lines are the images of the odd symmetric theta divisors on , while the conic is the image of the blown-up 0. The conic is isomorphic to the canonical system via the isomorphism
, while the conic is the image of the blown-up 0. The conic is isomorphic to the canonical system via the isomorphism  , and each of the six lines is naturally isomorphic to the dual canonical system
, and each of the six lines is naturally isomorphic to the dual canonical system 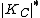 via the identification of theta divisors and translates of the curve
via the identification of theta divisors and translates of the curve  . There is a 1-1 correspondence between pairs of odd symmetric theta divisors and 2-torsion points on the Jacobian given by the fact that
. There is a 1-1 correspondence between pairs of odd symmetric theta divisors and 2-torsion points on the Jacobian given by the fact that 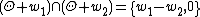 , where
, where  are Weierstrass points (which are the odd theta characteristics in this in genus 2). Hence the branch points of the canonical map
are Weierstrass points (which are the odd theta characteristics in this in genus 2). Hence the branch points of the canonical map 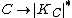 appear on each of these copies of the canonical system as the intersection points of the lines and the tangency points of the lines and the conic.
appear on each of these copies of the canonical system as the intersection points of the lines and the tangency points of the lines and the conic.
Finally, since we know that every Kummer quartic is a Kummer variety of a Jacobian of a hyperelliptic curve, we show how to reconstruct Kummer quartic surface directly from the Jacobian of a genus 2 curve: The Jacobian of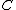 maps to the complete linear system
maps to the complete linear system
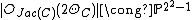 (see the article on Abelian varieties
(see the article on Abelian varieties
). This maps factors through the Kummer variety as a degree 4 map which has 16 nodes at the images of the 2-torsion points on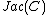 .
.
Kummer's
There are several crucial points which relate the geometric, algebraic, and combinatorial aspects of the configuration of the nodes of the kummer quartic:
Hence we have a configuration of conics in
conics in 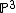 ; where each contains 6 nodes, and such that the intersection of each two is along 2 nodes. This configuration is called the
; where each contains 6 nodes, and such that the intersection of each two is along 2 nodes. This configuration is called the 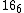 configuration.
configuration.
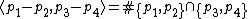 . One can recover a lot of the group theoretic invariants of the group
. One can recover a lot of the group theoretic invariants of the group 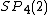 via the geometry of the
via the geometry of the  configuration.
configuration.
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, a Kummer quartic surface, first studied by , is an irreducible algebraic surface
Algebraic surface
In mathematics, an algebraic surface is an algebraic variety of dimension two. In the case of geometry over the field of complex numbers, an algebraic surface has complex dimension two and so of dimension four as a smooth manifold.The theory of algebraic surfaces is much more complicated than that...
of degree 4 in
 with the maximal possible number of 16 double points. Any such surface is the Kummer variety
with the maximal possible number of 16 double points. Any such surface is the Kummer varietyKummer variety
In mathematics, the Kummer variety of an abelian variety is its quotient by the map taking any element to its inverse.The Kummer variety of a 2-dimensional abelian variety is called a Kummer surface....
of the Jacobian
Jacobian
In vector calculus, the Jacobian matrix is the matrix of all first-order partial derivatives of a vector- or scalar-valued function with respect to another vector. Suppose F : Rn → Rm is a function from Euclidean n-space to Euclidean m-space...
of a smooth hyperelliptic curve of genus
Genus (mathematics)
In mathematics, genus has a few different, but closely related, meanings:-Orientable surface:The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It...
2; i.e. a quotient of the Jacobian by the Kummer involution x ↦ −x. The Kummer involution has 16 fixed points: the 16 2-torsion point of the Jacobian, and they are the 16 singular points of the quartic surface.
Resolving the 16 double points of the quotient of a (possibly nonalgebraic) torus by the Kummer involution gives a K3 surface
K3 surface
In mathematics, a K3 surface is a complex or algebraic smooth minimal complete surface that is regular and has trivial canonical bundle.In the Enriques-Kodaira classification of surfaces they form one of the 5 classes of surfaces of Kodaira dimension 0....
with 16 disjoint rational curves; these K3 surfaces are also sometimes called Kummer surfaces.
Singular quartic surfaces and the double plane model
Let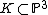 be a quartic surface, and let p be a singular point of this surface. Identifying the lines in
be a quartic surface, and let p be a singular point of this surface. Identifying the lines in  through the point p with
through the point p with 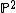 , we get a double cover from the blow up of K at p to
, we get a double cover from the blow up of K at p to 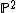 ; this double cover is given by
; this double cover is given bysending q ≠ p ↦
 , and any line in the tangent cone
, and any line in the tangent coneTangent cone
In geometry, the tangent cone is a generalization of the notion of the tangent space to a manifold to the case of certain spaces with singularities.- Definition in convex geometry :...
of p in K to itself. The ramification locus of the double cover is a plane curve C of degree 6, and all the nodes of K which are not p map to nodes of C.
By the genus degree formula, the maximal number possible number of nodes on a sextic curve is obtained when the curve is a union of
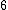 lines, in which case we have 15 nodes. Hence the maximal number of nodes on a quartic is 16, and in this case they are all simple nodes (to show that
lines, in which case we have 15 nodes. Hence the maximal number of nodes on a quartic is 16, and in this case they are all simple nodes (to show that 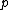 is simple project from another node). A quartic which obtains these 16 nodes is called a Kummer Quartic, and we will concentrate on them below.
is simple project from another node). A quartic which obtains these 16 nodes is called a Kummer Quartic, and we will concentrate on them below.Since
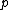 is a simple node, the tangent cone to this point is mapped to a conic under the double cover. This conic is in fact tangent to the six lines (w.o proof). Conversely, given a configuration of a conic and six lines which tangent to it in the plane, we may define the double cover of the plane ramified over the union of these 6 lines. This double cover may be mapped to
is a simple node, the tangent cone to this point is mapped to a conic under the double cover. This conic is in fact tangent to the six lines (w.o proof). Conversely, given a configuration of a conic and six lines which tangent to it in the plane, we may define the double cover of the plane ramified over the union of these 6 lines. This double cover may be mapped to  , under a map which blows down the double cover of the special conic, and is an isomorphism elsewhere (w.o. proof).
, under a map which blows down the double cover of the special conic, and is an isomorphism elsewhere (w.o. proof).The double plane and Kummer varieties of Jacobians
Starting from a smooth curve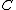 of genus 2, we may identify the Jacobian
of genus 2, we may identify the Jacobian 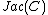
with
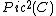 under the map
under the map 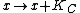 . We now observe two facts: Since
. We now observe two facts: Since 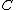 is a hyperelliptic curve the map from the symmetric product
is a hyperelliptic curve the map from the symmetric product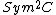 to
to  , defined by
, defined by  , is the blow down of the diagonal to the canonical divisor class. Moreover, the canonical map
, is the blow down of the diagonal to the canonical divisor class. Moreover, the canonical map  is a double cover. Hence we get a double cover
is a double cover. Hence we get a double cover  .
.This double cover is the one which already appeared above: The 6 lines are the images of the odd symmetric theta divisors on
 , while the conic is the image of the blown-up 0. The conic is isomorphic to the canonical system via the isomorphism
, while the conic is the image of the blown-up 0. The conic is isomorphic to the canonical system via the isomorphism  , and each of the six lines is naturally isomorphic to the dual canonical system
, and each of the six lines is naturally isomorphic to the dual canonical system 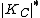 via the identification of theta divisors and translates of the curve
via the identification of theta divisors and translates of the curve  . There is a 1-1 correspondence between pairs of odd symmetric theta divisors and 2-torsion points on the Jacobian given by the fact that
. There is a 1-1 correspondence between pairs of odd symmetric theta divisors and 2-torsion points on the Jacobian given by the fact that 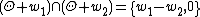 , where
, where  are Weierstrass points (which are the odd theta characteristics in this in genus 2). Hence the branch points of the canonical map
are Weierstrass points (which are the odd theta characteristics in this in genus 2). Hence the branch points of the canonical map 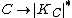 appear on each of these copies of the canonical system as the intersection points of the lines and the tangency points of the lines and the conic.
appear on each of these copies of the canonical system as the intersection points of the lines and the tangency points of the lines and the conic.Finally, since we know that every Kummer quartic is a Kummer variety of a Jacobian of a hyperelliptic curve, we show how to reconstruct Kummer quartic surface directly from the Jacobian of a genus 2 curve: The Jacobian of
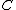 maps to the complete linear system
maps to the complete linear systemLinear system
A linear system is a mathematical model of a system based on the use of a linear operator.Linear systems typically exhibit features and properties that are much simpler than the general, nonlinear case....
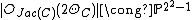 (see the article on Abelian varieties
(see the article on Abelian varietiesAbelian variety
In mathematics, particularly in algebraic geometry, complex analysis and number theory, an abelian variety is a projective algebraic variety that is also an algebraic group, i.e., has a group law that can be defined by regular functions...
). This maps factors through the Kummer variety as a degree 4 map which has 16 nodes at the images of the 2-torsion points on
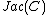 .
. Kummer's 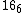 configuration
configuration
There are several crucial points which relate the geometric, algebraic, and combinatorial aspects of the configuration of the nodes of the kummer quartic:- Any symmetric odd theta divisor on
 is given by the set points
is given by the set points  , where w is a Weierstrass point on
, where w is a Weierstrass point on 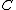 . This theta divisor contains six 2-torsion points:
. This theta divisor contains six 2-torsion points: 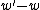 such that
such that  is a Weierstrass point.
is a Weierstrass point. - Two odd theta divisors given by Weierstrass points
 intersect at
intersect at 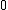 and at
and at 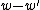 .
. - The translation of the Jacobian by a two torsion point is an isomorphism of the Jacobian as an algebraic surface, which maps the set of 2-torsion points to itself.
- In the complete linear system
 on
on 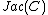 , any odd theta divisor is mapped to a conic, which is the intersection of the Kummer quartic with a plane. Moreover, this complete linear system is invariant under shifts by 2-torsion points.
, any odd theta divisor is mapped to a conic, which is the intersection of the Kummer quartic with a plane. Moreover, this complete linear system is invariant under shifts by 2-torsion points.
Hence we have a configuration of
 conics in
conics in 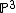 ; where each contains 6 nodes, and such that the intersection of each two is along 2 nodes. This configuration is called the
; where each contains 6 nodes, and such that the intersection of each two is along 2 nodes. This configuration is called the 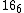 configuration.
configuration.The Weil Pairing
The 2-torsion points on an Abelian variety admit a symplectic bilinear form called the Weil pairing. In the case of Jacobians of curves of genus two, every non trivial 2-torsion point is uniquely expressed as a difference between two of the six Weierstrass points of the curve. The Weil pairing is given in this case by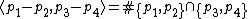 . One can recover a lot of the group theoretic invariants of the group
. One can recover a lot of the group theoretic invariants of the group 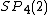 via the geometry of the
via the geometry of the  configuration.
configuration.Group theory, algebra and geometry
Below we give a list of group theoretic invariants and their geometric incarnation in the 166 configuration.- Polar lines
- Apolar complexes
- Klein's 6015 configuration
- Fundamental quadrics
- Fundamental tetrahedra
- Rosenheim tetrads
- Gopel tetrads

