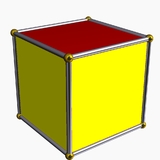
Zonohedron
Encyclopedia
A zonohedron is a convex polyhedron
where every face is a polygon
with point symmetry
or, equivalently, symmetry under rotation
s through 180°. Any zonohedron may equivalently be described as the Minkowski sum
of a set of line segments in three-dimensional space, or as the three-dimensional projection
of a hypercube
. Zonohedra were originally defined and studied by E. S. Fedorov, a Russian crystallographer
. More generally, in any dimension, the Minkowski sum of line segments forms a polytope
known as a zonotope.
of any lattice
forms a convex uniform honeycomb
in which the cells are zonohedra. Any zonohedron formed in this way can tessellate
3-dimensional space and is called a primary parallelohedron. Each primary parallelohedron is combinatorially equivalent to one of five types: the rhombohedron
(including the cube
), hexagonal prism
, truncated octahedron
, rhombic dodecahedron
, and the rhombo-hexagonal dodecahedron
.
{xivi|0≤xi≤1}. The Minkowski sum
{Σxivi|0≤xi≤1} forms a zonohedron, and all zonohedra that contain the origin have this form. The vectors from which the zonohedron is formed are called its generators. This characterization allows the definition of zonohedra to be generalized to higher dimensions, giving zonotopes.
Each edge in a zonohedron is parallel to at least one of the generators, and has length equal to the sum of the lengths of the generators to which it is parallel. Therefore, by choosing a set of generators with no parallel pairs of vectors, and by setting all vector lengths equal, we may form an equilateral
version of any combinatorial type of zonohedron.
By choosing sets of vectors with high degrees of symmetry, we can form in this way, zonohedra with at least as much symmetry. For instance, generators equally spaced around the equator of a sphere, together with another pair of generators through the poles of the sphere, form zonohedra in the form of prism
over regular 2k-gons: the cube
, hexagonal prism
, octagonal prism
, decagonal prism
, dodecagonal prism
, etc.
Generators parallel to the edges of an octahedron form a truncated octahedron
, and generators parallel to the long diagonals of a cube form a rhombic dodecahedron
.
The Minkowski sum of any two zonohedra is another zonohedron, generated by the union of the generators of the two given zonohedra. Thus, the Minkowski sum of a cube and a Truncated octahedron forms the great rhombicuboctahedron, while the Minkowski sum of the cube and the rhombic dodecahedron forms the truncated rhombic dodecahedron
. Both of these zonohedra are simple (three faces meet at each vertex), as is the truncated small rhombicuboctahedron formed from the Minkowski sum of the cube, truncated octahedron, and rhombic dodecahedron.
of any convex polyhedron maps each face of the polygon to a point on the unit sphere, and maps each edge of the polygon separating a pair of faces to a great circle
arc connecting the corresponding two points. In the case of a zonohedron, the edges surrounding each face can be grouped into pairs of parallel edges, and when translated via the Gauss map any such pair becomes a pair of contiguous segments on the same great circle. Thus, the edges of the zonohedron can be grouped into zones of parallel edges, which correspond to the segments of a common great circle on the Gauss map, and the 1-skeleton of the zonohedron can be viewed as the planar dual graph
to an arrangement of great circles on the sphere. Conversely any arrangement of great circles may be formed from the Gauss map of a zonohedron generated by vectors perpendicular to the planes through the circles.
Any simple zonohedron corresponds in this way to a simplicial arrangement, one in which each face is a triangle. Simplicial arrangements of great circles correspond via central projection to simplicial arrangements of lines
in the projective plane
, which were studied by Grünbaum
(1972). He listed three infinite families of simplicial arrangements, one of which leads to the prisms when converted to zonohedra, and the other two of which correspond to additional infinite families of simple zonohedra. There are also many known examples that do not fit into these three families.
over a regular polygon with an even number of sides forms a zonohedron. These prisms can be formed so that all faces are regular: two opposite faces are equal to the regular polygon from which the prism was formed, and these are connected by a sequence of square faces. Zonohedra of this type are the cube
, hexagonal prism
, octagonal prism
, decagonal prism
, dodecagonal prism
, etc.
In addition to this infinite family of regular-faced zonohedra, there are three Archimedean solid
s, all omnitruncations of the regular forms:
In addition, certain Catalan solid
s (duals of Archimedean solids) are again zonohedra:
Others with all rhombic faces:
), it is known that any two zonohedra of equal volumes can be dissected into each other.
called a zonotope. The facets of any zonotope are themselves zonotopes of one lower dimension. Examples of four-dimensional zonotopes include the tesseract
(Minkowski sums of d mutually perpendicular equal length line segments), the omnitruncated 5-cell, and the truncated 24-cell
. Every permutohedron
is a zonotope.
Polyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
where every face is a polygon
Polygon
In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
with point symmetry
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
or, equivalently, symmetry under rotation
Rotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
s through 180°. Any zonohedron may equivalently be described as the Minkowski sum
Minkowski addition
In geometry, the Minkowski sum of two sets A and B in Euclidean space is the result of adding every element of A to every element of B, i.e...
of a set of line segments in three-dimensional space, or as the three-dimensional projection
Projection (mathematics)
Generally speaking, in mathematics, a projection is a mapping of a set which is idempotent, which means that a projection is equal to its composition with itself. A projection may also refer to a mapping which has a left inverse. Bot notions are strongly related, as follows...
of a hypercube
Hypercube
In geometry, a hypercube is an n-dimensional analogue of a square and a cube . It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.An...
. Zonohedra were originally defined and studied by E. S. Fedorov, a Russian crystallographer
Crystallography
Crystallography is the experimental science of the arrangement of atoms in solids. The word "crystallography" derives from the Greek words crystallon = cold drop / frozen drop, with its meaning extending to all solids with some degree of transparency, and grapho = write.Before the development of...
. More generally, in any dimension, the Minkowski sum of line segments forms a polytope
Polytope
In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...
known as a zonotope.
Zonohedra that tile space
The original motivation for studying zonohedra is that the Voronoi diagramVoronoi diagram
In mathematics, a Voronoi diagram is a special kind of decomposition of a given space, e.g., a metric space, determined by distances to a specified family of objects in the space...
of any lattice
Lattice (group)
In mathematics, especially in geometry and group theory, a lattice in Rn is a discrete subgroup of Rn which spans the real vector space Rn. Every lattice in Rn can be generated from a basis for the vector space by forming all linear combinations with integer coefficients...
forms a convex uniform honeycomb
Convex uniform honeycomb
In geometry, a convex uniform honeycomb is a uniform tessellation which fills three-dimensional Euclidean space with non-overlapping convex uniform polyhedral cells.Twenty-eight such honeycombs exist:* the familiar cubic honeycomb and 7 truncations thereof;...
in which the cells are zonohedra. Any zonohedron formed in this way can tessellate
Honeycomb (geometry)
In geometry, a honeycomb is a space filling or close packing of polyhedral or higher-dimensional cells, so that there are no gaps. It is an example of the more general mathematical tiling or tessellation in any number of dimensions....
3-dimensional space and is called a primary parallelohedron. Each primary parallelohedron is combinatorially equivalent to one of five types: the rhombohedron
Rhombohedron
In geometry, a rhombohedron is a three-dimensional figure like a cube, except that its faces are not squares but rhombi. It is a special case of a parallelepiped where all edges are the same length....
(including the cube
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
), hexagonal prism
Hexagonal prism
In geometry, the hexagonal prism is a prism with hexagonal base. The shape has 8 faces, 18 edges, and 12 vertices.Since it has eight faces, it is an octahedron. However, the term octahedron is primarily used to refer to the regular octahedron, which has eight triangular faces...
, truncated octahedron
Truncated octahedron
In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron....
, rhombic dodecahedron
Rhombic dodecahedron
In geometry, the rhombic dodecahedron is a convex polyhedron with 12 rhombic faces. It is an Archimedean dual solid, or a Catalan solid. Its dual is the cuboctahedron.-Properties:...
, and the rhombo-hexagonal dodecahedron
Rhombo-hexagonal dodecahedron
The rhombo-hexagonal dodecahedron is a convex polyhedron with 8 rhombic and 4 equilateral hexagonal faces.It is also called an elongated dodecahedron and extended rhombic dodecahedron because it is related to the rhombic dodecahedron by expanding four rhombic faces of the rhombic dodecahedron into...
.
Zonohedra from Minkowski sums
Let {v0, v1, ...} be a collection of three-dimensional vectors. With each vector vi we may associate a line segmentLine segment
In geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...
{xivi|0≤xi≤1}. The Minkowski sum
Minkowski addition
In geometry, the Minkowski sum of two sets A and B in Euclidean space is the result of adding every element of A to every element of B, i.e...
{Σxivi|0≤xi≤1} forms a zonohedron, and all zonohedra that contain the origin have this form. The vectors from which the zonohedron is formed are called its generators. This characterization allows the definition of zonohedra to be generalized to higher dimensions, giving zonotopes.
Each edge in a zonohedron is parallel to at least one of the generators, and has length equal to the sum of the lengths of the generators to which it is parallel. Therefore, by choosing a set of generators with no parallel pairs of vectors, and by setting all vector lengths equal, we may form an equilateral
Equilateral
In geometry, an equilateral polygon is a polygon which has all sides of the same length.For instance, an equilateral triangle is a triangle of equal edge lengths...
version of any combinatorial type of zonohedron.
By choosing sets of vectors with high degrees of symmetry, we can form in this way, zonohedra with at least as much symmetry. For instance, generators equally spaced around the equator of a sphere, together with another pair of generators through the poles of the sphere, form zonohedra in the form of prism
Prism (geometry)
In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a...
over regular 2k-gons: the cube
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
, hexagonal prism
Hexagonal prism
In geometry, the hexagonal prism is a prism with hexagonal base. The shape has 8 faces, 18 edges, and 12 vertices.Since it has eight faces, it is an octahedron. However, the term octahedron is primarily used to refer to the regular octahedron, which has eight triangular faces...
, octagonal prism
Octagonal prism
In geometry, the octagonal prism is the sixth in an infinite set of prisms, formed by square sides and two regular octagon caps.If faces are all regular, it is a semiregular polyhedron.- Use :...
, decagonal prism
Decagonal prism
In geometry, the decagonal prism is the eighth in an infinite set of prisms, formed by ten square side faces and two regular decagon caps. With twelve faces, it is one of many nonregular dodecahedra.If faces are all regular, it is a semiregular polyhedron....
, dodecagonal prism
Dodecagonal prism
In geometry, the dodecagonal prism is the tenth in an infinite set of prisms, formed by square sides and two regular dodecagon caps.If faces are all regular, it is a semiregular polyhedron.- Use :...
, etc.
Generators parallel to the edges of an octahedron form a truncated octahedron
Truncated octahedron
In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron....
, and generators parallel to the long diagonals of a cube form a rhombic dodecahedron
Rhombic dodecahedron
In geometry, the rhombic dodecahedron is a convex polyhedron with 12 rhombic faces. It is an Archimedean dual solid, or a Catalan solid. Its dual is the cuboctahedron.-Properties:...
.
The Minkowski sum of any two zonohedra is another zonohedron, generated by the union of the generators of the two given zonohedra. Thus, the Minkowski sum of a cube and a Truncated octahedron forms the great rhombicuboctahedron, while the Minkowski sum of the cube and the rhombic dodecahedron forms the truncated rhombic dodecahedron
Truncated rhombic dodecahedron
The truncated rhombic dodecahedron is a convex polyhedron constructed from the rhombic dodecahedron by truncating the 6 vertices.The 6 vertices are truncated such that all edges are equal length. The original 12 rhombic faces become flattened hexagons, and the truncated vertices become squares.The...
. Both of these zonohedra are simple (three faces meet at each vertex), as is the truncated small rhombicuboctahedron formed from the Minkowski sum of the cube, truncated octahedron, and rhombic dodecahedron.
Zonohedra from arrangements
The Gauss mapGauss map
In differential geometry, the Gauss map maps a surface in Euclidean space R3 to the unit sphere S2. Namely, given a surface X lying in R3, the Gauss map is a continuous map N: X → S2 such that N is a unit vector orthogonal to X at p, namely the normal vector to X at p.The Gauss map can be defined...
of any convex polyhedron maps each face of the polygon to a point on the unit sphere, and maps each edge of the polygon separating a pair of faces to a great circle
Great circle
A great circle, also known as a Riemannian circle, of a sphere is the intersection of the sphere and a plane which passes through the center point of the sphere, as opposed to a general circle of a sphere where the plane is not required to pass through the center...
arc connecting the corresponding two points. In the case of a zonohedron, the edges surrounding each face can be grouped into pairs of parallel edges, and when translated via the Gauss map any such pair becomes a pair of contiguous segments on the same great circle. Thus, the edges of the zonohedron can be grouped into zones of parallel edges, which correspond to the segments of a common great circle on the Gauss map, and the 1-skeleton of the zonohedron can be viewed as the planar dual graph
Planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
to an arrangement of great circles on the sphere. Conversely any arrangement of great circles may be formed from the Gauss map of a zonohedron generated by vectors perpendicular to the planes through the circles.
Any simple zonohedron corresponds in this way to a simplicial arrangement, one in which each face is a triangle. Simplicial arrangements of great circles correspond via central projection to simplicial arrangements of lines
Arrangement of lines
In geometry an arrangement of lines is the partition of the plane formed by a collection of lines. Bounds on the complexity of arrangements have been studied in discrete geometry, and computational geometers have found algorithms for the efficient construction of arrangements.-Definition:For any...
in the projective plane
Projective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...
, which were studied by Grünbaum
Branko Grünbaum
Branko Grünbaum is a Croatian-born mathematician and a professor emeritus at the University of Washington in Seattle. He received his Ph.D. in 1957 from Hebrew University of Jerusalem in Israel....
(1972). He listed three infinite families of simplicial arrangements, one of which leads to the prisms when converted to zonohedra, and the other two of which correspond to additional infinite families of simple zonohedra. There are also many known examples that do not fit into these three families.
Types of Zonohedra
We have already seen that any prismPrism (geometry)
In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a...
over a regular polygon with an even number of sides forms a zonohedron. These prisms can be formed so that all faces are regular: two opposite faces are equal to the regular polygon from which the prism was formed, and these are connected by a sequence of square faces. Zonohedra of this type are the cube
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
, hexagonal prism
Hexagonal prism
In geometry, the hexagonal prism is a prism with hexagonal base. The shape has 8 faces, 18 edges, and 12 vertices.Since it has eight faces, it is an octahedron. However, the term octahedron is primarily used to refer to the regular octahedron, which has eight triangular faces...
, octagonal prism
Octagonal prism
In geometry, the octagonal prism is the sixth in an infinite set of prisms, formed by square sides and two regular octagon caps.If faces are all regular, it is a semiregular polyhedron.- Use :...
, decagonal prism
Decagonal prism
In geometry, the decagonal prism is the eighth in an infinite set of prisms, formed by ten square side faces and two regular decagon caps. With twelve faces, it is one of many nonregular dodecahedra.If faces are all regular, it is a semiregular polyhedron....
, dodecagonal prism
Dodecagonal prism
In geometry, the dodecagonal prism is the tenth in an infinite set of prisms, formed by square sides and two regular dodecagon caps.If faces are all regular, it is a semiregular polyhedron.- Use :...
, etc.
In addition to this infinite family of regular-faced zonohedra, there are three Archimedean solid
Archimedean solid
In geometry an Archimedean solid is a highly symmetric, semi-regular convex polyhedron composed of two or more types of regular polygons meeting in identical vertices...
s, all omnitruncations of the regular forms:
- The truncated octahedronTruncated octahedronIn geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron....
, with 6 square and 8 hexagonal faces. (Omnitruncated tetrahedron) - The great rhombicuboctahedron, with 12 squares, 8 hexagons, and 6 octagons. (Omnitruncated cube)
- The great rhombicosidodecahedron, with 30 squares, 20 hexagons and 12 decagons. (Omnitruncated dodecahedron)
In addition, certain Catalan solid
Catalan solid
In mathematics, a Catalan solid, or Archimedean dual, is a dual polyhedron to an Archimedean solid. The Catalan solids are named for the Belgian mathematician, Eugène Catalan, who first described them in 1865....
s (duals of Archimedean solids) are again zonohedra:
- The rhombic dodecahedronRhombic dodecahedronIn geometry, the rhombic dodecahedron is a convex polyhedron with 12 rhombic faces. It is an Archimedean dual solid, or a Catalan solid. Its dual is the cuboctahedron.-Properties:...
is the dual of the cuboctahedronCuboctahedronIn geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,...
. - The rhombic triacontahedronRhombic triacontahedronIn geometry, the rhombic triacontahedron is a convex polyhedron with 30 rhombic faces. It is an Archimedean dual solid, or a Catalan solid. It is the polyhedral dual of the icosidodecahedron, and it is a zonohedron....
is the dual of the icosidodecahedronIcosidodecahedronIn geometry, an icosidodecahedron is a polyhedron with twenty triangular faces and twelve pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon...
.
Others with all rhombic faces:
- Rhombic icosahedronRhombic icosahedronA rhombic icosahedron is a polyhedron shaped like an oblate sphere.It is composed of 20 rhombic faces, of which three, four, or five meet at each vertex...
- RhombohedronRhombohedronIn geometry, a rhombohedron is a three-dimensional figure like a cube, except that its faces are not squares but rhombi. It is a special case of a parallelepiped where all edges are the same length....
- Rhombic enneacontahedronRhombic enneacontahedronA rhombic enneacontahedron is a polyhedron composed of 90 rhombic faces; with three, five, or six rhombi meeting at each vertex. It has 60 broad rhombi and 30 slim...
| zonohedron | image | number of generators |
regular face Regular polygon A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:... |
face-transitive | edge-transitive | vertex-transitive Vertex-transitive In geometry, a polytope is isogonal or vertex-transitive if, loosely speaking, all its vertices are the same... |
cell-transitive space-filling Honeycomb (geometry) In geometry, a honeycomb is a space filling or close packing of polyhedral or higher-dimensional cells, so that there are no gaps. It is an example of the more general mathematical tiling or tessellation in any number of dimensions.... |
simple Simple polytope In geometry, a d-dimensional simple polytope is a d-dimensional polytope each of whose vertices are adjacent to exactly d edges . The vertex figure of a simple d-polytope is a -simplex.... |
|---|---|---|---|---|---|---|---|---|
| cube Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... 4.4.4 |
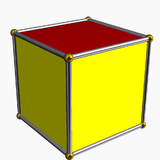 |
3 | ||||||
| hexagonal prism Hexagonal prism In geometry, the hexagonal prism is a prism with hexagonal base. The shape has 8 faces, 18 edges, and 12 vertices.Since it has eight faces, it is an octahedron. However, the term octahedron is primarily used to refer to the regular octahedron, which has eight triangular faces... 4.4.6 |
 |
4 | ||||||
| 2n-prism (n > 3) Prism (geometry) In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a... 4.4.2n |
 |
n + 1 | ||||||
| truncated octahedron Truncated octahedron In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron.... 4.6.6 |
 |
6 | ||||||
| Truncated cuboctahedron Truncated cuboctahedron In geometry, the truncated cuboctahedron is an Archimedean solid. It has 12 square faces, 8 regular hexagonal faces, 6 regular octagonal faces, 48 vertices and 72 edges... 4.6.8 |
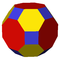 |
8 | ||||||
| Truncated icosidodecahedron Truncated icosidodecahedron In geometry, the truncated icosidodecahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed by two or more types of regular polygon faces.... 4.6.10 |
 |
15 | ||||||
| rhombic dodecahedron Rhombic dodecahedron In geometry, the rhombic dodecahedron is a convex polyhedron with 12 rhombic faces. It is an Archimedean dual solid, or a Catalan solid. Its dual is the cuboctahedron.-Properties:... V3.4.3.4 |
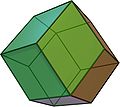 |
4 | ||||||
| rhombic triacontahedron Rhombic triacontahedron In geometry, the rhombic triacontahedron is a convex polyhedron with 30 rhombic faces. It is an Archimedean dual solid, or a Catalan solid. It is the polyhedral dual of the icosidodecahedron, and it is a zonohedron.... V3.5.3.5 |
 |
6 | ||||||
| rhombo-hexagonal dodecahedron Rhombo-hexagonal dodecahedron The rhombo-hexagonal dodecahedron is a convex polyhedron with 8 rhombic and 4 equilateral hexagonal faces.It is also called an elongated dodecahedron and extended rhombic dodecahedron because it is related to the rhombic dodecahedron by expanding four rhombic faces of the rhombic dodecahedron into... |
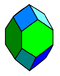 |
5 | ||||||
| truncated rhombic dodecahedron Truncated rhombic dodecahedron The truncated rhombic dodecahedron is a convex polyhedron constructed from the rhombic dodecahedron by truncating the 6 vertices.The 6 vertices are truncated such that all edges are equal length. The original 12 rhombic faces become flattened hexagons, and the truncated vertices become squares.The... |
 |
7 |
Dissection of zonohedra
Although it is not generally true that any polyhedron has a dissection into any other polyhedron of the same volume (see Hilbert's third problemHilbert's third problem
The third on Hilbert's list of mathematical problems, presented in 1900, is the easiest one. The problem is related to the following question: given any two polyhedra of equal volume, is it always possible to cut the first into finitely many polyhedral pieces which can be reassembled to yield the...
), it is known that any two zonohedra of equal volumes can be dissected into each other.
Zonotopes
The Minkowski sum of line segments in any dimension forms a type of polytopePolytope
In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...
called a zonotope. The facets of any zonotope are themselves zonotopes of one lower dimension. Examples of four-dimensional zonotopes include the tesseract
Tesseract
In geometry, the tesseract, also called an 8-cell or regular octachoron or cubic prism, is the four-dimensional analog of the cube. The tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of 6 square faces, the hypersurface of the tesseract consists of 8...
(Minkowski sums of d mutually perpendicular equal length line segments), the omnitruncated 5-cell, and the truncated 24-cell
Truncated 24-cell
In geometry, a truncated 5-cell is a uniform polychoron formed as the truncation of the regular 5-cell.There are two degrees of trunctions, including a bitruncation.- Truncated 5-cell:...
. Every permutohedron
Permutohedron
In mathematics, the permutohedron of order n is an -dimensional polytope embedded in an n-dimensional space, the vertices of which are formed by permuting the coordinates of the vector .-History:According to , permutohedra were first studied by...
is a zonotope.

