
Znám's problem
Encyclopedia
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, Znám's problem asks which sets of k integers have the property that each integer in the set is a proper divisor of the product of the other integers in the set, plus 1. Znám's problem is named after the Slovak mathematician Štefan Znám
Štefan Znám
Štefan Znám was a Slovak mathematician, believed to be the first to ponder Znám's problem in modern times....
, who suggested it in 1972, although other mathematicians had considered similar problems around the same time. One closely related problem drops the assumption of properness of the divisor, and will be called the improper Znám problem hereafter.
One solution to the improper Znám problem is easily provided for any k: the first k terms of Sylvester's sequence
Sylvester's sequence
In number theory, Sylvester's sequence is an integer sequence in which each member of the sequence is the product of the previous members, plus one. The first few terms of the sequence are:...
have the required property. showed that there is at least one solution to the (proper) Znám problem for each k ≥ 5. Sun's solution is based on a recurrence similar to that for Sylvester's sequence, but with a different set of initial values.
The Znám problem is closely related to Egyptian fractions. It is known that there are only finitely many solutions for any fixed k. It is unknown whether there are any solutions to Znám's problem using only odd numbers, and there remain several other open questions.
The problem
Znám's problem asks which sets of integers have the property that each integer in the set is a proper divisor of the product of the other integers in the set, plus 1. That is, given k, what sets of integers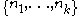
are there, such that, for each i, ni divides but is not equal to

A closely related problem concerns sets of integers in which each integer in the set is a divisor, but not necessarily a proper divisor, of one plus the product of the other integers in the set. This problem does not seem to have been named in the literature, and will be referred to as the improper Znám problem. Any solution to Znám's problem is also a solution to the improper Znám problem, but not necessarily vice versa.
History
Znám's problem is named after the Slovak mathematician Štefan ZnámŠtefan Znám
Štefan Znám was a Slovak mathematician, believed to be the first to ponder Znám's problem in modern times....
, who suggested it in 1972. had posed the improper Znám problem for k = 3, and , independently of Znám, found all solutions to the improper problem for k ≤ 5. showed that Znám's problem is unsolvable for k < 5, and credited J. Janák with finding the solution {2, 3, 11, 23, 31} for k = 5.
Examples
One solution to k = 5 is {2, 3, 7, 47, 395}. A few calculations will show that| 3 × 7 × 47 × 395 | + 1 = | 389866, | which is divisible by but unequal to 2, | |
| 2 × 7 × 47 × 395 | + 1 = | 259911, | which is divisible by but unequal to 3, | |
| 2 × 3 × 47 × 395 | + 1 = | 111391, | which is divisible by but unequal to 7, | |
| 2 × 3 × 7 × 395 | + 1 = | 16591, | which is divisible by but unequal to 47, and | |
| 2 × 3 × 7 × 47 | + 1 = | 1975, | which is divisible by but unequal to 395. |
An interesting "near miss" for k = 4 is the set {2, 3, 7, 43}, formed by taking the first four terms of Sylvester's sequence. It has the property that each integer in the set divides the product of the other integers in the set, plus 1, but the last member of this set is equal to the product of the first three members plus one, rather than being a proper divisor. Thus, it is a solution to the improper Znám problem, but not a solution to Znám's problem as it is usually defined.
Connection to Egyptian fractions
Any solution to the improper Znám problem is equivalent (via division by the product of the xi's) to a solution to the equation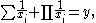
where y as well as each xi must be an integer, and conversely any such solution corresponds to a solution to the improper Znám problem. However, all known solutions have y = 1, so they satisfy the equation
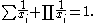
That is, they lead to an Egyptian fraction representation of the number one as a sum of unit fractions. Several of the cited papers on Znám's problem study also the solutions to this equation. describe an application of the equation in topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, to the classification of singularities
Mathematical singularity
In mathematics, a singularity is in general a point at which a given mathematical object is not defined, or a point of an exceptional set where it fails to be well-behaved in some particular way, such as differentiability...
on surfaces, and describe an application to the theory of nondeterministic finite automata.
Number of solutions
As showed, the number of solutions for any k is finite, so it makes sense to count the total number of solutions for each k.Brenton and Vasiliu calculated that the number of solutions for small values of k, starting with k = 5, forms the sequence
- 2, 5, 1818 (number)18 is the natural number following 17 and preceding 19.In speech, the numbers 18 and 80 are sometimes confused. When carefully enunciated, they differ in which syllable is stressed: 18 vs 80 . However, in dates such as 1864, or when contrasting numbers in the teens, such as 17, 18, 19, the stress...
, 9696 (number)96 is the natural number following 95 and preceding 97.-In mathematics:Ninety-six is an octagonal number, a refactorable number and an untouchable number. Since it is a multiple of 6, it is a semiperfect number...
.
Presently, a few solutions are known for k = 9 and k = 10, but it is unclear how many solutions remain undiscovered for those values of k.
However, there are infinitely many solutions if k is not fixed:
showed that there are at least 39 solutions for each k ≥ 12, improving earlier results proving the existence of fewer solutions . conjecture that the number of solutions for each value of k grows monotonically with k.
It is unknown whether there are any solutions to Znám's problem using only odd numbers. With one exception, all known solutions start with 2. If all numbers in a solution to Znám's problem or the improper Znám problem are prime
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
, their product is a primary pseudoperfect number ; it is unknown whether infinitely many solutions of this type exist.

