
Word metric
Encyclopedia
In group theory
, a word metric on a group
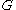 is a way to measure distance between any two elements of
is a way to measure distance between any two elements of 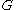 . As the name suggests, the word metric is a metric
. As the name suggests, the word metric is a metric
on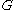 , assigning to any two elements
, assigning to any two elements 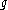 ,
, 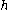 of
of 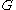 a distance
a distance 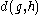 that measures how efficiently their difference
that measures how efficiently their difference 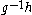 can be expressed as a word whose letters come from a generating set
can be expressed as a word whose letters come from a generating set
for the group. The word metric on G is very closely related to the Cayley graph
of G: the word metric measures the length of the shortest path in the Cayley graph between two elements of G.
A generating set
for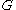 must first be chosen before a word metric on
must first be chosen before a word metric on  is specified. Different choices of a generating set will typically yield different word metrics. While this seems at first to be a weakness in the concept of the word metric, it can be exploited to prove theorems about geometric properties of groups, as is done in geometric group theory
is specified. Different choices of a generating set will typically yield different word metrics. While this seems at first to be a weakness in the concept of the word metric, it can be exploited to prove theorems about geometric properties of groups, as is done in geometric group theory
.
The group
For a more illustrative example, the elements of the group 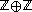 can be thought of as vectors in the Cartesian plane
can be thought of as vectors in the Cartesian plane
with integer coefficients. The group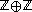 is generated by the standard unit vectors
is generated by the standard unit vectors  ,
, 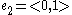 and their inverses
and their inverses  ,
, 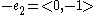 . The Cayley graph
. The Cayley graph
of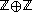 is the so-called taxicab geometry
is the so-called taxicab geometry
. It can be pictured in the plane as an infinite square grid of city streets, where each horizontal and vertical line with integer coordinates is a street, and each point of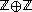 lies at the intersection of a horizontal and a vertical street. Each horizontal segment between two vertices represents the generating vector
lies at the intersection of a horizontal and a vertical street. Each horizontal segment between two vertices represents the generating vector  or
or 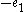 , depending on whether the segment is travelled in the forward or backward direction, and each vertical segment represents
, depending on whether the segment is travelled in the forward or backward direction, and each vertical segment represents 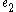 or
or 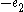 . A car starting from
. A car starting from 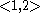 and travelling along the streets to
and travelling along the streets to 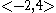 can make the trip by many different routes. But no matter what route is taken, the car must travel at least |1 - (-2)| = 3 horizontal blocks and at least |2 - 4| = 2 vertical blocks, for a total trip distance of at least 3 + 2 = 5. If the car goes out of its way the trip may be longer, but the minimal distance travelled by the car, equal in value to the word metric between <1,2> and <-2,4> is therefore equal to 5.
can make the trip by many different routes. But no matter what route is taken, the car must travel at least |1 - (-2)| = 3 horizontal blocks and at least |2 - 4| = 2 vertical blocks, for a total trip distance of at least 3 + 2 = 5. If the car goes out of its way the trip may be longer, but the minimal distance travelled by the car, equal in value to the word metric between <1,2> and <-2,4> is therefore equal to 5.
In general, given two elements and
and 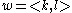 of
of 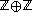 , the distance between
, the distance between  and
and 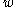 in the word metric is equal to
in the word metric is equal to  .
.
for G, and suppose that S is closed under the inverse operation on G. A word over the set S is just a finite sequence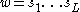 whose entries
whose entries 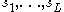 are elements of S. The integer L is called the length of the word
are elements of S. The integer L is called the length of the word 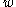 . Using the group operation in G, the entries of a word
. Using the group operation in G, the entries of a word 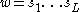 can be multiplied in order, remembering that the entries are elements of G. The result of this multiplication is an element
can be multiplied in order, remembering that the entries are elements of G. The result of this multiplication is an element 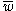 in the group G which is called the evaluation of the word w. As a special case, the empty word
in the group G which is called the evaluation of the word w. As a special case, the empty word 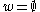 has length zero, and its evaluation is the identity element of G.
has length zero, and its evaluation is the identity element of G.
Given an element g of G, its word norm |g| with respect to the generating set S is defined to be the shortest length of a word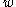 over S whose evaluation
over S whose evaluation 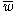 is equal to g. Given two elements g,h in G, the distance d(g,h) in the word metric with respect to S is defined to be
is equal to g. Given two elements g,h in G, the distance d(g,h) in the word metric with respect to S is defined to be 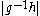 . Equivalently, d(g,h) is the shortest length of a word w over S such that
. Equivalently, d(g,h) is the shortest length of a word w over S such that 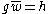 .
.
The word metric on G satisfies the axioms for a metric
, and it is not hard to prove this. The proof of the symmetry axiom d(g,h) = d(h,g) for a metric uses the assumption that the generating set S is closed under inverse.
of G with respect to the generating set S. When each edge of the Cayley graph is assigned a metric of length 1, the distance between two group elements g,h in G is equal to the shortest length of a path in the Cayley graph from the vertex g to the vertex h.
The word metric on G can also be defined without assuming that the generating set S is closed under inverse. To do this, first symmetrize S, replacing it by a larger generating set consisting of each in S as well as its inverse
in S as well as its inverse 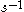 . Then define the word metric with respect to S to be the word metric with respect to the symmetrization of S.
. Then define the word metric with respect to S to be the word metric with respect to the symmetrization of S.
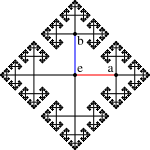 Suppose that F is the free group on the two element set
Suppose that F is the free group on the two element set  . A word w in the symmetric generating set
. A word w in the symmetric generating set 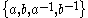 is said to be reduced if the letters
is said to be reduced if the letters 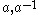 do not occur next to each other in w, nor do the letters
do not occur next to each other in w, nor do the letters 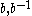 . Every element
. Every element  is represented by a unique reduced word, and this reduced word is the shortest word representing g. For example, since the word
is represented by a unique reduced word, and this reduced word is the shortest word representing g. For example, since the word 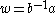 is reduced and has length 2, the word norm of
is reduced and has length 2, the word norm of 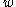 equals 2, so the distance in the word norm between b and
equals 2, so the distance in the word norm between b and 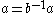 equals 2. This can be visualized in terms of the Cayley graph, where the shortest path between b and a has length 2.
equals 2. This can be visualized in terms of the Cayley graph, where the shortest path between b and a has length 2.
on itself by left multiplication: the action of each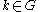 takes each
takes each 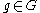 to kg. This action is an isometry
to kg. This action is an isometry
of the word metric. The proof is simple: the distance between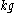 and
and 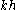 equals
equals 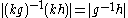 which equals the distance between
which equals the distance between  and
and 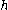 .
.
 ,
, 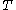 are two symmetric, finite generating sets for G with corresponding word metrics
are two symmetric, finite generating sets for G with corresponding word metrics 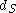 ,
, 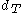 , then there is a constant
, then there is a constant 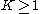 such that for any
such that for any 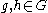 ,
,
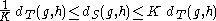 .
.
This constant K is just the maximum of the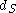 word norms of elements of
word norms of elements of 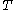 and the
and the 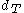 word norms of elements of
word norms of elements of 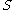 . This proof is also easy: any word over S can be converted by substitution into a word over T, expanding the length of the word by a factor of at most K, and similarly for converting words over T into words over S.
. This proof is also easy: any word over S can be converted by substitution into a word over T, expanding the length of the word by a factor of at most K, and similarly for converting words over T into words over S.
The bilipschitz equivalence of word metrics implies in turn that the growth rate
of a finitely generated group is a well-defined isomorphism invariant of the group, independent of the choice of a finite generating set. This implies in turn that various properties of growth, such as polynomial growth, the degree of polynomial growth, and exponential growth, are isomorphism invariants of groups. This topic is discussed further in the article on the growth rate
of a group.
, groups are studied by their actions
on metric spaces. A principle which generalizes the bilipschitz invariance of word metrics says that any finitely generated word metric on G is quasi-isometric
to any proper, geodesic metric space on which G acts
, properly discontinuously and cocompactly. Metric spaces on which G acts in this manner are called model spaces for G.
It follows in turn that any quasi-isometrically invariant property satisfied by the word metric of G or by any model space of G is an isomorphism invariant of G. Modern geometric group theory
is in large part the study of quasi-isometry invariants.
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, a word metric on a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
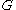 is a way to measure distance between any two elements of
is a way to measure distance between any two elements of 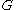 . As the name suggests, the word metric is a metric
. As the name suggests, the word metric is a metricMetric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
on
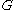 , assigning to any two elements
, assigning to any two elements 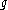 ,
, 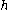 of
of 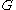 a distance
a distance 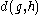 that measures how efficiently their difference
that measures how efficiently their difference 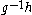 can be expressed as a word whose letters come from a generating set
can be expressed as a word whose letters come from a generating setGenerating set of a group
In abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...
for the group. The word metric on G is very closely related to the Cayley graph
Cayley graph
In mathematics, a Cayley graph, also known as a Cayley colour graph, Cayley diagram, group diagram, or colour group is a graph that encodes the abstract structure of a group. Its definition is suggested by Cayley's theorem and uses a specified, usually finite, set of generators for the group...
of G: the word metric measures the length of the shortest path in the Cayley graph between two elements of G.
A generating set
Generating set
In mathematics, the expressions generator, generate, generated by and generating set can have several closely related technical meanings:...
for
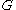 must first be chosen before a word metric on
must first be chosen before a word metric on  is specified. Different choices of a generating set will typically yield different word metrics. While this seems at first to be a weakness in the concept of the word metric, it can be exploited to prove theorems about geometric properties of groups, as is done in geometric group theory
is specified. Different choices of a generating set will typically yield different word metrics. While this seems at first to be a weakness in the concept of the word metric, it can be exploited to prove theorems about geometric properties of groups, as is done in geometric group theoryGeometric group theory
Geometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such groups and topological and geometric properties of spaces on which these groups act .Another important...
.
The group of integers Z
The group of integers Z is generated by the set {-1,+1}. The integer -3 can be expressed as -1-1-1+1-1, a word of length 5 in these generators. But the word which expresses -3 most efficiently is -1-1-1, a word of length 3. The distance between 0 and -3 in the word metric is therefore equal to 3. More generally, the distance between two integers m and n in the word metric is equal to |m-n|, because the shortest word representing the difference m-n has length equal to |m-n|. The group 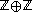
For a more illustrative example, the elements of the group 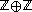 can be thought of as vectors in the Cartesian plane
can be thought of as vectors in the Cartesian planeCartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
with integer coefficients. The group
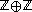 is generated by the standard unit vectors
is generated by the standard unit vectors  ,
, 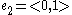 and their inverses
and their inverses  ,
, 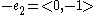 . The Cayley graph
. The Cayley graphCayley graph
In mathematics, a Cayley graph, also known as a Cayley colour graph, Cayley diagram, group diagram, or colour group is a graph that encodes the abstract structure of a group. Its definition is suggested by Cayley's theorem and uses a specified, usually finite, set of generators for the group...
of
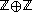 is the so-called taxicab geometry
is the so-called taxicab geometryTaxicab geometry
Taxicab geometry, considered by Hermann Minkowski in the 19th century, is a form of geometry in which the usual distance function or metric of Euclidean geometry is replaced by a new metric in which the distance between two points is the sum of the absolute differences of their coordinates...
. It can be pictured in the plane as an infinite square grid of city streets, where each horizontal and vertical line with integer coordinates is a street, and each point of
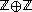 lies at the intersection of a horizontal and a vertical street. Each horizontal segment between two vertices represents the generating vector
lies at the intersection of a horizontal and a vertical street. Each horizontal segment between two vertices represents the generating vector  or
or 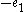 , depending on whether the segment is travelled in the forward or backward direction, and each vertical segment represents
, depending on whether the segment is travelled in the forward or backward direction, and each vertical segment represents 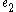 or
or 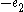 . A car starting from
. A car starting from 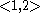 and travelling along the streets to
and travelling along the streets to 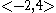 can make the trip by many different routes. But no matter what route is taken, the car must travel at least |1 - (-2)| = 3 horizontal blocks and at least |2 - 4| = 2 vertical blocks, for a total trip distance of at least 3 + 2 = 5. If the car goes out of its way the trip may be longer, but the minimal distance travelled by the car, equal in value to the word metric between <1,2> and <-2,4> is therefore equal to 5.
can make the trip by many different routes. But no matter what route is taken, the car must travel at least |1 - (-2)| = 3 horizontal blocks and at least |2 - 4| = 2 vertical blocks, for a total trip distance of at least 3 + 2 = 5. If the car goes out of its way the trip may be longer, but the minimal distance travelled by the car, equal in value to the word metric between <1,2> and <-2,4> is therefore equal to 5.In general, given two elements
 and
and 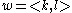 of
of 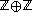 , the distance between
, the distance between  and
and 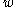 in the word metric is equal to
in the word metric is equal to  .
.Definition
Let G be a group, let S be a generating setGenerating set
In mathematics, the expressions generator, generate, generated by and generating set can have several closely related technical meanings:...
for G, and suppose that S is closed under the inverse operation on G. A word over the set S is just a finite sequence
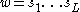 whose entries
whose entries 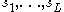 are elements of S. The integer L is called the length of the word
are elements of S. The integer L is called the length of the word 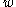 . Using the group operation in G, the entries of a word
. Using the group operation in G, the entries of a word 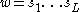 can be multiplied in order, remembering that the entries are elements of G. The result of this multiplication is an element
can be multiplied in order, remembering that the entries are elements of G. The result of this multiplication is an element 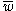 in the group G which is called the evaluation of the word w. As a special case, the empty word
in the group G which is called the evaluation of the word w. As a special case, the empty word 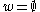 has length zero, and its evaluation is the identity element of G.
has length zero, and its evaluation is the identity element of G.Given an element g of G, its word norm |g| with respect to the generating set S is defined to be the shortest length of a word
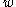 over S whose evaluation
over S whose evaluation 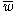 is equal to g. Given two elements g,h in G, the distance d(g,h) in the word metric with respect to S is defined to be
is equal to g. Given two elements g,h in G, the distance d(g,h) in the word metric with respect to S is defined to be 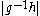 . Equivalently, d(g,h) is the shortest length of a word w over S such that
. Equivalently, d(g,h) is the shortest length of a word w over S such that 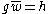 .
.The word metric on G satisfies the axioms for a metric
Metric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
, and it is not hard to prove this. The proof of the symmetry axiom d(g,h) = d(h,g) for a metric uses the assumption that the generating set S is closed under inverse.
Variations
The word metric has an equivalent definition formulated in more geometric terms using the Cayley graphCayley graph
In mathematics, a Cayley graph, also known as a Cayley colour graph, Cayley diagram, group diagram, or colour group is a graph that encodes the abstract structure of a group. Its definition is suggested by Cayley's theorem and uses a specified, usually finite, set of generators for the group...
of G with respect to the generating set S. When each edge of the Cayley graph is assigned a metric of length 1, the distance between two group elements g,h in G is equal to the shortest length of a path in the Cayley graph from the vertex g to the vertex h.
The word metric on G can also be defined without assuming that the generating set S is closed under inverse. To do this, first symmetrize S, replacing it by a larger generating set consisting of each
 in S as well as its inverse
in S as well as its inverse 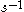 . Then define the word metric with respect to S to be the word metric with respect to the symmetrization of S.
. Then define the word metric with respect to S to be the word metric with respect to the symmetrization of S.Example in a free group

 . A word w in the symmetric generating set
. A word w in the symmetric generating set 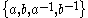 is said to be reduced if the letters
is said to be reduced if the letters 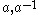 do not occur next to each other in w, nor do the letters
do not occur next to each other in w, nor do the letters 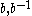 . Every element
. Every element  is represented by a unique reduced word, and this reduced word is the shortest word representing g. For example, since the word
is represented by a unique reduced word, and this reduced word is the shortest word representing g. For example, since the word 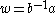 is reduced and has length 2, the word norm of
is reduced and has length 2, the word norm of 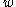 equals 2, so the distance in the word norm between b and
equals 2, so the distance in the word norm between b and 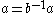 equals 2. This can be visualized in terms of the Cayley graph, where the shortest path between b and a has length 2.
equals 2. This can be visualized in terms of the Cayley graph, where the shortest path between b and a has length 2.Isometry of the left action
The group G actsGroup action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
on itself by left multiplication: the action of each
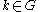 takes each
takes each 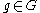 to kg. This action is an isometry
to kg. This action is an isometryIsometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
of the word metric. The proof is simple: the distance between
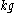 and
and 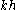 equals
equals 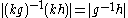 which equals the distance between
which equals the distance between  and
and 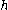 .
.Bilipschitz invariants of a group
The word metric on a group G is not unique, because different symmetric generating sets give different word metrics. However, finitely generated word metrics are unique up to bilipschitz equivalence: if ,
, 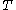 are two symmetric, finite generating sets for G with corresponding word metrics
are two symmetric, finite generating sets for G with corresponding word metrics 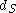 ,
, 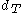 , then there is a constant
, then there is a constant 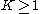 such that for any
such that for any 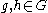 ,
,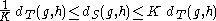 .
.This constant K is just the maximum of the
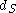 word norms of elements of
word norms of elements of 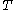 and the
and the 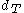 word norms of elements of
word norms of elements of 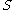 . This proof is also easy: any word over S can be converted by substitution into a word over T, expanding the length of the word by a factor of at most K, and similarly for converting words over T into words over S.
. This proof is also easy: any word over S can be converted by substitution into a word over T, expanding the length of the word by a factor of at most K, and similarly for converting words over T into words over S.The bilipschitz equivalence of word metrics implies in turn that the growth rate
Growth rate (group theory)
In group theory, the growth rate of a group with respect to a symmetric generating set describes the size of balls in the group. Every element in the group can be written as a product of generators, and the growth rate counts the number of elements that can be written as a product of length...
of a finitely generated group is a well-defined isomorphism invariant of the group, independent of the choice of a finite generating set. This implies in turn that various properties of growth, such as polynomial growth, the degree of polynomial growth, and exponential growth, are isomorphism invariants of groups. This topic is discussed further in the article on the growth rate
Growth rate (group theory)
In group theory, the growth rate of a group with respect to a symmetric generating set describes the size of balls in the group. Every element in the group can be written as a product of generators, and the growth rate counts the number of elements that can be written as a product of length...
of a group.
Quasi-isometry invariants of a group
In geometric group theoryGeometric group theory
Geometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such groups and topological and geometric properties of spaces on which these groups act .Another important...
, groups are studied by their actions
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
on metric spaces. A principle which generalizes the bilipschitz invariance of word metrics says that any finitely generated word metric on G is quasi-isometric
Quasi-isometry
In mathematics, a quasi-isometry is a means to compare the large-scale structure of metric spaces. The concept is especially important in Gromov's geometric group theory.-Definition:...
to any proper, geodesic metric space on which G acts
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
, properly discontinuously and cocompactly. Metric spaces on which G acts in this manner are called model spaces for G.
It follows in turn that any quasi-isometrically invariant property satisfied by the word metric of G or by any model space of G is an isomorphism invariant of G. Modern geometric group theory
Geometric group theory
Geometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such groups and topological and geometric properties of spaces on which these groups act .Another important...
is in large part the study of quasi-isometry invariants.

