Wightman axioms
Encyclopedia
In physics
the Wightman axioms are an attempt at a mathematically rigorous formulation of quantum field theory
. Arthur Wightman
formulated the axioms in the early 1950s but they were first published only in 1964, after Haag-Ruelle scattering theory affirmed their significance.
The axioms exist in the context of constructive quantum field theory
, and they are meant to provide a basis for rigorous treatment of quantum fields, and strict foundation for the perturbative methods used. One of the Millennium Problems
is to realize the Wightman axioms in the case of Yang-Mills fields.
upon which the Poincaré group
acts unitarily
. In this way, the concepts of energy, momentum, angular momentum and center of mass (corresponding to boosts) are implemented.
There is also a stability assumption which restricts the spectrum of the four-momentum
to the positive light cone
(and its boundary). However, this isn't enough to implement locality
. For that, the Wightman axioms have position dependent operators called quantum fields which form covariant representations of the Poincaré group.
Since quantum field theory suffers from ultraviolet problems, the value of a field at a point is not well-defined. To get around this, the Wightman axioms introduce the idea of smearing over a test function to tame the UV divergences which arise even in a free field theory. Because the axioms are dealing with unbounded operator
s, the domains of the operators have to be specified.
The Wightman axioms restrict the causal structure of the theory by imposing either commutativity or anticommutativity between spacelike separated fields.
They also postulate the existence of a Poincaré-invariant state called the vacuum
and demand it is unique. Moreover, the axioms assume that the vacuum is "cyclic", i.e., that the set of all vectors which can be obtained by evaluating at the vacuum state elements of the polynomial algebra generated by the smeared field operators is a dense subset of the whole Hilbert space.
Lastly, there is the primitive causality restriction which states that any polynomial in the smeared fields can be arbitrarily accurately approximated (i.e. is the limit of operators in the weak topology
) by polynomials over fields smeared over test functions with support in
any open subspace of Minkowski space
whose causal closure
is the whole Minkowski space itself.
is described according to von Neumann; in particular, the pure states are given by the rays, i.e. the one-dimensional subspaces, of some separable complex Hilbert space
. In the following, the scalar product of Hilbert space vectors Ψ and Φ will be denoted by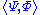
, and the norm of Ψ will be denoted by 
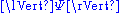. The transition probability between two pure states [Ψ] and [Φ] can be defined in terms of non-zero vector representatives Ψ and Φ to be
and is independent of which representative vectors, Ψ and Φ, are chosen.
The theory of symmetry is described according to Wigner. This is to take advantage of the successful description of relativistic particles by Eugene Paul Wigner in his famous paper of 1939. See Wigner's classification
. Wigner postulated that for the transition probability between states to be the same to all observers related by a transformation of special relativity
. More generally, he considered the statement that a theory be invariant under a group G to be expressed in terms of the invariance of the transition probability between any two rays. The statement postulates that the group acts on the set of rays, that is, on projective space. Let (a,L) be an element of the Poincaré group
(the inhomogeneous Lorentz group). Thus, a is a real Lorentz four-vector
representing the change of space-time origin
where x is in the Minkowski space M4 and L is a Lorentz transformation
, which can be defined as a linear transformation of four-dimensional space-time which preserves the Lorentz distance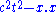
of every vector 
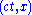. Then the theory is invariant under the Poincaré group if for every ray Ψ of the Hilbert space and every group element (a,L) is given a transformed ray Ψ(a,L)
and the transition probability is unchanged by the transformation:
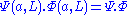
The first theorem of Wigner is that under these conditions, we can express invariance more conveniently in terms of linear or anti-linear operators (indeed, unitary
or antiunitary operators); the symmetry operator on the projective space of rays can be lifted to the underlying Hilbert space.
This being done for each group element (a, L), we get a family of unitary or antiunitary operators U(a, L) on our Hilbert space, such that the ray Ψ transformed by (a, L) is the same as the ray containing U(a, L) ψ. If we
restrict attention to elements of the group connected to the identity, then the anti-unitary case does not occur. Let (a, L) and (b, M) be two Poincaré transformations, and let us denote their group product by (a, L).(b,M); from the physical interpretation we see that the ray containing U(a, L)[U(b, M)]ψ must (for any psi) be the ray containing U((a, L). (b, M))ψ. Therefore these two vectors differ by a phase,
which can depend on the two group elements (a, L) and (b, M). These two vectors do not need to be equal, however. Indeed, for particles of spin 1/2, they cannot be equal for all group elements. By further use of arbitrary phase-changes, Wigner showed that the product of the representing unitary operators
obeys
instead of the group law. For particles of integer spin (pions, photons, gravitons...) one can remove the +/− sign by further phase changes,
but for representations of half-odd-spin, we cannot, and the sign changes discontinuously as we go round any axis by an angle of 2π.
We can, however, construct a representation of the covering group of the Poincare group, called the inhomogeneous SL(2,C); this has elements (a, A)
where as before, a is a four-vector, but now A is a complex 2 × 2 matrix with unit determinant. We denote the unitary operator
s we get by U(a, A), and these give us a continuous, unitary and true representation in that the collection of U(a,A) obey the group law of the inhomogeneous SL(2,C).
Because of the sign-change under rotations by 2π, Hermitian operators transforming as spin 1/2, 3/2 etc., cannot be observable
s. This shows up as the univalence superselection
rule: phases between states of spin 0, 1, 2 etc. and those of spin 1/2, 3/2 etc., are not observable. This rule is in addition to the non-observability of the overall phase of a state vector.
Concerning the observables, and states |v), we get a
representation U(a, L) of Poincaré group
, on integer spin subspaces, and U(a, A) of the inhomogeneous SL(2,C) on half-odd-integer subspaces, which acts according to the following interpretation:
An ensemble corresponding to U(a, L)|v) is to be interpreted with respect to the coordinates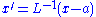
in exactly the same way as an ensemble corresponding to |v) is interpreted with respect to the coordinates x; and similarly for the odd subspaces.
The group of space-time translations is commutative, and so the operators can be simultaneously diagonalised. The generators of these groups give us four self-adjoint operator
s,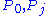
, j = 1, 2, 3, which transform under the homogeneous group as a four-vector, called the energy-momentum four-vector.
The second part of the zeroth axiom of Wightman is that the representation U(a, A) fulfills the spectral condition - that the simultaneous spectrum of energy-momentum is contained in the forward cone:
............... 
which, together with their adjoints, are defined on a dense subset of the Hilbert state space, containing the vacuum. The fields A are operator-valued tempered distribution
s. The Hilbert state space is spanned by the field polynomials acting on the vacuum (cyclicity condition).
, and they transform according to some representation S of the Lorentz group
, or SL(2,C) if the spin is not integer:
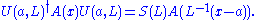
Cyclicity of a vacuum, and uniqueness of a vacuum are sometimes considered separately. Also, there is property of asymptotic completeness - that
Hilbert state space is spanned by the asymptotic spaces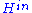
and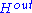 
, appearing in the collision S matrix
. The other
important property of field theory is mass gap
which is not required by
the axioms - that energy-momentum spectrum has a gap between zero and some
positive number.
Arthur Wightman
showed that the vacuum expectation value
distributions, satisfying certain set of properties which follow from the axioms, are sufficient to reconstruct the field theory — Wightman reconstruction theorem, including the existence of a vacuum state
; he did not find the condition on the vacuum expectation values guaranteeing the uniqueness of the vacuum; this condition, the cluster property
, was found later by Res Jost
, Klaus Hepp
, David Ruelle
and Othmar Steinmann.
If the theory has a mass gap
, i.e. there are no masses between 0 and some constant greater than zero, then vacuum expectation
distributions are asymptotically independent in distant regions.
Haag's theorem
says that there can be no interaction picture — that we cannot use the Fock space
of noninteracting particles as a Hilbert space — in the sense that we would identify Hilbert spaces via field polynomials acting on a vacuum at a certain time.
Unlike local quantum field theory
, the Wightman axioms restrict the causal structure of the theory explicitly by imposing either commutativity or anticommutativity between spacelike separated fields, instead of deriving the causal structure as a theorem. If one considers a generalization of the Wightman axioms to dimensions other than 4, this (anti)commutativity postulate rules out anyon
s and braid statistics
in lower dimensions.
The Wightman postulate of a unique vacuum state doesn't necessarily make the Wightman axioms inappropriate for the case of spontaneous symmetry breaking
because we can always restrict ourselves to a superselection sector
.
The cyclicity of the vacuum demanded by the Wightman axioms means that they describe only the superselection sector of the vacuum; again, that is not a great loss of generality. However, this assumption does leave out finite energy states like solitons which can't be generated by a polynomial of fields smeared by test functions because a soliton, at least from a field theoretic perspective, is a global structure involving topological boundary conditions at infinity.
The Wightman framework does not cover effective field theories
because there is no limit as to how small the support of a test function can be. I.e., there is no cutoff
scale.
The Wightman framework also does not cover gauge theories
. Even in Abelian gauge theories conventional approaches start off with a "Hilbert space" (it's not a Hilbert space, but physicists call it a Hilbert space) with an indefinite norm and the physical states and physical operators belong to a cohomology
. This obviously is not covered anywhere in the Wightman framework. (However as shown by Schwinger, Christ and Lee, Gribov, Zwanziger, Van Baal, etc., canonical quantization of gauge theories in Coulomb gauge is possible with an ordinary Hilbert space, and this might be the way to make them fall under the applicability of the axiom systematics.)
The Wightman axioms can be rephrased in terms of a state called a Wightman functional on a Borchers algebra
equal to the tensor algebra of a space of test functions.
Currently, there is no proof that the Wightman axioms can be satisfied for interacting theories in dimension 4. In particular, the Standard model
of particle physics has no mathematically rigorous foundations. There is a million dollar prize for a proof that the Wightman axioms can be satisfied for gauge theories, with the additional requirement of a mass gap.
QFT can be Wick-rotated
into a Wightman QFT. See Osterwalder-Schrader theorem. This theorem is the key tool for the constructions of interacting theories in dimension 2 and 3 which satisfy the Wightman axioms.
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
the Wightman axioms are an attempt at a mathematically rigorous formulation of quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
. Arthur Wightman
Arthur Wightman
Arthur Strong Wightman is an American mathematical physicist. He is one of the founders of the axiomatic approach to quantum field theory, and originated the set of Wightman axioms....
formulated the axioms in the early 1950s but they were first published only in 1964, after Haag-Ruelle scattering theory affirmed their significance.
The axioms exist in the context of constructive quantum field theory
Constructive quantum field theory
In mathematical physics, constructive quantum field theory is the field devoted to showing that quantum theory is mathematically compatible with special relativity. This demonstration requires new mathematics, in a sense analogous to Newton developing calculus in order to understand planetary...
, and they are meant to provide a basis for rigorous treatment of quantum fields, and strict foundation for the perturbative methods used. One of the Millennium Problems
Millennium Prize Problems
The Millennium Prize Problems are seven problems in mathematics that were stated by the Clay Mathematics Institute in 2000. As of September 2011, six of the problems remain unsolved. A correct solution to any of the problems results in a US$1,000,000 prize being awarded by the institute...
is to realize the Wightman axioms in the case of Yang-Mills fields.
Rationale
One basic idea of the Wightman axioms is that there is a Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
upon which the Poincaré group
Poincaré group
In physics and mathematics, the Poincaré group, named after Henri Poincaré, is the group of isometries of Minkowski spacetime.-Simple explanation:...
acts unitarily
Unitary representation
In mathematics, a unitary representation of a group G is a linear representation π of G on a complex Hilbert space V such that π is a unitary operator for every g ∈ G...
. In this way, the concepts of energy, momentum, angular momentum and center of mass (corresponding to boosts) are implemented.
There is also a stability assumption which restricts the spectrum of the four-momentum
Four-momentum
In special relativity, four-momentum is the generalization of the classical three-dimensional momentum to four-dimensional spacetime. Momentum is a vector in three dimensions; similarly four-momentum is a four-vector in spacetime...
to the positive light cone
Light cone
A light cone is the path that a flash of light, emanating from a single event and traveling in all directions, would take through spacetime...
(and its boundary). However, this isn't enough to implement locality
Principle of locality
In physics, the principle of locality states that an object is influenced directly only by its immediate surroundings. Experiments have shown that quantum mechanically entangled particles must violate either the principle of locality or the form of philosophical realism known as counterfactual...
. For that, the Wightman axioms have position dependent operators called quantum fields which form covariant representations of the Poincaré group.
Since quantum field theory suffers from ultraviolet problems, the value of a field at a point is not well-defined. To get around this, the Wightman axioms introduce the idea of smearing over a test function to tame the UV divergences which arise even in a free field theory. Because the axioms are dealing with unbounded operator
Unbounded operator
In mathematics, more specifically functional analysis and operator theory, the notion of unbounded operator provides an abstract framework for dealing with differential operators, unbounded observables in quantum mechanics, and other cases....
s, the domains of the operators have to be specified.
The Wightman axioms restrict the causal structure of the theory by imposing either commutativity or anticommutativity between spacelike separated fields.
They also postulate the existence of a Poincaré-invariant state called the vacuum
Vacuum state
In quantum field theory, the vacuum state is the quantum state with the lowest possible energy. Generally, it contains no physical particles...
and demand it is unique. Moreover, the axioms assume that the vacuum is "cyclic", i.e., that the set of all vectors which can be obtained by evaluating at the vacuum state elements of the polynomial algebra generated by the smeared field operators is a dense subset of the whole Hilbert space.
Lastly, there is the primitive causality restriction which states that any polynomial in the smeared fields can be arbitrarily accurately approximated (i.e. is the limit of operators in the weak topology
Weak topology
In mathematics, weak topology is an alternative term for initial topology. The term is most commonly used for the initial topology of a topological vector space with respect to its continuous dual...
) by polynomials over fields smeared over test functions with support in
any open subspace of Minkowski space
Minkowski space
In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
whose causal closure
Causal closure
Causal closure is a metaphysical theory about the nature of causation in the physical realm with significant ramifications in the study of the mind.-Definition:Causal closure has two main formulations - a weak and a strong form....
is the whole Minkowski space itself.
W0 (assumptions of relativistic quantum mechanics)
Quantum mechanicsQuantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
is described according to von Neumann; in particular, the pure states are given by the rays, i.e. the one-dimensional subspaces, of some separable complex Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
. In the following, the scalar product of Hilbert space vectors Ψ and Φ will be denoted by
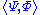, and the norm of Ψ will be denoted by 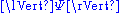. The transition probability between two pure states [Ψ] and [Φ] can be defined in terms of non-zero vector representatives Ψ and Φ to beand is independent of which representative vectors, Ψ and Φ, are chosen.
The theory of symmetry is described according to Wigner. This is to take advantage of the successful description of relativistic particles by Eugene Paul Wigner in his famous paper of 1939. See Wigner's classification
Wigner's classification
In mathematics and theoretical physics, Wigner's classificationis a classification of the nonnegative energy irreducible unitary representations of the Poincaré group, which have sharp mass eigenvalues...
. Wigner postulated that for the transition probability between states to be the same to all observers related by a transformation of special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
. More generally, he considered the statement that a theory be invariant under a group G to be expressed in terms of the invariance of the transition probability between any two rays. The statement postulates that the group acts on the set of rays, that is, on projective space. Let (a,L) be an element of the Poincaré group
Poincaré group
In physics and mathematics, the Poincaré group, named after Henri Poincaré, is the group of isometries of Minkowski spacetime.-Simple explanation:...
(the inhomogeneous Lorentz group). Thus, a is a real Lorentz four-vector
Four-vector
In the theory of relativity, a four-vector is a vector in a four-dimensional real vector space, called Minkowski space. It differs from a vector in that it can be transformed by Lorentz transformations. The usage of the four-vector name tacitly assumes that its components refer to a standard basis...
representing the change of space-time origin
where x is in the Minkowski space M4 and L is a Lorentz transformation
Lorentz transformation
In physics, the Lorentz transformation or Lorentz-Fitzgerald transformation describes how, according to the theory of special relativity, two observers' varying measurements of space and time can be converted into each other's frames of reference. It is named after the Dutch physicist Hendrik...
, which can be defined as a linear transformation of four-dimensional space-time which preserves the Lorentz distance
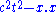of every vector 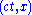. Then the theory is invariant under the Poincaré group if for every ray Ψ of the Hilbert space and every group element (a,L) is given a transformed ray Ψ(a,L)and the transition probability is unchanged by the transformation:
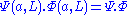
The first theorem of Wigner is that under these conditions, we can express invariance more conveniently in terms of linear or anti-linear operators (indeed, unitary
Unitary operator
In functional analysis, a branch of mathematics, a unitary operator is a bounded linear operator U : H → H on a Hilbert space H satisfyingU^*U=UU^*=I...
or antiunitary operators); the symmetry operator on the projective space of rays can be lifted to the underlying Hilbert space.
This being done for each group element (a, L), we get a family of unitary or antiunitary operators U(a, L) on our Hilbert space, such that the ray Ψ transformed by (a, L) is the same as the ray containing U(a, L) ψ. If we
restrict attention to elements of the group connected to the identity, then the anti-unitary case does not occur. Let (a, L) and (b, M) be two Poincaré transformations, and let us denote their group product by (a, L).(b,M); from the physical interpretation we see that the ray containing U(a, L)[U(b, M)]ψ must (for any psi) be the ray containing U((a, L). (b, M))ψ. Therefore these two vectors differ by a phase,
which can depend on the two group elements (a, L) and (b, M). These two vectors do not need to be equal, however. Indeed, for particles of spin 1/2, they cannot be equal for all group elements. By further use of arbitrary phase-changes, Wigner showed that the product of the representing unitary operators
Unitary representation
In mathematics, a unitary representation of a group G is a linear representation π of G on a complex Hilbert space V such that π is a unitary operator for every g ∈ G...
obeys
instead of the group law. For particles of integer spin (pions, photons, gravitons...) one can remove the +/− sign by further phase changes,
but for representations of half-odd-spin, we cannot, and the sign changes discontinuously as we go round any axis by an angle of 2π.
We can, however, construct a representation of the covering group of the Poincare group, called the inhomogeneous SL(2,C); this has elements (a, A)
where as before, a is a four-vector, but now A is a complex 2 × 2 matrix with unit determinant. We denote the unitary operator
Unitary operator
In functional analysis, a branch of mathematics, a unitary operator is a bounded linear operator U : H → H on a Hilbert space H satisfyingU^*U=UU^*=I...
s we get by U(a, A), and these give us a continuous, unitary and true representation in that the collection of U(a,A) obey the group law of the inhomogeneous SL(2,C).
Because of the sign-change under rotations by 2π, Hermitian operators transforming as spin 1/2, 3/2 etc., cannot be observable
Observable
In physics, particularly in quantum physics, a system observable is a property of the system state that can be determined by some sequence of physical operations. For example, these operations might involve submitting the system to various electromagnetic fields and eventually reading a value off...
s. This shows up as the univalence superselection
Superselection
In Quantum mechanics, superselection extends the concept of selection rules.Superselection rules are postulated rules forbidding the preparation of quantum states that exhibit coherence between eigenstates of certain observables....
rule: phases between states of spin 0, 1, 2 etc. and those of spin 1/2, 3/2 etc., are not observable. This rule is in addition to the non-observability of the overall phase of a state vector.
Concerning the observables, and states |v), we get a
representation U(a, L) of Poincaré group
Poincaré group
In physics and mathematics, the Poincaré group, named after Henri Poincaré, is the group of isometries of Minkowski spacetime.-Simple explanation:...
, on integer spin subspaces, and U(a, A) of the inhomogeneous SL(2,C) on half-odd-integer subspaces, which acts according to the following interpretation:
An ensemble corresponding to U(a, L)|v) is to be interpreted with respect to the coordinates
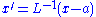in exactly the same way as an ensemble corresponding to |v) is interpreted with respect to the coordinates x; and similarly for the odd subspaces.The group of space-time translations is commutative, and so the operators can be simultaneously diagonalised. The generators of these groups give us four self-adjoint operator
Self-adjoint operator
In mathematics, on a finite-dimensional inner product space, a self-adjoint operator is an operator that is its own adjoint, or, equivalently, one whose matrix is Hermitian, where a Hermitian matrix is one which is equal to its own conjugate transpose...
s,
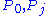, j = 1, 2, 3, which transform under the homogeneous group as a four-vector, called the energy-momentum four-vector.The second part of the zeroth axiom of Wightman is that the representation U(a, A) fulfills the spectral condition - that the simultaneous spectrum of energy-momentum is contained in the forward cone:
............... - The third part of the axiom is that there is a unique state, represented by a ray in the Hilbert space, which is invariant under the action of the Poincaré group. It is called a vacuum.
W1 (assumptions on the domain and continuity of the field)
For each test function f, there exists a set of operators which, together with their adjoints, are defined on a dense subset of the Hilbert state space, containing the vacuum. The fields A are operator-valued tempered distributionTempered distribution
*Distribution *Tempered representation...
s. The Hilbert state space is spanned by the field polynomials acting on the vacuum (cyclicity condition).
W2 (transformation law of the field)
The fields are covariant under the action of Poincaré groupPoincaré group
In physics and mathematics, the Poincaré group, named after Henri Poincaré, is the group of isometries of Minkowski spacetime.-Simple explanation:...
, and they transform according to some representation S of the Lorentz group
Lorentz group
In physics , the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical setting for all physical phenomena...
, or SL(2,C) if the spin is not integer:
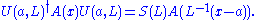
W3 (local commutativity or microscopic causality)
If the supports of two fields are space-like separated, then the fields either commute or anticommute.Cyclicity of a vacuum, and uniqueness of a vacuum are sometimes considered separately. Also, there is property of asymptotic completeness - that
Hilbert state space is spanned by the asymptotic spaces
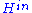and 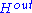, appearing in the collision S matrixS matrix
In physics, the scattering matrix relates the initial state and the final state of a physical system undergoing a scattering process...
. The other
important property of field theory is mass gap
Mass gap
In quantum field theory, the mass gap is the difference in energy between the vacuum and the next lowest energy state. The energy of the vacuum is zero by definition, and assuming that all energy states can be thought of as particles in plane-waves, the mass gap is the mass of the lightest...
which is not required by
the axioms - that energy-momentum spectrum has a gap between zero and some
positive number.
Consequences of the axioms
From these axioms, certain general theorems follow:- PCT theorem — there is general symmetry under change of parity, particle-antiparticle reversal and time inversion (none of these symmetries alone exists in nature, as it turns out)
- Connection between spinSpin (physics)In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
and statistic — fields which transform according to half integer spin anticommute, while those with integer spin commute (axiom W3) There are actually technical fine details to this theorem. This can be patched up using Klein transformations. See parastatisticsParastatisticsIn quantum mechanics and statistical mechanics, parastatistics is one of several alternatives to the better known particle statistics models...
. See also the ghosts in BRST.
Arthur Wightman
Arthur Wightman
Arthur Strong Wightman is an American mathematical physicist. He is one of the founders of the axiomatic approach to quantum field theory, and originated the set of Wightman axioms....
showed that the vacuum expectation value
Vacuum expectation value
In quantum field theory the vacuum expectation value of an operator is its average, expected value in the vacuum. The vacuum expectation value of an operator O is usually denoted by \langle O\rangle...
distributions, satisfying certain set of properties which follow from the axioms, are sufficient to reconstruct the field theory — Wightman reconstruction theorem, including the existence of a vacuum state
Vacuum state
In quantum field theory, the vacuum state is the quantum state with the lowest possible energy. Generally, it contains no physical particles...
; he did not find the condition on the vacuum expectation values guaranteeing the uniqueness of the vacuum; this condition, the cluster property
Cluster decomposition theorem
In physics, the cluster decomposition theorem guarantees locality in quantum field theory. According to this theorem, the vacuum expectation value of a product of many operators - each of them being either in region A or in region B where A and B are very separated - asymptotically equals the...
, was found later by Res Jost
Res Jost
Res Jost in Zurich) was a Swiss theoretical physicist, who worked mainly in constructive quantum field theory.-Life and work:...
, Klaus Hepp
Klaus Hepp
Klaus Hepp is a German-born Swiss theoretical physicist working mainly in quantum field theory. Hepp studied mathematics and physics at Westfälischen Wilhelms-Universität in Münster and at the Eidgenössischen Technischen Hochschule in Zurich, where, in 1962, with Res Jost as thesis first...
, David Ruelle
David Ruelle
David Pierre Ruelle is a Belgian-French mathematical physicist. He has worked on statistical physics and dynamical systems. With Floris Takens he coined the term strange attractor, and founded a new theory of turbulence...
and Othmar Steinmann.
If the theory has a mass gap
Mass gap
In quantum field theory, the mass gap is the difference in energy between the vacuum and the next lowest energy state. The energy of the vacuum is zero by definition, and assuming that all energy states can be thought of as particles in plane-waves, the mass gap is the mass of the lightest...
, i.e. there are no masses between 0 and some constant greater than zero, then vacuum expectation
Vacuum expectation value
In quantum field theory the vacuum expectation value of an operator is its average, expected value in the vacuum. The vacuum expectation value of an operator O is usually denoted by \langle O\rangle...
distributions are asymptotically independent in distant regions.
Haag's theorem
Haag's theorem
Rudolf Haag postulatedthat the interaction picture does not exist in an interacting, relativistic quantum field theory , something now commonly known as Haag's Theorem...
says that there can be no interaction picture — that we cannot use the Fock space
Fock space
The Fock space is an algebraic system used in quantum mechanics to describe quantum states with a variable or unknown number of particles. It is named after V. A...
of noninteracting particles as a Hilbert space — in the sense that we would identify Hilbert spaces via field polynomials acting on a vacuum at a certain time.
Relation to other frameworks and concepts in quantum field theory
The Wightman framework does not cover infinite energy states like finite temperature states.Unlike local quantum field theory
Local quantum field theory
The Haag-Kastler axiomatic framework for quantum field theory, named after Rudolf Haag and Daniel Kastler, is an application to local quantum physics of C*-algebra theory. It is therefore also known as Algebraic Quantum Field Theory...
, the Wightman axioms restrict the causal structure of the theory explicitly by imposing either commutativity or anticommutativity between spacelike separated fields, instead of deriving the causal structure as a theorem. If one considers a generalization of the Wightman axioms to dimensions other than 4, this (anti)commutativity postulate rules out anyon
Anyon
In physics, an anyon is a type of particle that occurs only in two-dimensional systems. It is a generalization of the fermion and boson concept.-From theory to reality:...
s and braid statistics
Braid statistics
In mathematics and theoretical physics, braid statistics is a generalization of the statistics of bosons and fermions based on the concept of braid group. A similar notion exists using a loop braid group.-See also:* Braid symmetry* Parastatistics...
in lower dimensions.
The Wightman postulate of a unique vacuum state doesn't necessarily make the Wightman axioms inappropriate for the case of spontaneous symmetry breaking
Spontaneous symmetry breaking
Spontaneous symmetry breaking is the process by which a system described in a theoretically symmetrical way ends up in an apparently asymmetric state....
because we can always restrict ourselves to a superselection sector
Superselection sector
In Quantum mechanics, superselection extends the concept of selection rules.Superselection rules are postulated rules forbidding the preparation of quantum states that exhibit coherence between eigenstates of certain observables....
.
The cyclicity of the vacuum demanded by the Wightman axioms means that they describe only the superselection sector of the vacuum; again, that is not a great loss of generality. However, this assumption does leave out finite energy states like solitons which can't be generated by a polynomial of fields smeared by test functions because a soliton, at least from a field theoretic perspective, is a global structure involving topological boundary conditions at infinity.
The Wightman framework does not cover effective field theories
Effective field theory
In physics, an effective field theory is, as any effective theory, an approximate theory, that includes appropriate degrees of freedom to describe physical phenomena occurring at a chosen length scale, while ignoring substructure and degrees of freedom at shorter distances .-The renormalization...
because there is no limit as to how small the support of a test function can be. I.e., there is no cutoff
Cutoff
In theoretical physics, cutoff is an arbitrary maximal or minimal value of energy, momentum, or length, used in order that objects with larger or smaller values than these physical quantities are ignored in some calculation...
scale.
The Wightman framework also does not cover gauge theories
Quantum gauge theory
In quantum physics, in order to quantize a gauge theory, like for example Yang-Mills theory, Chern-Simons or BF model, one method is to perform a gauge fixing. This is done in the BRST and Batalin-Vilkovisky formulation...
. Even in Abelian gauge theories conventional approaches start off with a "Hilbert space" (it's not a Hilbert space, but physicists call it a Hilbert space) with an indefinite norm and the physical states and physical operators belong to a cohomology
Cohomology
In mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
. This obviously is not covered anywhere in the Wightman framework. (However as shown by Schwinger, Christ and Lee, Gribov, Zwanziger, Van Baal, etc., canonical quantization of gauge theories in Coulomb gauge is possible with an ordinary Hilbert space, and this might be the way to make them fall under the applicability of the axiom systematics.)
The Wightman axioms can be rephrased in terms of a state called a Wightman functional on a Borchers algebra
Borchers algebra
In mathematics, a Borchers algebra or Borchers–Uhlmann algebra or BU-algebra is the tensor algebra of a vector space, often a space of smooth test functions. They were studied by , who showed that the Wightman distributions of a quantum field could be interpreted as a state, called a...
equal to the tensor algebra of a space of test functions.
Existence of theories which satisfy the axioms
One can generalize the Wightman axioms to dimensions other than 4. In dimension 2 and 3, interacting (i.e. non-free) theories which satisfy the axioms have been constructed.Currently, there is no proof that the Wightman axioms can be satisfied for interacting theories in dimension 4. In particular, the Standard model
Standard Model
The Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
of particle physics has no mathematically rigorous foundations. There is a million dollar prize for a proof that the Wightman axioms can be satisfied for gauge theories, with the additional requirement of a mass gap.
Osterwalder-Schrader reconstruction theorem
Under certain technical assumptions, it has been shown that a EuclideanEuclidean
Euclidean relates to Euclid , a town or others. It may refer to:Geometry...
QFT can be Wick-rotated
Wick rotation
In physics, Wick rotation, named after Gian-Carlo Wick, is a method of finding a solution to a mathematical problem in Minkowski space from a solution to a related problem in Euclidean space by means of a transformation that substitutes an imaginary-number variable for a real-number variable...
into a Wightman QFT. See Osterwalder-Schrader theorem. This theorem is the key tool for the constructions of interacting theories in dimension 2 and 3 which satisfy the Wightman axioms.
Literature
- R. F. StreaterRay StreaterRay F. Streater is a British physicist, and professor emeritus of Applied Mathematics at King's College London. He is best known for co-authoring a text on quantum field theory, the 1964 "PCT, Spin and Statistics and All That."- Life :...
and A. S. WightmanArthur WightmanArthur Strong Wightman is an American mathematical physicist. He is one of the founders of the axiomatic approach to quantum field theory, and originated the set of Wightman axioms....
, PCT, Spin and Statistics and All That, Princeton University Press, Landmarks in Mathematics and Physics, 2000.