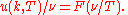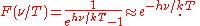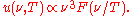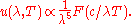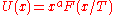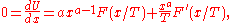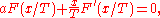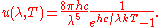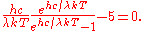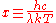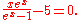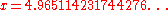
Wien's displacement law
Encyclopedia
Wavelength
In physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...
distribution of thermal radiation
Thermal radiation
Thermal radiation is electromagnetic radiation generated by the thermal motion of charged particles in matter. All matter with a temperature greater than absolute zero emits thermal radiation....
from a black body
Black body
A black body is an idealized physical body that absorbs all incident electromagnetic radiation. Because of this perfect absorptivity at all wavelengths, a black body is also the best possible emitter of thermal radiation, which it radiates incandescently in a characteristic, continuous spectrum...
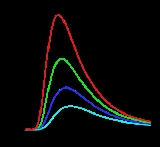
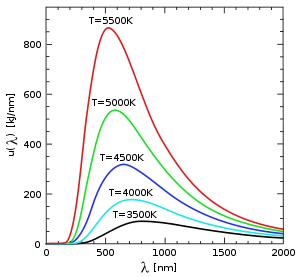
at any temperature has essentially the same shape as the distribution at any other temperature, except that each wavelength is displaced on the graph. Apart from an overall T3 multiplicative factor, the average thermal energy
Thermal energy
Thermal energy is the part of the total internal energy of a thermodynamic system or sample of matter that results in the system's temperature....
in each mode with frequency
only depends on the ratio 
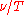. Restated in terms of the wavelength 
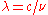, the distributions at corresponding wavelengths are related, where corresponding wavelengths are at locations proportional to 
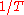. Blackbody radiation approximates to Wien's law at high frequencies.From this general law, it follows that there is an inverse relationship between the wavelength of the peak of the emission of a black body and its temperature
Temperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
when expressed as a function of wavelength, and this less powerful consequence is often also called Wien's displacement law in many textbooks.
where λmax is the peak wavelength, T is the absolute temperature of the black body, and b is a constant of proportionality called Wien's displacement constant, equal to (2002 CODATA recommended value).
For wavelengths near the visible spectrum
Visible spectrum
The visible spectrum is the portion of the electromagnetic spectrum that is visible to the human eye. Electromagnetic radiation in this range of wavelengths is called visible light or simply light. A typical human eye will respond to wavelengths from about 390 to 750 nm. In terms of...
, it is often more convenient to use the nanometer in place of the meter as the unit of measure. In this case, .
In the field of plasma physics temperatures are often measured in units of electron volts and the proportionality constant becomes .
Explanation and familiar approximate applications
The law is named for Wilhelm WienWilhelm Wien
Wilhelm Carl Werner Otto Fritz Franz Wien was a German physicist who, in 1893, used theories about heat and electromagnetism to deduce Wien's displacement law, which calculates the emission of a blackbody at any temperature from the emission at any one reference temperature.He also formulated an...
, who derived it in 1893 based on a thermodynamic argument. Wien considered adiabatic, or slow, expansion of a cavity containing waves of light in thermal equilibrium. He showed that under slow expansion or contraction, the energy of light reflecting off the walls changes in exactly the same way as the frequency. A general principle of thermodynamics is that a thermal equilibrium state, when expanded very slowly stays in thermal equilibrium. The adiabatic principle allowed Wien to conclude that for each mode, the adiabatic invariant energy/frequency is only a function of the other adiabatic invariant, the frequency/temperature.
Max Planck
Max Planck
Max Karl Ernst Ludwig Planck, ForMemRS, was a German physicist who actualized the quantum physics, initiating a revolution in natural science and philosophy. He is regarded as the founder of the quantum theory, for which he received the Nobel Prize in Physics in 1918.-Life and career:Planck came...
reinterpreted a constant
Planck constant
The Planck constant , also called Planck's constant, is a physical constant reflecting the sizes of energy quanta in quantum mechanics. It is named after Max Planck, one of the founders of quantum theory, who discovered it in 1899...
closely related to Wien's constant b as a new constant of nature, now called Planck's constant, which relates the frequency of light to the energy of a light quantum.
Wien's displacement law implies that the hotter an object is, the shorter the wavelength at which it will emit most of its radiation, and also that the wavelength for maximal or peak radiation power is found by dividing Wien's constant by the temperature in kelvins.
Examples
- Light from the Sun and Moon: The effective temperatureEffective temperatureThe effective temperature of a body such as a star or planet is the temperature of a black body that would emit the same total amount of electromagnetic radiation...
of the SunSunThe Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields...
is 5778 K. Using Wien's law, this temperature corresponds to a peak emission at a wavelength of 2.89777 million nm K/ 5778 K = 502 nm or about 5000 Å. This wavelength is fairly in the middle of the most sensitive part of land animal visual spectrum acuity. Even nocturnal animals must sense light from the moon, which is reflected sunlight with this same wavelength distribution. Also, the average wavelength of starlight maximal power is in this region, due to the sun being in the middle of a common temperature range of stars.
Wien's constant may be used in different units, and many examples to calculate familiar situation types of radiation required use of only one or two significant figures:
- Light from incandescent bulbs and fires: A lightbulb has a glowing wire with a somewhat lower temperature, resulting in yellow light, and something that is "red hot" is again a little less hot. It is easy to calculate that a wood fire at 1500 K puts out peak radiation at 3 million nm K /1500 K = 2000 nm = 20,000 Å. This is far more energy in the infrared than in the visible band, which ends about 7500 Å.
- Radiation from mammals and the living human body: Mammals at roughly 300 K emit peak radiation at 3 thousand μm K / 300 K = 10 μm, in the far infrared. This is therefore the range of infrared wavelengths that pit viper snakes and passive IR cameras must sense.
- The wavelength of radiation from the Big Bang: The blackbody radiation resulting from the Big BangBig BangThe Big Bang theory is the prevailing cosmological model that explains the early development of the Universe. According to the Big Bang theory, the Universe was once in an extremely hot and dense state which expanded rapidly. This rapid expansion caused the young Universe to cool and resulted in...
is also a typical application of Wien's law. Remembering that Wien's displacement constant is about 3 mm K, and the temperature of the Big Bang background radiation is about 3 K (actually 2.7 K), it is apparent that the microwave background of the sky peaks in power at 2.9 mm K / 2.7 K = just over 1 mm wavelength in the microwave spectrum. This provides a convenient rule of thumb for why microwave equipment must be sensitive on both sides of this frequency band, in order to do effective research on the cosmic microwave background.
weins displacement law is also given by λmax*T = constant
Frequency-dependent formulation
In terms of frequencyFrequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
(in hertzHertz
The hertz is the SI unit of frequency defined as the number of cycles per second of a periodic phenomenon. One of its most common uses is the description of the sine wave, particularly those used in radio and audio applications....
), Wien's displacement law becomes
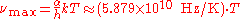
where is a constant resulting from the numerical solution of the maximization equation, k is the Boltzmann constant, h is the Planck constant
Planck constant
The Planck constant , also called Planck's constant, is a physical constant reflecting the sizes of energy quanta in quantum mechanics. It is named after Max Planck, one of the founders of quantum theory, who discovered it in 1899...
, and T is the temperature (in kelvin
Kelvin
The kelvin is a unit of measurement for temperature. It is one of the seven base units in the International System of Units and is assigned the unit symbol K. The Kelvin scale is an absolute, thermodynamic temperature scale using as its null point absolute zero, the temperature at which all...
s).
Because the spectrum from Planck's law of black body radiation
Planck's law of black body radiation
In physics, Planck's law describes the amount of energy emitted by a black body in radiation of a certain wavelength . The law is named after Max Planck, who originally proposed it in 1900. The law was the first to accurately describe black body radiation, and resolved the ultraviolet catastrophe...
takes a different shape in the frequency domain from that of the wavelength domain, the frequency location of the peak emission does not correspond to the peak wavelength using the simple relationship between frequency, wavelength, and the speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
.
Derivation
Wilhelm WienWilhelm Wien
Wilhelm Carl Werner Otto Fritz Franz Wien was a German physicist who, in 1893, used theories about heat and electromagnetism to deduce Wien's displacement law, which calculates the emission of a blackbody at any temperature from the emission at any one reference temperature.He also formulated an...
first derived this law in 1893 by applying the laws of thermodynamics
Thermodynamics
Thermodynamics is a physical science that studies the effects on material bodies, and on radiation in regions of space, of transfer of heat and of work done on or by the bodies or radiation...
to electromagnetic radiation
Electromagnetic radiation
Electromagnetic radiation is a form of energy that exhibits wave-like behavior as it travels through space...
. A modern variant of Wien's derivation can be found in the textbook by Wannier.
Wien noted that under adiabatic expansion, the energy of a mode of light, the frequency of the mode, and the total temperature of the light change together in the same way, so that their ratios are constant. This implies that in each mode at thermal equilibrium, the adiabatic invariant energy/frequency should only be a function of the adiabatic invariant frequency/temperature:
The form of F is now known from Planck's law:
Wien guessed the approximate pure exponential form, which is Wien's distribution law, a valid high frequency approximation to Planck's law. However, no matter what the function
is, the location of the peak of the distribution as a function of frequency is strictly proportional to 
.To get the usual expression for the blackbody curve, the energy per mode needs to be multiplied by the number density of modes with a given frequency
:
so that this number density is proportional to the frequency squared. The total energy per unit frequency adds the
modes together to give the total energy at frequency 
:
This per-unit-frequency expression for the density can be transformed to a per-unit-wavelength density by changing variables:
and since
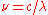, this adds a factor of 
:
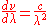These different variables only introduce a power-law in front of the function F. For any function U of the form:
the location of the maximum or minimum of U is where the derivative is zero:
which yields the trivial solution
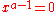and the equation:
which is an equation for
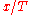, so that the minima or maxima of 
are at some definite value of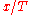 
, at an 
always strictly proportional to 
. This is the peak displacement law: the peak location is proportional to the temperature whether the density is expressed in terms of wavenumber, in terms of frequency, in terms of (1/wavelength), or in terms of any other variable where the intensity only gets multiplied by a power of this variable.The exact numerical location of the peak of the distribution depends on whether the distribution is considered per-mode-number, per-unit-frequency, or per-unit-wavelength, since the power law in front of F is different for the different forms.
Planck's law for the spectrum of black body radiation may be used to find the actual constant in the peak displacement law:
Differentiating
with respect to 
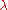and setting the derivative equal to zero gives
which can be simplified to give
When the dimensionless quantity
is defined to be
then the equation above becomes
The numerical solution to this equation is:
Solving for the wavelength
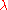in units of nanometers, and using kelvins for the temperature yields:
The frequency form of Wien's displacement law is derived using similar methods, but starting with Planck's law in terms of frequency instead of wavelength. The effective result is to substitute 3 for 5 in the equation for the peak wavelength. This is solved with x = 2.82143937212...
Using the value 4 in this equation (midway between 3 and 5) yields a "compromise" wavelength-frequency-neutral peak, which is given for x = 3.92069039487....