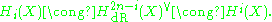Weil cohomology theory
Encyclopedia
In algebraic geometry
, a Weil cohomology or Weil cohomology theory is a cohomology satisfying certain axioms concerning the interplay of algebraic cycles and cohomology groups. The name is in honor of André Weil
. Weil cohomology theories play an important role in the theory of motives
, insofar as the category of Chow motives is a universal Weil cohomology theory in the sense that any Weil cohomology function factors through Chow motives. Note that, however, the category of Chow motives does not give a Weil cohomology theory since it is not abelian.
:
subject to the axioms below. Note that the field K is not to be confused with k; the former is a field of characteristic zero, called the coefficient field, whereas the base field k can be arbitrary. Suppose X is a smooth projective algebraic variety of dimension n, then the graded K-algebra H*(X) = ⊕Hi(X) is subject to the following:
The proofs of the axioms in the case of Betti and de Rham cohomology are comparatively easy and classical, whereas for l-adic cohomology, for example, most of the above properties are deep theorems.
The vanishing of Betti cohomology groups exceeding twice the dimension is clear from the fact that a (complex) manifold of complex dimension n has real dimension 2n, so these higher cohomology groups vanish (for example by comparing them to simplicial (co)homology
). The cycle map also has a down-to-earth explanation: given any (complex-)i-dimensional sub-variety of (the compact manifold) X of complex dimension n, one can integrate a differential (2n−i)-form along this sub-variety. The classical statement of Poincaré duality is, that this gives a non-degenerate pairing:
thus (via the comparison of de Rham cohomology and Betti cohomology) an isomorphism:
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, a Weil cohomology or Weil cohomology theory is a cohomology satisfying certain axioms concerning the interplay of algebraic cycles and cohomology groups. The name is in honor of André Weil
André Weil
André Weil was an influential mathematician of the 20th century, renowned for the breadth and quality of his research output, its influence on future work, and the elegance of his exposition. He is especially known for his foundational work in number theory and algebraic geometry...
. Weil cohomology theories play an important role in the theory of motives
Motive (algebraic geometry)
In algebraic geometry, a motive denotes 'some essential part of an algebraic variety'. To date, pure motives have been defined, while conjectural mixed motives have not. Pure motives are triples , where X is a smooth projective variety, p : X ⊢ X is an idempotent correspondence, and m an integer...
, insofar as the category of Chow motives is a universal Weil cohomology theory in the sense that any Weil cohomology function factors through Chow motives. Note that, however, the category of Chow motives does not give a Weil cohomology theory since it is not abelian.
Definition
A Weil cohomology theory is a contravariant functorFunctor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
:
-
-
-
- H*: {smooth projective varietiesAlgebraic varietyIn mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
over a field k} → {graded K-algebras}
- H*: {smooth projective varieties
-
-
subject to the axioms below. Note that the field K is not to be confused with k; the former is a field of characteristic zero, called the coefficient field, whereas the base field k can be arbitrary. Suppose X is a smooth projective algebraic variety of dimension n, then the graded K-algebra H*(X) = ⊕Hi(X) is subject to the following:
- Hi(X) are finite-dimensional K-vector spaceVector spaceA vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s. - Hi(X) vanish for i < 0 or i > 2n.
- H2n(X) is isomorphic to K (so-called orientation map).
- There is a Poincaré dualityPoincaré dualityIn mathematics, the Poincaré duality theorem named after Henri Poincaré, is a basic result on the structure of the homology and cohomology groups of manifolds...
, i.e. a non-degenerate pairing: Hi(X) × H2n−i(X) → H2n(X) ≅ K. - There is a canonical KünnethKünneth theoremIn mathematics, especially in homological algebra and algebraic topology, a Künneth theorem is a statement relating the homology of two objects to the homology of their product. The classical statement of the Künneth theorem relates the singular homology of two topological spaces X and Y and their...
isomorphism: H*(X) ⊗ H*(Y) → H*(X × Y). - There is a cycle-map: γX: Zi(X) → H2i(X), where the former group means algebraic cycles of codimension i, satisfying certain compatibility conditions with respect to functionality of H, the Künneth isomorphism and such that for X a point, the cycle map is the inclusion Z ⊂ K.
- Weak Lefschetz axiom: For any smooth hyperplane section j: W ⊂ X (i.e. W = X ∩ H, H some hyperplane in the ambient projective space), the maps j*: Hi(X) → Hi(W) are isomorphisms for i ≤ n-2 and a monomorphism for i ≤ n-1.
- Hard Lefschetz axiom: Again let W be a hyperplane section and w = γX(W) ∈ H2(X)be its image under the cycle class map. The Lefschetz operator L: Hi(X) → Hi+2(X) maps x to x·w (the dot denotes the product in the algebra H*(X)). The axiom states that Li: Hn−i(X) → Hn+i(X) is an isomorphism for i=1, ..., n.
Examples
There are four so-called classical Weil cohomology theories:- singular (=Betti) cohomology, regarding varieties over C as topological spaces using their analytic topology (see GAGAGaga- Entertainment :* Lady Gaga , American recording artist* Gaga , a dancing technique* Rara, a type of Caribbean music called Gaga in the Dominican Republic* GNZ-004 Gaga, a mobile weapon in Mobile Suit Gundam 00- Sports :...
) - de Rham cohomologyDe Rham cohomologyIn mathematics, de Rham cohomology is a tool belonging both to algebraic topology and to differential topology, capable of expressing basic topological information about smooth manifolds in a form particularly adapted to computation and the concrete representation of cohomology classes...
over a base field of characteristic zero: over C defined by differential forms and in general by means of the complex of Kähler differentials (see algebraic de Rham cohomology) - l-adic cohomologyÉtale cohomologyIn mathematics, the étale cohomology groups of an algebraic variety or scheme are algebraic analogues of the usual cohomology groups with finite coefficients of a topological space, introduced by Grothendieck in order to prove the Weil conjectures...
for varieties over fields of characteristic different from l - crystalline cohomologyCrystalline cohomologyIn mathematics, crystalline cohomology is a Weil cohomology theory for schemes introduced by and developed by . Its values are modules over rings of Witt vectors over the base field....
The proofs of the axioms in the case of Betti and de Rham cohomology are comparatively easy and classical, whereas for l-adic cohomology, for example, most of the above properties are deep theorems.
The vanishing of Betti cohomology groups exceeding twice the dimension is clear from the fact that a (complex) manifold of complex dimension n has real dimension 2n, so these higher cohomology groups vanish (for example by comparing them to simplicial (co)homology
Simplicial homology
In mathematics, in the area of algebraic topology, simplicial homology is a theory with a finitary definition, and is probably the most tangible variant of homology theory....
). The cycle map also has a down-to-earth explanation: given any (complex-)i-dimensional sub-variety of (the compact manifold) X of complex dimension n, one can integrate a differential (2n−i)-form along this sub-variety. The classical statement of Poincaré duality is, that this gives a non-degenerate pairing:
-
 ,
,
thus (via the comparison of de Rham cohomology and Betti cohomology) an isomorphism: