
Weierstrass transform
Encyclopedia
In mathematics
, the Weierstrass transform of a function
f : R → R, named after Karl Weierstrass
, is the function F defined by
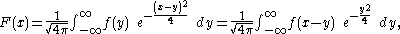
 the convolution
the convolution
of f with the Gaussian function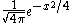 . Instead of F(x) we also write W[f](x). Note that F(x) need not exist for every real number x, because the defining integral may fail to converge.
. Instead of F(x) we also write W[f](x). Note that F(x) need not exist for every real number x, because the defining integral may fail to converge.
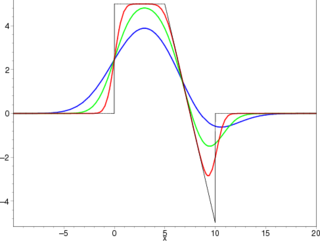
The Weierstrass transform F can be viewed as a "smoothed" version of f: the value F(x) is obtained by averaging the values of f, weighted with a Gaussian centered at x. The factor 1/√(4π
) is chosen so that the Gaussian will have a total integral of 1, with the consequence that constant functions are not changed by the Weierstrass transform.
The Weierstrass transform is intimately related to the heat equation
(or, equivalently, the diffusion equation with constant diffusion coefficient). If the function f describes the initial temperature at each point of an infinitely long rod that has constant thermal conductivity
equal to 1, then the temperature distribution of the rod t = 1 time units later will be given by the function F. By using values of t different from 1, we can define the generalized Weierstrass transform of f.
The generalized Weierstrass transform provides a means to approximate a given integrable function f arbitrarily well with analytic function
s.
and as the Hille transform after Einar Carl Hille
who studied it extensively. The generalization Wt mentioned below is known in signal analysis as a Gaussian filter
and in image processing
(when implemented on R2) as a Gaussian blur
.
is a polynomial of the same degree. Indeed, if Hn denotes the (physicist's) Hermite polynomial
of degree n, then the Weierstrass transform of Hn(x/2) is simply xn. This can be shown by exploiting the fact that the generating function
for the Hermite polynomials is closely related to the Gaussian kernel used in the definition of the Weierstrass transform.
The Weierstrass transform of the function eax (where a is an arbitrary constant) is ea2 eax. The function eax is thus an eigenvector for the Weierstrass transform. (This is in fact more generally true for all convolution transforms.) By using a=bi where i is the imaginary unit
, and using Euler's identity, we see that the Weierstrass transform of the function cos(bx) is e−b2 cos(bx) and the Weierstrass transform of the function sin(bx) is e−b2 sin(bx).
The Weierstrass transform of the function eax2 is if a < 1/4 and undefined if a ≥ 1/4. In particular, by choosing a negative, we see that the Weierstrass transform of a Gaussian function is again a Gaussian function, but a "wider" one.
if a < 1/4 and undefined if a ≥ 1/4. In particular, by choosing a negative, we see that the Weierstrass transform of a Gaussian function is again a Gaussian function, but a "wider" one.
If the transform F(x) exists for the real numbers x = a and x = b, then it also exists for all real values in between and forms an analytic function
there; moreover, F(x) will exist for all complex
values of x with a ≤ Re(x) ≤ b and forms a holomorphic function
on that strip of the complex plane
. This is the formal statement of the "smoothness" of F mentioned above.
If f is integrable over the whole real axis (i.e. f ∈ L1(R)
), then so is its Weierstrass transform F, and if furthermore f(x) ≥ 0 for all x, then also F(x) ≥ 0 for all x and the integrals of f and F are equal. This expresses the physical fact that the total thermal energy or heat
is conserved by the heat equation, or that the total amount of diffusing material is conserved by the diffusion equation.
Using the above, one can show that for 0 < p ≤ ∞ and f ∈ Lp(R)
, we have F ∈ Lp(R) and ||F||p ≤ ||f||p. The Weierstrass transform consequently yields a bounded operator
W : Lp(R) → Lp(R).
If f is sufficiently smooth, then the Weierstrass transform of the k-th derivative
of f is equal to the k-th derivative of the Weierstrass transform of f.
There is a formula relating the Weierstrass transform W and the two-sided Laplace transform
L. If we define

then
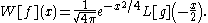
reduced by the factor e−b2. This has the consequence that higher frequencies are reduced more than lower ones, and the Weierstrass transform thus acts as a low-pass filter
. This can also be shown with the continuous Fourier transform
, as follows. The Fourier transform analyzes a signal in terms of its frequencies, transforms convolutions into products, and transforms Gaussians into Gaussians. The Weierstrass transform is convolution with a Gaussian and is therefore multiplication of the Fourier transformed signal with a Gaussian, followed by application of the inverse Fourier transform. This multiplication with a Gaussian in frequency space blends out high frequencies, which is another way of describing the "smoothing" property of the Weierstrass transform.
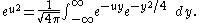
Now replace u with the formal differentiation operator D = d/dx and use the fact that formally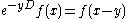 , a consequence of the Taylor series
, a consequence of the Taylor series
formula and the definition of the exponential function
.
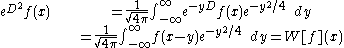
and we obtain the following formal expression for the Weierstrass transform W:
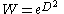
where the operator on the right is to be understood as acting on the function f(x) via

The derivation above glosses over many details of convergence, and the formula W = eD2 is therefore not universally valid; there are many functions f which have a well-defined Weierstrass transform but for which eD2f(x) cannot be meaningfully defined. Nevertheless, the rule is still quite useful and can for example be used to derive the Weierstrass transforms of polynomials, exponential and trigonometric functions mentioned above.
The formal inverse of the Weierstrass transform is thus given by

Again this formula is not universally valid but can serve as a guide. It can be shown to be correct for certain classes of functions if the right-hand side operator is properly defined.
We can also attempt to invert the Weierstrass transform in a different way: given the analytic function

we apply W−1 to obtain
once more using the (physicist's) Hermite polynomials Hn. Again, this formula for f(x) is at best formal since we didn't check whether the final series converges. But if for instance f ∈ L2(R), then knowledge of all the derivatives of F at x = 0 is enough to find the coefficients an and reconstruct f as a series of Hermite polynomials.
A third method to invert the Weierstrass transform exploits its connection to the Laplace transform mentioned above, and the well-known inversion formula for the Laplace transform. The result is stated below for distributions.
 (with some t > 0) instead of
(with some t > 0) instead of  , thus defining an operator Wt, the generalized Weierstrass transform. For small values of t, Wt[f] is very close to f, but smooth. The larger t, the more this operator averages out and changes f. Physically, Wt corresponds to following the heat (or diffusion) equation for t time units, and this is additive:
, thus defining an operator Wt, the generalized Weierstrass transform. For small values of t, Wt[f] is very close to f, but smooth. The larger t, the more this operator averages out and changes f. Physically, Wt corresponds to following the heat (or diffusion) equation for t time units, and this is additive:  corresponding to "diffusing for t time units, then s time units, is equivalent to diffusing for s + t time units". One can extend this to t = 0 by setting W0 to be the identity operator (i.e. convolution with the Dirac delta function
corresponding to "diffusing for t time units, then s time units, is equivalent to diffusing for s + t time units". One can extend this to t = 0 by setting W0 to be the identity operator (i.e. convolution with the Dirac delta function
), and these then form a one-parameter semigroup of operators.
The kernel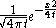 used for the generalized Weierstrass transform is sometimes called the Gauss–Weierstrass kernel, and is Green's function
used for the generalized Weierstrass transform is sometimes called the Gauss–Weierstrass kernel, and is Green's function
for the diffusion equation on R.
Wt can be computed from W: given a function f(x), define a new function ft(x) = f(x√t); then Wt[f](x) = W[ft](x/√t), a consequence of the substitution rule.
The Weierstrass transform can also be defined for certain classes of distribution
s or "generalized functions". For example, the Weierstrass transform of the Dirac delta is the Gaussian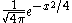 . In this context, rigorous inversion formulas can be proved, e.g.
. In this context, rigorous inversion formulas can be proved, e.g.

where x0 is any fixed real number for which F(x0) exists, the integral extends over the vertical line in the complex plane with real part x0, and the limit is to be taken in the sense of distributions.
Furthermore, the Weierstrass transform can be defined for real- (or complex-) valued functions (or distributions) defined on Rn. We use the same convolution formula as above but interpret the integral as extending over all of Rn and the expression (x − y)2 as the square of the Euclidean length
of the vector x − y; the factor in front of the integral has to be adjusted so that the Gaussian will have a total integral of 1.
More generally, the Weierstrass transform can be defined on any Riemannian manifold
: the heat equation can be formulated there (using the manifold's Laplace–Beltrami operator), and the Weierstrass transform W[f] is then given by following the solution of the heat equation for one time unit, starting with the initial "temperature distribution" f.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Weierstrass transform of a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
f : R → R, named after Karl Weierstrass
Karl Weierstrass
Karl Theodor Wilhelm Weierstrass was a German mathematician who is often cited as the "father of modern analysis".- Biography :Weierstrass was born in Ostenfelde, part of Ennigerloh, Province of Westphalia....
, is the function F defined by
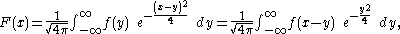

Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
of f with the Gaussian function
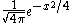 . Instead of F(x) we also write W[f](x). Note that F(x) need not exist for every real number x, because the defining integral may fail to converge.
. Instead of F(x) we also write W[f](x). Note that F(x) need not exist for every real number x, because the defining integral may fail to converge.The Weierstrass transform F can be viewed as a "smoothed" version of f: the value F(x) is obtained by averaging the values of f, weighted with a Gaussian centered at x. The factor 1/√(4π
Pi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
) is chosen so that the Gaussian will have a total integral of 1, with the consequence that constant functions are not changed by the Weierstrass transform.
The Weierstrass transform is intimately related to the heat equation
Heat equation
The heat equation is an important partial differential equation which describes the distribution of heat in a given region over time...
(or, equivalently, the diffusion equation with constant diffusion coefficient). If the function f describes the initial temperature at each point of an infinitely long rod that has constant thermal conductivity
Thermal conductivity
In physics, thermal conductivity, k, is the property of a material's ability to conduct heat. It appears primarily in Fourier's Law for heat conduction....
equal to 1, then the temperature distribution of the rod t = 1 time units later will be given by the function F. By using values of t different from 1, we can define the generalized Weierstrass transform of f.
The generalized Weierstrass transform provides a means to approximate a given integrable function f arbitrarily well with analytic function
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
s.
Names
Weierstrass used this transform in his original proof of the Weierstrass approximation theorem. It is also known as the Gauss transform or Gauss–Weierstrass transform after Carl Friedrich GaussCarl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
and as the Hille transform after Einar Carl Hille
Einar Carl Hille
Carl Einar Hille was a Swedish American mathematician.Hille was born in New York to Swedish immigrant parents. He was the son of Carl August Heuman, a civil engineer, and Edla Eckman. When Einar Hille was two years old his mother returned to Sweden and lived in Stockholm...
who studied it extensively. The generalization Wt mentioned below is known in signal analysis as a Gaussian filter
Gaussian filter
In electronics and signal processing, a Gaussian filter is a filter whose impulse response is a Gaussian function. Gaussian filters are designed to give no overshoot to a step function input while minimizing the rise and fall time. This behavior is closely connected to the fact that the Gaussian...
and in image processing
Image processing
In electrical engineering and computer science, image processing is any form of signal processing for which the input is an image, such as a photograph or video frame; the output of image processing may be either an image or, a set of characteristics or parameters related to the image...
(when implemented on R2) as a Gaussian blur
Gaussian blur
A Gaussian blur is the result of blurring an image by a Gaussian function. It is a widely used effect in graphics software, typically to reduce image noise and reduce detail...
.
Transforms of some important functions
As mentioned above, every constant function is its own Weierstrass transform. The Weierstrass transform of any polynomialPolynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
is a polynomial of the same degree. Indeed, if Hn denotes the (physicist's) Hermite polynomial
Hermite polynomials
In mathematics, the Hermite polynomials are a classical orthogonal polynomial sequence that arise in probability, such as the Edgeworth series; in combinatorics, as an example of an Appell sequence, obeying the umbral calculus; in numerical analysis as Gaussian quadrature; and in physics, where...
of degree n, then the Weierstrass transform of Hn(x/2) is simply xn. This can be shown by exploiting the fact that the generating function
Generating function
In mathematics, a generating function is a formal power series in one indeterminate, whose coefficients encode information about a sequence of numbers an that is indexed by the natural numbers. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general...
for the Hermite polynomials is closely related to the Gaussian kernel used in the definition of the Weierstrass transform.
The Weierstrass transform of the function eax (where a is an arbitrary constant) is ea2 eax. The function eax is thus an eigenvector for the Weierstrass transform. (This is in fact more generally true for all convolution transforms.) By using a=bi where i is the imaginary unit
Imaginary unit
In mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...
, and using Euler's identity, we see that the Weierstrass transform of the function cos(bx) is e−b2 cos(bx) and the Weierstrass transform of the function sin(bx) is e−b2 sin(bx).
The Weierstrass transform of the function eax2 is
 if a < 1/4 and undefined if a ≥ 1/4. In particular, by choosing a negative, we see that the Weierstrass transform of a Gaussian function is again a Gaussian function, but a "wider" one.
if a < 1/4 and undefined if a ≥ 1/4. In particular, by choosing a negative, we see that the Weierstrass transform of a Gaussian function is again a Gaussian function, but a "wider" one.General properties
The Weierstrass transform assigns to each function f a new function F; this assignment is linear. It is also translation-invariant, meaning that the transform of the function f(x + a) is F(x + a). Both of these facts are more generally true for any integral transform defined via convolution.If the transform F(x) exists for the real numbers x = a and x = b, then it also exists for all real values in between and forms an analytic function
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
there; moreover, F(x) will exist for all complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
values of x with a ≤ Re(x) ≤ b and forms a holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
on that strip of the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
. This is the formal statement of the "smoothness" of F mentioned above.
If f is integrable over the whole real axis (i.e. f ∈ L1(R)
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
), then so is its Weierstrass transform F, and if furthermore f(x) ≥ 0 for all x, then also F(x) ≥ 0 for all x and the integrals of f and F are equal. This expresses the physical fact that the total thermal energy or heat
Heat
In physics and thermodynamics, heat is energy transferred from one body, region, or thermodynamic system to another due to thermal contact or thermal radiation when the systems are at different temperatures. It is often described as one of the fundamental processes of energy transfer between...
is conserved by the heat equation, or that the total amount of diffusing material is conserved by the diffusion equation.
Using the above, one can show that for 0 < p ≤ ∞ and f ∈ Lp(R)
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
, we have F ∈ Lp(R) and ||F||p ≤ ||f||p. The Weierstrass transform consequently yields a bounded operator
Bounded operator
In functional analysis, a branch of mathematics, a bounded linear operator is a linear transformation L between normed vector spaces X and Y for which the ratio of the norm of L to that of v is bounded by the same number, over all non-zero vectors v in X...
W : Lp(R) → Lp(R).
If f is sufficiently smooth, then the Weierstrass transform of the k-th derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of f is equal to the k-th derivative of the Weierstrass transform of f.
There is a formula relating the Weierstrass transform W and the two-sided Laplace transform
Two-sided Laplace transform
In mathematics, the two-sided Laplace transform or bilateral Laplace transform is an integral transform closely related to the Fourier transform, the Mellin transform, and the ordinary or one-sided Laplace transform...
L. If we define

then
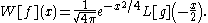
Low-pass filter
We have seen above that the Weierstrass transform of cos(bx) is e−b2 cos(bx), and analogously for sin(bx). In terms of signal analysis, this suggests that if the signal f contains the frequency b (i.e. contains a summand which is a combination of sin(bx) and cos(bx)), then the transformed signal F will contain the same frequency, but with an amplitudeAmplitude
Amplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation...
reduced by the factor e−b2. This has the consequence that higher frequencies are reduced more than lower ones, and the Weierstrass transform thus acts as a low-pass filter
Low-pass filter
A low-pass filter is an electronic filter that passes low-frequency signals but attenuates signals with frequencies higher than the cutoff frequency. The actual amount of attenuation for each frequency varies from filter to filter. It is sometimes called a high-cut filter, or treble cut filter...
. This can also be shown with the continuous Fourier transform
Continuous Fourier transform
The Fourier transform is a mathematical operation that decomposes a function into its constituent frequencies, known as a frequency spectrum. For instance, the transform of a musical chord made up of pure notes is a mathematical representation of the amplitudes of the individual notes that make...
, as follows. The Fourier transform analyzes a signal in terms of its frequencies, transforms convolutions into products, and transforms Gaussians into Gaussians. The Weierstrass transform is convolution with a Gaussian and is therefore multiplication of the Fourier transformed signal with a Gaussian, followed by application of the inverse Fourier transform. This multiplication with a Gaussian in frequency space blends out high frequencies, which is another way of describing the "smoothing" property of the Weierstrass transform.
The inverse
The following formula, closely related to the Laplace transform of a Gaussian function, is relatively easy to establish: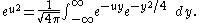
Now replace u with the formal differentiation operator D = d/dx and use the fact that formally
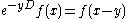 , a consequence of the Taylor series
, a consequence of the Taylor seriesTaylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
formula and the definition of the exponential function
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
.
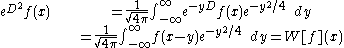
and we obtain the following formal expression for the Weierstrass transform W:
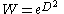
where the operator on the right is to be understood as acting on the function f(x) via

The derivation above glosses over many details of convergence, and the formula W = eD2 is therefore not universally valid; there are many functions f which have a well-defined Weierstrass transform but for which eD2f(x) cannot be meaningfully defined. Nevertheless, the rule is still quite useful and can for example be used to derive the Weierstrass transforms of polynomials, exponential and trigonometric functions mentioned above.
The formal inverse of the Weierstrass transform is thus given by

Again this formula is not universally valid but can serve as a guide. It can be shown to be correct for certain classes of functions if the right-hand side operator is properly defined.
We can also attempt to invert the Weierstrass transform in a different way: given the analytic function

we apply W−1 to obtain
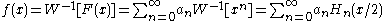
once more using the (physicist's) Hermite polynomials Hn. Again, this formula for f(x) is at best formal since we didn't check whether the final series converges. But if for instance f ∈ L2(R), then knowledge of all the derivatives of F at x = 0 is enough to find the coefficients an and reconstruct f as a series of Hermite polynomials.
A third method to invert the Weierstrass transform exploits its connection to the Laplace transform mentioned above, and the well-known inversion formula for the Laplace transform. The result is stated below for distributions.
Generalizations
We can use convolution with the Gaussian kernel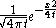 (with some t > 0) instead of
(with some t > 0) instead of 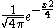 , thus defining an operator Wt, the generalized Weierstrass transform. For small values of t, Wt[f] is very close to f, but smooth. The larger t, the more this operator averages out and changes f. Physically, Wt corresponds to following the heat (or diffusion) equation for t time units, and this is additive:
, thus defining an operator Wt, the generalized Weierstrass transform. For small values of t, Wt[f] is very close to f, but smooth. The larger t, the more this operator averages out and changes f. Physically, Wt corresponds to following the heat (or diffusion) equation for t time units, and this is additive: 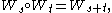 corresponding to "diffusing for t time units, then s time units, is equivalent to diffusing for s + t time units". One can extend this to t = 0 by setting W0 to be the identity operator (i.e. convolution with the Dirac delta function
corresponding to "diffusing for t time units, then s time units, is equivalent to diffusing for s + t time units". One can extend this to t = 0 by setting W0 to be the identity operator (i.e. convolution with the Dirac delta functionDirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
), and these then form a one-parameter semigroup of operators.
The kernel
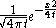 used for the generalized Weierstrass transform is sometimes called the Gauss–Weierstrass kernel, and is Green's function
used for the generalized Weierstrass transform is sometimes called the Gauss–Weierstrass kernel, and is Green's functionGreen's function
In mathematics, a Green's function is a type of function used to solve inhomogeneous differential equations subject to specific initial conditions or boundary conditions...
for the diffusion equation on R.
Wt can be computed from W: given a function f(x), define a new function ft(x) = f(x√t); then Wt[f](x) = W[ft](x/√t), a consequence of the substitution rule.
The Weierstrass transform can also be defined for certain classes of distribution
Distribution (mathematics)
In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
s or "generalized functions". For example, the Weierstrass transform of the Dirac delta is the Gaussian
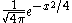 . In this context, rigorous inversion formulas can be proved, e.g.
. In this context, rigorous inversion formulas can be proved, e.g.
where x0 is any fixed real number for which F(x0) exists, the integral extends over the vertical line in the complex plane with real part x0, and the limit is to be taken in the sense of distributions.
Furthermore, the Weierstrass transform can be defined for real- (or complex-) valued functions (or distributions) defined on Rn. We use the same convolution formula as above but interpret the integral as extending over all of Rn and the expression (x − y)2 as the square of the Euclidean length
Euclidean distance
In mathematics, the Euclidean distance or Euclidean metric is the "ordinary" distance between two points that one would measure with a ruler, and is given by the Pythagorean formula. By using this formula as distance, Euclidean space becomes a metric space...
of the vector x − y; the factor in front of the integral has to be adjusted so that the Gaussian will have a total integral of 1.
More generally, the Weierstrass transform can be defined on any Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
: the heat equation can be formulated there (using the manifold's Laplace–Beltrami operator), and the Weierstrass transform W[f] is then given by following the solution of the heat equation for one time unit, starting with the initial "temperature distribution" f.

