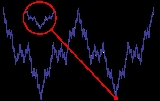
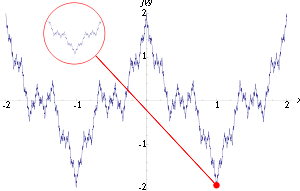
Weierstrass function
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Weierstrass function is a pathological
Pathological (mathematics)
In mathematics, a pathological phenomenon is one whose properties are considered atypically bad or counterintuitive; the opposite is well-behaved....
example of a real-valued function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
on the real line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
. The function has the property that it is continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
everywhere but differentiable nowhere. It is named after its discoverer Karl Weierstrass
Karl Weierstrass
Karl Theodor Wilhelm Weierstrass was a German mathematician who is often cited as the "father of modern analysis".- Biography :Weierstrass was born in Ostenfelde, part of Ennigerloh, Province of Westphalia....
.
Historically, the Weierstrass function is important because it was the first published (1872) to challenge the notion that every continuous function was differentiable except on a set of isolated points.
Construction
In Weierstrass' original paper, the function was defined by
where
, 
is a positive odd integer, and
This construction, along with the proof that it is nowhere differentiable, was first given by Weierstrass in a paper presented to the Königliche Akademie der Wissenschaften
Prussian Academy of Sciences
The Prussian Academy of Sciences was an academy established in Berlin on 11 July 1700, four years after the Akademie der Künste or "Arts Academy", to which "Berlin Academy" may also refer.-Origins:...
on 18 July 1872.
The proof that this function is continuous everywhere is not difficult. Since the terms of the infinite series which defines it are bounded by
and this has finite sum for 
, convergence of the sum of the terms is uniform by the Weierstrass M-test with 
. Since each partial sum is continuous and the uniform limit of continuous functions is continuous, 
is continuous.To prove that it is nowhere differentiable, we consider an arbitrary point
and show that the function is not differentiable at that point. To do this, we construct two sequences of points 
and 
which both converge to x, having the property that
Naively it might be expected that a continuous function must have a derivative, or that the set of points where it is not differentiable should be "small" in some sense. According to Weierstrass in his paper, earlier mathematicians including Gauss
Carl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
had often assumed that this was true. This might be because it is difficult to draw or visualise a continuous function whose set of nondifferentiable points is something other than a finite set of points. Analogous results for better behaved classes of continuous functions do exist, for example the Lipschitz functions, whose set of non-differentiability points must be a Lebesgue null set (Rademacher's theorem
Rademacher's theorem
In mathematical analysis, Rademacher's theorem, named after Hans Rademacher, states the following: If U is an open subset of Rn andis Lipschitz continuous, then f is Fréchet-differentiable almost everywhere in U In mathematical analysis, Rademacher's theorem, named after Hans Rademacher, states the...
). When we try to draw a general continuous function, we usually draw the graph of a function which is Lipschitz and has other nice properties.
The Weierstrass function could perhaps be described as one of the very first fractals studied, although this term was not used until much later. The function has detail at every level, so zooming in on a piece of the curve does not show it getting progressively closer and closer to a straight line. Rather between any two points no matter how close, the function will not be monotone. The Hausdorff dimension
Hausdorff dimension
thumb|450px|Estimating the Hausdorff dimension of the coast of Great BritainIn mathematics, the Hausdorff dimension is an extended non-negative real number associated with any metric space. The Hausdorff dimension generalizes the notion of the dimension of a real vector space...
of the classical Weierstrass function is bounded above by
, (where a and b are the constants in the construction above) and is generally believed to be exactly that value, but this had not been proven rigorously.The term Weierstrass function is often used in real analysis to refer to any function with similar properties and construction to Weierstrass' original example. For example, the cosine function can be replaced in the infinite series by a piecewise linear "zigzag" function
Triangle wave
A triangle wave is a non-sinusoidal waveform named for its triangular shape.Like a square wave, the triangle wave contains only odd harmonics...
. G. H. Hardy
G. H. Hardy
Godfrey Harold “G. H.” Hardy FRS was a prominent English mathematician, known for his achievements in number theory and mathematical analysis....
showed that the function of the above construction is nowhere differentiable with the assumptions
.Hölder continuity
It is convenient to write the Weierstrass function equivalently as
for some . Then Wα(x) is Hölder continuous of exponent α, which is to say that there is a constant C such that
for all x and y. Moreover, W1 Hölder continuous of all orders but not Lipschitz continuous.
Density of nowhere-differentiable functions
It turns out that the Weierstrass function is far from being an isolated example: although it is "pathological", it is also "typical" of continuous functions:- In a topologicalTopologyTopology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
sense: the set of nowhere-differentiable real-valued functions on [0, 1] is comeager in the vector spaceVector spaceA vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
C([0, 1]; R) of all continuous real-valued functions on [0, 1] with the topology of uniform convergence. - In a measure-theoretic sense: when the space C([0, 1]; R) is equipped with classical Wiener measure γ, the collection of functions that are differentiable at even a single point of [0, 1] has γ-measure zero. The same is true even if one takes finite-dimensional "slices" of C([0, 1]; R): the nowhere-differentiable functions form a prevalent subsetPrevalent and shy setsIn mathematics, the notions of prevalence and shyness are notions of "almost everywhere" and "measure zero" that are well-suited to the study of infinite-dimensional spaces and make use of the translation-invariant Lebesgue measure on finite-dimensional real spaces...
of C([0, 1]; R).
External links
(a different Weierstrass Function which is also continuous and nowhere differentiable)- Nowhere differentiable continuous function proof of existence using Banach's contraction principle.
- Nowhere monotonic continuous function proof of existence using the Baire category theoremBaire category theoremThe Baire category theorem is an important tool in general topology and functional analysis. The theorem has two forms, each of which gives sufficient conditions for a topological space to be a Baire space....
. - Weierstrass function in the complex plane Beautiful fractal.
- SpringerLink - Journal of Fourier Analysis and Applications, Volume 16, Number 1 Simple Proofs of Nowhere-Differentiability for Weierstrass’s Function and Cases of Slow Growth