
Von Neumann–Bernays–Gödel set theory
Encyclopedia
In the foundations of mathematics
, von Neumann–Bernays–Gödel set theory (NBG) is an axiomatic set theory that is a conservative extension
of the canonical axiomatic set theory ZFC. A statement in the language of ZFC is provable in NBG if and only if
it is provable in ZFC. The ontology
of NBG includes proper classes, objects having members but that cannot be members of other entities. NBG's principle of class comprehension is predicative
; quantified variables in the defining formula can range only over sets. Allowing impredicative
comprehension turns NBG into Morse-Kelley set theory (MK). NBG, unlike ZFC and MK, can be finitely axiomatized.
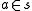 is defined if a is a set and s is a class
is defined if a is a set and s is a class
. In other words,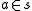 is defined unless a is a proper class. A proper class is very large; NBG even admits of "the class of all sets", the universal class called V. However, NBG does not admit "the class of all classes" (which fails because proper classes are not "objects" that can be put into classes in NBG) or "the set of all sets" (whose existence cannot be justified with NBG axioms).
is defined unless a is a proper class. A proper class is very large; NBG even admits of "the class of all sets", the universal class called V. However, NBG does not admit "the class of all classes" (which fails because proper classes are not "objects" that can be put into classes in NBG) or "the set of all sets" (whose existence cannot be justified with NBG axioms).
By NBG's axiom schema of Class Comprehension, all objects satisfying any given formula in the first order language of NBG form a class; if the class would not be a set in ZFC, it is an NBG proper class.
The development of classes mirrors the development of naive set theory
. The principle of abstraction is given, and thus classes can be formed out of all individuals satisfying any statement of first order logic whose atomic sentence
s all involve either the membership relation or predicates definable from membership. Equality, pairing, subclass, and such, are all definable and so need not be axiomatized — their definitions denote a particular abstraction
of a formula
.
Sets are developed in a manner very similarly to ZF. Let Rp(A,a), meaning "the set a represents the class A," denote a binary relation
defined as follows:
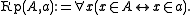
That is, a "represents" A if every element of a is an element of A, and conversely. Classes lacking representations, such as the class of all sets that do not contain themselves (the class invoked by the Russell paradox), are the proper classes.
in the 1920s, took functions
and not sets, as primitive. In a series of articles published 1937-54, Paul Bernays
modified Von Neumann's theory so as to make sets and set membership primitive; he also discovered that it could be finitely axiomatized. Gödel
(1940), while investigating the independence of the Continuum hypothesis
, further simplified and used the theory. Montague
(1961) showed that ZFC cannot be finitely axiomatized.
 " should be read "set x is a member of set y," and "
" should be read "set x is a member of set y," and "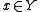 " as "set x is a member of class Y." Statements of equality may take the form
" as "set x is a member of class Y." Statements of equality may take the form
"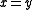 " or "
" or "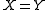 ". "
". "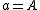 " stands for "
" stands for "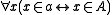 " and is an abuse of notation
" and is an abuse of notation
. NBG can also be presented as a one-sorted theory of classes, with sets being those classes that are members of at least one other class.
We first axiomatize NBG using the . This schema is provably equivalent to 9 of its finite instances, stated in the following section. Hence these 9 finite axioms can replace Class Comprehension. This is the precise sense in which NBG can be finitely axiomatized.
The remaining axioms have capitalized names because they are primarily concerned with classes rather than sets. The next two axioms differ from their ZFC counterparts only in that their quantified variables range over classes, not sets:
The last two axioms are peculiar to NBG:
We develop our axiomatization by considering the structure of formulas.
This axiom, in combination with the set existence axioms from the previous axiomatization, assures the existence of classes from the outset, and enables formulas with class parameters.
Let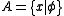 and
and 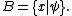 Then
Then  and
and 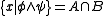 suffice for handling all sentential connectives, because ∧ and ¬ are a functionally complete set of connectives.
suffice for handling all sentential connectives, because ∧ and ¬ are a functionally complete set of connectives.
We now turn to quantification. In order to handle multiple variables, we need the ability to represent relations
. Define the ordered pair
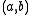 as
as 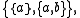 as usual. Note that two applications of pairing to a and b assure that (a,b) is indeed a set.
as usual. Note that two applications of pairing to a and b assure that (a,b) is indeed a set.
These axioms license adding dummy arguments, and rearranging the order of arguments, in relations of any arity
. The peculiar form of Association is designed exactly to make it possible to bring any term in a list of arguments to the front (with the help of Converses). We represent the argument list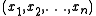 as
as 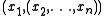 (it is a pair with the first argument as its first projection and the "tail" of the argument list as the second projection). The idea is to apply Assoc1 until the argument to be brought to the front is second, then apply Conv1 or Conv2 as appropriate to bring the second argument to the front, then apply Assoc2 until the effects of the original applications of Assoc1 (which are now behind the moved argument) are corrected.
(it is a pair with the first argument as its first projection and the "tail" of the argument list as the second projection). The idea is to apply Assoc1 until the argument to be brought to the front is second, then apply Conv1 or Conv2 as appropriate to bring the second argument to the front, then apply Assoc2 until the effects of the original applications of Assoc1 (which are now behind the moved argument) are corrected.
If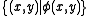 is a class considered as a relation, then its range
is a class considered as a relation, then its range
,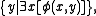 is a class. This gives us the existential quantifier. The universal quantifier can be defined in terms of the existential quantifier and negation
is a class. This gives us the existential quantifier. The universal quantifier can be defined in terms of the existential quantifier and negation
.
The above axioms can reorder the arguments of any relation so as to bring any desired argument to the front of the argument list, where it can be quantified.
Finally, each atomic formula
implies the existence of a corresponding class relation:
Diagonal, together with addition of dummy arguments and rearrangement of arguments, can build a relation asserting the equality of any two of its arguments; thus repeated variables can be handled.
B6 and B7 enable what Converses and Association enable: given any class X of ordered triples, there exists another class Y whose members are the members of X each reordered in the same way.
and other philosophical issues posed by NBG, especially when contrasted with ZFC and MK
, see Appendix C of Potter (2004).
Even though NBG is a conservative extension
of ZFC, a theorem may have a shorter and more elegant proof in NBG than in ZFC (or vice versa). For a survey of known results of this nature, see Pudlak (1998).
of ZFC and the von Neumann universe
. Now let the members of V include the inaccessible cardinal
κ. Also let Def(X) denote the Δ0 definable subset
s of X (see constructible universe
). Then:
, for instance, a "large category" is defined as one whose objects make up a proper class, with the same being true of its morphism
s. A "small category", on the other hand, is one whose objects and morphisms are members of some set. We can thus easily speak of the "category of all sets" or "category of all small categories" without risking paradox. Those categories are large, of course. There is no "category of all categories" since it would have to contain the category of small categories, although yet another ontological extension can enable one to talk formally about such a "category" (see for example the "quasicategory of all categories" of Adámek et al. (1990), whose objects and morphisms form a "proper conglomerate").
On whether an ontology including classes as well as sets is adequate for category theory
, see Muller (2001).
Foundations of mathematics
Foundations of mathematics is a term sometimes used for certain fields of mathematics, such as mathematical logic, axiomatic set theory, proof theory, model theory, type theory and recursion theory...
, von Neumann–Bernays–Gödel set theory (NBG) is an axiomatic set theory that is a conservative extension
Conservative extension
In mathematical logic, a logical theory T_2 is a conservative extension of a theory T_1 if the language of T_2 extends the language of T_1; every theorem of T_1 is a theorem of T_2; and any theorem of T_2 which is in the language of T_1 is already a theorem of T_1.More generally, if Γ is a set of...
of the canonical axiomatic set theory ZFC. A statement in the language of ZFC is provable in NBG if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
it is provable in ZFC. The ontology
Ontology
Ontology is the philosophical study of the nature of being, existence or reality as such, as well as the basic categories of being and their relations...
of NBG includes proper classes, objects having members but that cannot be members of other entities. NBG's principle of class comprehension is predicative
Impredicative
In mathematics and logic, impredicativity is the property of a self-referencing definition. More precisely, a definition is said to be impredicative if it invokes the set being defined, or another set which contains the thing being defined.Russell's paradox is a famous example of an impredicative...
; quantified variables in the defining formula can range only over sets. Allowing impredicative
Impredicative
In mathematics and logic, impredicativity is the property of a self-referencing definition. More precisely, a definition is said to be impredicative if it invokes the set being defined, or another set which contains the thing being defined.Russell's paradox is a famous example of an impredicative...
comprehension turns NBG into Morse-Kelley set theory (MK). NBG, unlike ZFC and MK, can be finitely axiomatized.
Ontology
The defining aspect of NBG is the distinction between proper class and set. Let a and s be two individuals. Then the atomic sentenceAtomic sentence
In logic, an atomic sentence is a type of declarative sentence which is either true or false and which cannot be broken down into other simpler sentences...
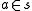 is defined if a is a set and s is a class
is defined if a is a set and s is a classClass (set theory)
In set theory and its applications throughout mathematics, a class is a collection of sets which can be unambiguously defined by a property that all its members share. The precise definition of "class" depends on foundational context...
. In other words,
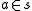 is defined unless a is a proper class. A proper class is very large; NBG even admits of "the class of all sets", the universal class called V. However, NBG does not admit "the class of all classes" (which fails because proper classes are not "objects" that can be put into classes in NBG) or "the set of all sets" (whose existence cannot be justified with NBG axioms).
is defined unless a is a proper class. A proper class is very large; NBG even admits of "the class of all sets", the universal class called V. However, NBG does not admit "the class of all classes" (which fails because proper classes are not "objects" that can be put into classes in NBG) or "the set of all sets" (whose existence cannot be justified with NBG axioms).By NBG's axiom schema of Class Comprehension, all objects satisfying any given formula in the first order language of NBG form a class; if the class would not be a set in ZFC, it is an NBG proper class.
The development of classes mirrors the development of naive set theory
Naive set theory
Naive set theory is one of several theories of sets used in the discussion of the foundations of mathematics. The informal content of this naive set theory supports both the aspects of mathematical sets familiar in discrete mathematics , and the everyday usage of set theory concepts in most...
. The principle of abstraction is given, and thus classes can be formed out of all individuals satisfying any statement of first order logic whose atomic sentence
Atomic sentence
In logic, an atomic sentence is a type of declarative sentence which is either true or false and which cannot be broken down into other simpler sentences...
s all involve either the membership relation or predicates definable from membership. Equality, pairing, subclass, and such, are all definable and so need not be axiomatized — their definitions denote a particular abstraction
Abstraction
Abstraction is a process by which higher concepts are derived from the usage and classification of literal concepts, first principles, or other methods....
of a formula
Formula
In mathematics, a formula is an entity constructed using the symbols and formation rules of a given logical language....
.
Sets are developed in a manner very similarly to ZF. Let Rp(A,a), meaning "the set a represents the class A," denote a binary relation
Binary relation
In mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
defined as follows:
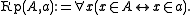
That is, a "represents" A if every element of a is an element of A, and conversely. Classes lacking representations, such as the class of all sets that do not contain themselves (the class invoked by the Russell paradox), are the proper classes.
History
The first variant of NBG, by John von NeumannJohn von Neumann
John von Neumann was a Hungarian-American mathematician and polymath who made major contributions to a vast number of fields, including set theory, functional analysis, quantum mechanics, ergodic theory, geometry, fluid dynamics, economics and game theory, computer science, numerical analysis,...
in the 1920s, took functions
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
and not sets, as primitive. In a series of articles published 1937-54, Paul Bernays
Paul Bernays
Paul Isaac Bernays was a Swiss mathematician, who made significant contributions to mathematical logic, axiomatic set theory, and the philosophy of mathematics. He was an assistant to, and close collaborator of, David Hilbert.-Biography:Bernays spent his childhood in Berlin. Bernays attended the...
modified Von Neumann's theory so as to make sets and set membership primitive; he also discovered that it could be finitely axiomatized. Gödel
Kurt Gödel
Kurt Friedrich Gödel was an Austrian logician, mathematician and philosopher. Later in his life he emigrated to the United States to escape the effects of World War II. One of the most significant logicians of all time, Gödel made an immense impact upon scientific and philosophical thinking in the...
(1940), while investigating the independence of the Continuum hypothesis
Continuum hypothesis
In mathematics, the continuum hypothesis is a hypothesis, advanced by Georg Cantor in 1874, about the possible sizes of infinite sets. It states:Establishing the truth or falsehood of the continuum hypothesis is the first of Hilbert's 23 problems presented in the year 1900...
, further simplified and used the theory. Montague
Richard Montague
Richard Merett Montague was an American mathematician and philosopher.-Career:At the University of California, Berkeley, Montague earned an B.A. in Philosophy in 1950, an M.A. in Mathematics in 1953, and a Ph.D. in Philosophy 1957, the latter under the direction of the mathematician and logician...
(1961) showed that ZFC cannot be finitely axiomatized.
Axiomatizating NBG
NBG is presented here as a two-sorted theory, with lower case letters denoting variables ranging over sets, and upper case letters denoting variables ranging over classes. Hence " " should be read "set x is a member of set y," and "
" should be read "set x is a member of set y," and "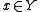 " as "set x is a member of class Y." Statements of equality may take the form
" as "set x is a member of class Y." Statements of equality may take the form"
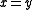 " or "
" or "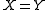 ". "
". "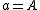 " stands for "
" stands for "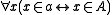 " and is an abuse of notation
" and is an abuse of notationAbuse of notation
In mathematics, abuse of notation occurs when an author uses a mathematical notation in a way that is not formally correct but that seems likely to simplify the exposition or suggest the correct intuition . Abuse of notation should be contrasted with misuse of notation, which should be avoided...
. NBG can also be presented as a one-sorted theory of classes, with sets being those classes that are members of at least one other class.
We first axiomatize NBG using the . This schema is provably equivalent to 9 of its finite instances, stated in the following section. Hence these 9 finite axioms can replace Class Comprehension. This is the precise sense in which NBG can be finitely axiomatized.
With Class Comprehension schema
The following five axioms are identical to their ZFC counterparts:- extensionality:
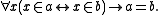 : Sets with the same elements are the same set.
: Sets with the same elements are the same set. - pairingAxiom of pairingIn axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of pairing is one of the axioms of Zermelo–Fraenkel set theory.- Formal statement :...
: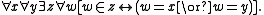 For any sets x and y, there is a set,
For any sets x and y, there is a set, 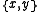 , whose elements are exactly x and y.
, whose elements are exactly x and y.
- pairing implies that for any set x, the set {x} (the singleton set) exists. Also, given any two sets x and y and the usual set-theoretic definition of the ordered pairOrdered pairIn mathematics, an ordered pair is a pair of mathematical objects. In the ordered pair , the object a is called the first entry, and the object b the second entry of the pair...
, the ordered pair (x,y) exists and is a set. By Class Comprehension, all relations on sets are classes. Moreover, certain kinds class relations are one or more of functions, injections, and bijections from one class to another. pairing is an axiom in Zermelo set theoryZermelo set theoryZermelo set theory, as set out in an important paper in 1908 by Ernst Zermelo, is the ancestor of modern set theory. It bears certain differences from its descendants, which are not always understood, and are frequently misquoted...
and a theorem in ZFC.
- unionAxiom of unionIn axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of union is one of the axioms of Zermelo-Fraenkel set theory, stating that, for any set x there is a set y whose elements are precisely the elements of the elements of x...
: For any set x, there is a set which contains exactly the elements of elements of x. - power setAxiom of power setIn mathematics, the axiom of power set is one of the Zermelo–Fraenkel axioms of axiomatic set theory.In the formal language of the Zermelo–Fraenkel axioms, the axiom reads:...
: For any set x, there is a set which contains exactly the subsets of x. - infinityAxiom of infinityIn axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of infinity is one of the axioms of Zermelo-Fraenkel set theory...
: There exists an inductive setInductive setIn descriptive set theory, an inductive set of real numbers is one that can be defined as the least fixed point of a monotone operation definable by a positive Σ1n formula, for some natural number n, together with a real parameter.The inductive sets form a boldface pointclass; that is, they...
, namely a set x whose members are (i) the empty setEmpty setIn mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
; (ii) for every member y of x, is also a member of x.
is also a member of x.
- infinity can be formulated so as to imply the existence of the empty set.
The remaining axioms have capitalized names because they are primarily concerned with classes rather than sets. The next two axioms differ from their ZFC counterparts only in that their quantified variables range over classes, not sets:
- Extensionality:
 : Classes with the same elements are the same class.
: Classes with the same elements are the same class. - Foundation (Regularity): Each nonempty class is disjoint from one of its elements.
The last two axioms are peculiar to NBG:
- Limitation of SizeAxiom of limitation of sizeIn class theories, the axiom of limitation of size says that for any class C, C is a proper class, that is a class which is not a set , if and only if it can be mapped onto the class V of all sets....
: For any class C, a set x such that x=C exists if and only if there is no bijectionBijectionA bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
between C and the class V of all sets.
- From this axiom, due to Von Neumann, Subsets, ReplacementAxiom schema of replacementIn set theory, the axiom schema of replacement is a schema of axioms in Zermelo–Fraenkel set theory that asserts that the image of any set under any definable mapping is also a set...
, and Global ChoiceAxiom of global choiceIn class theories, the axiom of global choice is a stronger variant of the axiom of choice which applies to proper classes as well as sets.- Statement :The axiom can be expressed in various ways which are equivalent:...
can all be derived. This axiom implies the axiom of global choiceAxiom of global choiceIn class theories, the axiom of global choice is a stronger variant of the axiom of choice which applies to proper classes as well as sets.- Statement :The axiom can be expressed in various ways which are equivalent:...
because the class of ordinalsOrdinal numberIn set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
is not a set; hence there exists a bijectionBijectionA bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
between the ordinals and the universeVon Neumann universeIn set theory and related branches of mathematics, the von Neumann universe, or von Neumann hierarchy of sets, denoted V, is the class of hereditary well-founded sets...
. If Limitation of Size were weakened to "If the domain of a class function is a set, then the range of that function is likewise a set," then no form of the axiom of choice is an NBG theorem. In this case, any of the usual local forms of Choice may be taken as an added axiom, if desired.
- Limitation of Size cannot be found in Mendelson (1997) NGB. In its place, we find the usual axiom of choice for sets, and the following form of the axiom schema of replacementAxiom schema of replacementIn set theory, the axiom schema of replacement is a schema of axioms in Zermelo–Fraenkel set theory that asserts that the image of any set under any definable mapping is also a set...
: if the class F is a function whose domainDomain (mathematics)In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
is a set, the rangeRange (mathematics)In mathematics, the range of a function refers to either the codomain or the image of the function, depending upon usage. This ambiguity is illustrated by the function f that maps real numbers to real numbers with f = x^2. Some books say that range of this function is its codomain, the set of all...
of F is also a set .
- Class Comprehension schema: For any formula
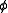 containing no quantifiers over classes (it may contain class and set parameters), there is a class A such that
containing no quantifiers over classes (it may contain class and set parameters), there is a class A such that 
- This axiom asserts that invoking the principle of unrestricted comprehensionAxiom schema of specificationIn axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom schema of specification, axiom schema of separation, subset axiom scheme or axiom schema of restricted comprehension, is a schema of axioms in Zermelo-Fraenkel set theory...
of naive set theoryNaive set theoryNaive set theory is one of several theories of sets used in the discussion of the foundations of mathematics. The informal content of this naive set theory supports both the aspects of mathematical sets familiar in discrete mathematics , and the everyday usage of set theory concepts in most...
yields a class rather than a set, thereby banishing the paradoxes of set theoryParadoxes of set theoryThis article contains a discussion of paradoxes of set theory. As with most mathematical paradoxes, they generally reveal surprising and counter-intuitive mathematical results, rather than actual logical contradictions within modern axiomatic set theory....
.
- Class Comprehension is the only axiom schema of NBG. In the next section, we show how this schema can be replaced by a number of its own instances. Hence NBG can be finitely axiomatized. If the quantified variables in φ(x) range over classes instead of sets, the result is Morse–Kelley set theoryMorse–Kelley set theoryIn the foundation of mathematics, Morse–Kelley set theory or Kelley–Morse set theory is a first order axiomatic set theory that is closely related to von Neumann–Bernays–Gödel set theory...
, a proper extension of ZFC which cannot be finitely axiomatized.
Replacing Class Comprehension with finite instances thereof
An appealing but somewhat mysterious feature of NBG is that its axiom schema of Class Comprehension is equivalent to the conjunction of a finite number of its instances. The axioms of this section may replace the Axiom Schema of Class Comprehension in the preceding section. The finite axiomatization presented below does not necessarily resemble exactly any NBG axiomatization in print.We develop our axiomatization by considering the structure of formulas.
- Sets: For any set x, there is a class X such that x=X.
This axiom, in combination with the set existence axioms from the previous axiomatization, assures the existence of classes from the outset, and enables formulas with class parameters.
Let
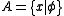 and
and 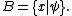 Then
Then  and
and 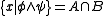 suffice for handling all sentential connectives, because ∧ and ¬ are a functionally complete set of connectives.
suffice for handling all sentential connectives, because ∧ and ¬ are a functionally complete set of connectives.- Complement: For any class A, the complementComplement (set theory)In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
 is a class.
is a class. - Intersection: For any classes A and B, the intersectionIntersection (set theory)In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
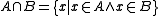 is a class.
is a class.
We now turn to quantification. In order to handle multiple variables, we need the ability to represent relations
Relation (mathematics)
In set theory and logic, a relation is a property that assigns truth values to k-tuples of individuals. Typically, the property describes a possible connection between the components of a k-tuple...
. Define the ordered pair
Ordered pair
In mathematics, an ordered pair is a pair of mathematical objects. In the ordered pair , the object a is called the first entry, and the object b the second entry of the pair...
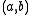 as
as 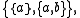 as usual. Note that two applications of pairing to a and b assure that (a,b) is indeed a set.
as usual. Note that two applications of pairing to a and b assure that (a,b) is indeed a set.- Products: For any classes A and B, the class
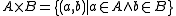 is a class. (In practice, only
is a class. (In practice, only  is needed.)
is needed.) - Converses: For any class R, the classes:
-
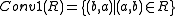 and
and -
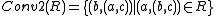 exist.
exist.
- Association: For any class R, the classes:
-
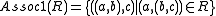 and
and -
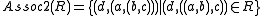 exist.
exist.
These axioms license adding dummy arguments, and rearranging the order of arguments, in relations of any arity
Arity
In logic, mathematics, and computer science, the arity of a function or operation is the number of arguments or operands that the function takes. The arity of a relation is the dimension of the domain in the corresponding Cartesian product...
. The peculiar form of Association is designed exactly to make it possible to bring any term in a list of arguments to the front (with the help of Converses). We represent the argument list
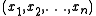 as
as 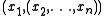 (it is a pair with the first argument as its first projection and the "tail" of the argument list as the second projection). The idea is to apply Assoc1 until the argument to be brought to the front is second, then apply Conv1 or Conv2 as appropriate to bring the second argument to the front, then apply Assoc2 until the effects of the original applications of Assoc1 (which are now behind the moved argument) are corrected.
(it is a pair with the first argument as its first projection and the "tail" of the argument list as the second projection). The idea is to apply Assoc1 until the argument to be brought to the front is second, then apply Conv1 or Conv2 as appropriate to bring the second argument to the front, then apply Assoc2 until the effects of the original applications of Assoc1 (which are now behind the moved argument) are corrected.If
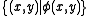 is a class considered as a relation, then its range
is a class considered as a relation, then its rangeRange (mathematics)
In mathematics, the range of a function refers to either the codomain or the image of the function, depending upon usage. This ambiguity is illustrated by the function f that maps real numbers to real numbers with f = x^2. Some books say that range of this function is its codomain, the set of all...
,
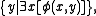 is a class. This gives us the existential quantifier. The universal quantifier can be defined in terms of the existential quantifier and negation
is a class. This gives us the existential quantifier. The universal quantifier can be defined in terms of the existential quantifier and negationNegation
In logic and mathematics, negation, also called logical complement, is an operation on propositions, truth values, or semantic values more generally. Intuitively, the negation of a proposition is true when that proposition is false, and vice versa. In classical logic negation is normally identified...
.
- Ranges: For any class R, the class
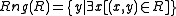 exists.
exists.
The above axioms can reorder the arguments of any relation so as to bring any desired argument to the front of the argument list, where it can be quantified.
Finally, each atomic formula
Atomic formula
In mathematical logic, an atomic formula is a formula with no deeper propositional structure, that is, a formula that contains no logical connectives or equivalently a formula that has no strict subformulas. Atoms are thus the simplest well-formed formulas of the logic...
implies the existence of a corresponding class relation:
- Membership: The class
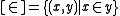 exists.
exists. - Diagonal: The class
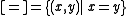 exists.
exists.
Diagonal, together with addition of dummy arguments and rearrangement of arguments, can build a relation asserting the equality of any two of its arguments; thus repeated variables can be handled.
Mendelson's variant
Mendelson (1997: 230) refers to his axioms B1-B7 of class comprehension as "axioms of class existence." Four of these identical to axioms already stated above: B1 is Membership; B2, Intersection; B3, Complement; B5, Product. B4 is Ranges modified to assert the existence of the domain of R (by existentially quantifying y instead of x). The last two axioms are:- B6:
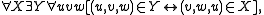
- B7:
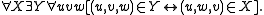
B6 and B7 enable what Converses and Association enable: given any class X of ordered triples, there exists another class Y whose members are the members of X each reordered in the same way.
Discussion
For a discussion of some ontologicalOntology
Ontology is the philosophical study of the nature of being, existence or reality as such, as well as the basic categories of being and their relations...
and other philosophical issues posed by NBG, especially when contrasted with ZFC and MK
Morse–Kelley set theory
In the foundation of mathematics, Morse–Kelley set theory or Kelley–Morse set theory is a first order axiomatic set theory that is closely related to von Neumann–Bernays–Gödel set theory...
, see Appendix C of Potter (2004).
Even though NBG is a conservative extension
Conservative extension
In mathematical logic, a logical theory T_2 is a conservative extension of a theory T_1 if the language of T_2 extends the language of T_1; every theorem of T_1 is a theorem of T_2; and any theorem of T_2 which is in the language of T_1 is already a theorem of T_1.More generally, if Γ is a set of...
of ZFC, a theorem may have a shorter and more elegant proof in NBG than in ZFC (or vice versa). For a survey of known results of this nature, see Pudlak (1998).
Model theory
ZFC, NBG, and MK have models describable in terms of V, the standard modelInner model
In mathematical logic, suppose T is a theory in the languageL = \langle \in \rangleof set theory.If M is a model of L describing a set theory and N is a class of M such that \langle N, \in_M, \ldots \rangle...
of ZFC and the von Neumann universe
Von Neumann universe
In set theory and related branches of mathematics, the von Neumann universe, or von Neumann hierarchy of sets, denoted V, is the class of hereditary well-founded sets...
. Now let the members of V include the inaccessible cardinal
Inaccessible cardinal
In set theory, an uncountable regular cardinal number is called weakly inaccessible if it is a weak limit cardinal, and strongly inaccessible, or just inaccessible, if it is a strong limit cardinal. Some authors do not require weakly and strongly inaccessible cardinals to be uncountable...
κ. Also let Def(X) denote the Δ0 definable subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
s of X (see constructible universe
Constructible universe
In mathematics, the constructible universe , denoted L, is a particular class of sets which can be described entirely in terms of simpler sets. It was introduced by Kurt Gödel in his 1938 paper "The Consistency of the Axiom of Choice and of the Generalized Continuum-Hypothesis"...
). Then:
- Vκ is an intended modelIntended interpretationOne who constructs a syntactical system usually has in mind from the outset some interpretation of this system. While this intended interpretation can have no explicit indication in the syntactical rules - since these rules must be strictly formal - the author's intention respecting...
of ZFC; - Def(Vκ) is an intended model of NBG;
- Vκ+1 is an intended model of MKMorse–Kelley set theoryIn the foundation of mathematics, Morse–Kelley set theory or Kelley–Morse set theory is a first order axiomatic set theory that is closely related to von Neumann–Bernays–Gödel set theory...
.
Category theory
The ontology of NBG provides scaffolding for speaking about "large objects" without risking paradox. In some developments of category theoryCategory theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, for instance, a "large category" is defined as one whose objects make up a proper class, with the same being true of its morphism
Morphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
s. A "small category", on the other hand, is one whose objects and morphisms are members of some set. We can thus easily speak of the "category of all sets" or "category of all small categories" without risking paradox. Those categories are large, of course. There is no "category of all categories" since it would have to contain the category of small categories, although yet another ontological extension can enable one to talk formally about such a "category" (see for example the "quasicategory of all categories" of Adámek et al. (1990), whose objects and morphisms form a "proper conglomerate").
On whether an ontology including classes as well as sets is adequate for category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, see Muller (2001).

