
Vector area
Encyclopedia
In geometry
, for a finite planar surface of scalar area
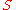 , the vector area
, the vector area
is defined as a vector whose magnitude is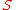 and whose direction is perpendicular to the plane, as determined by the right hand rule on the rim (moving one's right hand counterclockwise around the rim, when the palm of the hand is "touching" the surface, and the straight thumb indicates the direction).
and whose direction is perpendicular to the plane, as determined by the right hand rule on the rim (moving one's right hand counterclockwise around the rim, when the palm of the hand is "touching" the surface, and the straight thumb indicates the direction).

For an orientable surface S composed of a set of flat facet areas, the vector area of the surface is given by
of flat facet areas, the vector area of the surface is given by

where is the unit normal vector to the area
is the unit normal vector to the area 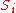 .
.
For bounded, oriented curved surfaces that are sufficiently well-behaved, we can still define vector area. First, we split the surface into infinitesimal elements, each of which is effectively flat. For each infinitesimal element of area, we have an area vector, also infinitesimal.

where is the local unit vector perpendicular to
is the local unit vector perpendicular to 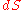 . Integrating gives the vector area for the surface.
. Integrating gives the vector area for the surface.
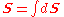
For a curved or faceted surface, the vector area is smaller in magnitude than the area. As an extreme example, a closed surface can possess arbitrarily large area, but its vector area is necessarily zero. Surfaces that share a boundary may have very different areas, but they must have the same vector area---the vector area is entirely determined by the boundary. These are consequences of Stokes theorem.
The concept of an area vector simplifies the equation for determining the flux
through the surface. Consider a planar surface in a uniform field
. The flux can be written as the dot product
of the field and area vector. This is much simpler than multiplying the field strength by the surface area and the cosine of the angle between the field and the surface normal.

where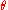 is the angle between the plane normal and the z-axis.
is the angle between the plane normal and the z-axis.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, for a finite planar surface of scalar area
Area
Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
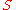 , the vector area
, the vector area
is defined as a vector whose magnitude is
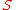 and whose direction is perpendicular to the plane, as determined by the right hand rule on the rim (moving one's right hand counterclockwise around the rim, when the palm of the hand is "touching" the surface, and the straight thumb indicates the direction).
and whose direction is perpendicular to the plane, as determined by the right hand rule on the rim (moving one's right hand counterclockwise around the rim, when the palm of the hand is "touching" the surface, and the straight thumb indicates the direction).
For an orientable surface S composed of a set
 of flat facet areas, the vector area of the surface is given by
of flat facet areas, the vector area of the surface is given by
where
 is the unit normal vector to the area
is the unit normal vector to the area 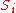 .
.For bounded, oriented curved surfaces that are sufficiently well-behaved, we can still define vector area. First, we split the surface into infinitesimal elements, each of which is effectively flat. For each infinitesimal element of area, we have an area vector, also infinitesimal.

where
 is the local unit vector perpendicular to
is the local unit vector perpendicular to 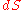 . Integrating gives the vector area for the surface.
. Integrating gives the vector area for the surface.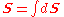
For a curved or faceted surface, the vector area is smaller in magnitude than the area. As an extreme example, a closed surface can possess arbitrarily large area, but its vector area is necessarily zero. Surfaces that share a boundary may have very different areas, but they must have the same vector area---the vector area is entirely determined by the boundary. These are consequences of Stokes theorem.
The concept of an area vector simplifies the equation for determining the flux
Flux
In the various subfields of physics, there exist two common usages of the term flux, both with rigorous mathematical frameworks.* In the study of transport phenomena , flux is defined as flow per unit area, where flow is the movement of some quantity per time...
through the surface. Consider a planar surface in a uniform field
Field (physics)
In physics, a field is a physical quantity associated with each point of spacetime. A field can be classified as a scalar field, a vector field, a spinor field, or a tensor field according to whether the value of the field at each point is a scalar, a vector, a spinor or, more generally, a tensor,...
. The flux can be written as the dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
of the field and area vector. This is much simpler than multiplying the field strength by the surface area and the cosine of the angle between the field and the surface normal.
Projection of area onto planes
The projected area onto (for example) the x-y plane is equivalent to the z-component of the vector area, and is given by
where
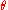 is the angle between the plane normal and the z-axis.
is the angle between the plane normal and the z-axis.

