Vector-valued form
Encyclopedia
In mathematics
, a vector-valued differential form on a manifold
M is a differential form
on M with values in a vector space
V. More generally, it is a differential form with values in some vector bundle
E over M. Ordinary differential forms can be viewed as R-valued differential forms. Vector-valued forms are natural objects in differential geometry and have numerous applications.
over M. We denote the space of smooth section
s of a bundle E by Γ(E). A E-valued differential form of degree p is a smooth section of the tensor product
bundle of E with Λp(T*M), the p-th exterior power of the cotangent bundle
of M. The space of such forms is denoted by
Because Γ is a monoidal functor
, this can also be interpreted as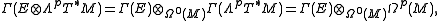
where the latter two tensor products are the tensor product of modules
over the ring
Ω0(M) of smooth R-valued functions on M (see the fifth example here). By convention, an E-valued 0-form is just a section of the bundle E. That is,
Equivalently, a E-valued differential form can be defined as a bundle morphism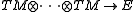
which is totally skew-symmetric.
Let V be a fixed vector space
. A V-valued differential form of degree p is a differential form of degree p with values in the trivial bundle M × V. The space of such forms is denoted Ωp(M, V). When V = R one recovers the definition of an ordinary differential form. If V is finite-dimensional, then one can show that the natural homomorphism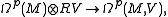
where the first tensor product is of vector spaces over R, is an isomorphism. One can verify this for p=0 by turning a basis for V into a set of constant functions to V, which allows the construction of an inverse to the above homomorphism. The general case can be proved by noting that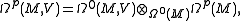
and that because R is a sub-ring of Ω0(M) via the constant functions,
of E by φ.
The formula is given just as in the ordinary case. For any E-valued p-form ω on N the pullback φ*ω is given by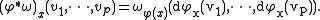
The definition is just as for ordinary forms with the exception that real multiplication is replaced with the tensor product
:
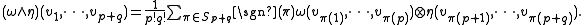
In particular, the wedge product of an ordinary (R-valued) p-form with an E-valued q-form is naturally an E-valued (p+q)-form (since the tensor product of E with the trivial bundle M × R is naturally isomorphic to E). For ω ∈ Ωp(M) and η ∈ Ωq(M, E) one has the usual commutativity relation:
In general, the wedge product of two E-valued forms is not another E-valued form, but rather an (EE)-valued form. However, if E is an algebra bundle
(i.e. a bundle of algebra
s rather than just vector spaces) one can compose with multiplication in E to obtain an E-valued form. If E is a bundle of commutative
, associative algebra
s then, with this modified wedge product, the set of all E-valued differential forms
becomes a graded-commutative associative algebra. If the fibers of E are not commutative then Ω(M,E) will not be graded-commutative.
on the space of V-valued forms. This is just the ordinary exterior derivative acting component-wise relative to any basis
of V. Explicitly, if {eα} is a basis for V then the differential of a V-valued p-form ω = ωαeα is given by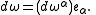
The exterior derivative on V-valued forms is completely characterized by the usual relations:
More generally, the above remarks apply to E-valued forms where E is any flat vector bundle
over M (i.e. a vector bundle whose transition functions are constant). The exterior derivative is defined as above on any local trivialization of E.
If E is not flat then there is no natural notion of an exterior derivative acting on E-valued forms. What is needed is a choice of connection
on E. A connection on E is a linear differential operator
taking sections of E to E-valued one forms: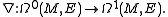
If E is equipped with a connection ∇ then there is a unique covariant exterior derivative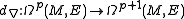
extending ∇. The covariant exterior derivative is characterized by linearity and the equation
where ω is a E-valued p-form and η is an ordinary q-form. In general, one need not have d∇2 = 0. In fact, this happens if and only if the connection ∇ is flat (i.e. has vanishing curvature).
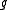-valued forms where 
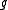is a Lie algebra
. Such forms have important applications in the theory of connections
on a principal bundle
as well as in the theory of Cartan connection
s.
Since every Lie algebra has a bilinear Lie bracket
operation, the wedge product of two Lie algebra-valued forms can be composed with the bracket operation to obtain another Lie algebra-valued form. This operation is usually denoted [ω∧η] to indicate both operations involved. For example, if ω and η are Lie algebra-valued one forms, then one has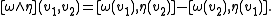
With this operation the set of all Lie algebra-valued forms on a manifold M becomes a graded Lie superalgebra.
) frame bundle
of E, which is a principal
GLk(R) bundle over M. The pullback
of E by π is isomorphic to the trivial bundle F(E) × Rk. Therefore, the pullback by π of an E-valued form on M determines an Rk-valued form on F(E). It is not hard to check that this pulled back form is right-equivariant
with respect to the natural action
of GLk(R) on F(E) × Rk and vanishes on vertical vectors
(tangent vectors to F(E) which lie in the kernel of dπ). Such vector-valued forms on F(E) are important enough to warrant special terminology: they are called basic or tensorial forms on F(E).
Let π : P → M be a (smooth) principal G-bundle
and let V be a fixed vector space together with a representation
ρ : G → GL(V). A basic or tensorial form on P of type ρ is a V-valued form ω on P which is equivariant and horizontal in the sense that
Here Rg denotes right-translation by g ∈ G. Note that for 0-forms the second condition is vacuously true.
Given P and ρ as above one can construct the associated vector bundle E = P ×ρ V. Tensorial forms on P are in one-to-one correspondence with E-valued forms on M. As in the case of the principal bundle F(E) above, E-valued forms on M pull back to V-valued forms on P. These are precisely the basic or tensorial forms on P of type ρ. Conversely given any tensorial form on P of type ρ one can construct the associated E-valued form on M in a straightforward manner.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a vector-valued differential form on a manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
M is a differential form
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
on M with values in a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
V. More generally, it is a differential form with values in some vector bundle
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
E over M. Ordinary differential forms can be viewed as R-valued differential forms. Vector-valued forms are natural objects in differential geometry and have numerous applications.
Formal definition
Let M be a smooth manifold and E → M be a smooth vector bundleVector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
over M. We denote the space of smooth section
Section (fiber bundle)
In the mathematical field of topology, a section of a fiber bundle π is a continuous right inverse of the function π...
s of a bundle E by Γ(E). A E-valued differential form of degree p is a smooth section of the tensor product
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
bundle of E with Λp(T*M), the p-th exterior power of the cotangent bundle
Cotangent bundle
In mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold...
of M. The space of such forms is denoted by
Because Γ is a monoidal functor
Monoidal functor
In category theory, monoidal functors are functors between monoidal categories which preserve the monoidal structure. More specifically, a monoidal functor between two monoidal categories consists of a functor between the categories, along with two coherence maps—a natural transformation and a...
, this can also be interpreted as
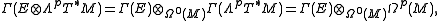
where the latter two tensor products are the tensor product of modules
Tensor product of modules
In mathematics, the tensor product of modules is a construction that allows arguments about bilinear maps to be carried out in terms of linear maps...
over the ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
Ω0(M) of smooth R-valued functions on M (see the fifth example here). By convention, an E-valued 0-form is just a section of the bundle E. That is,
Equivalently, a E-valued differential form can be defined as a bundle morphism
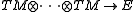
which is totally skew-symmetric.
Let V be a fixed vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
. A V-valued differential form of degree p is a differential form of degree p with values in the trivial bundle M × V. The space of such forms is denoted Ωp(M, V). When V = R one recovers the definition of an ordinary differential form. If V is finite-dimensional, then one can show that the natural homomorphism
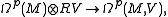
where the first tensor product is of vector spaces over R, is an isomorphism. One can verify this for p=0 by turning a basis for V into a set of constant functions to V, which allows the construction of an inverse to the above homomorphism. The general case can be proved by noting that
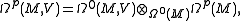
and that because R is a sub-ring of Ω0(M) via the constant functions,
Pullback
One can define the pullback of vector-valued forms by smooth maps just as for ordinary forms. The pullback of an E-valued form on N by a smooth map φ : M → N is an (φ*E)-valued form on M, where φ*E is the pullback bundlePullback bundle
In mathematics, a pullback bundle or induced bundle is a useful construction in the theory of fiber bundles. Given a fiber bundle π : E → B and a continuous map f : B′ → B one can define a "pullback" of E by f as a bundle f*E over B′...
of E by φ.
The formula is given just as in the ordinary case. For any E-valued p-form ω on N the pullback φ*ω is given by
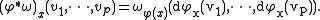
Wedge product
Just as for ordinary differential forms, one can define a wedge product of vector-valued forms. The wedge product of a E1-valued p-form with a E2-valued q-form is naturally a (E1E2)-valued (p+q)-form:The definition is just as for ordinary forms with the exception that real multiplication is replaced with the tensor product
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
:
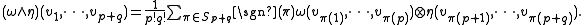
In particular, the wedge product of an ordinary (R-valued) p-form with an E-valued q-form is naturally an E-valued (p+q)-form (since the tensor product of E with the trivial bundle M × R is naturally isomorphic to E). For ω ∈ Ωp(M) and η ∈ Ωq(M, E) one has the usual commutativity relation:
In general, the wedge product of two E-valued forms is not another E-valued form, but rather an (EE)-valued form. However, if E is an algebra bundle
Algebra bundle
In mathematics, an algebra bundle is a fiber bundle whose fibers are algebras and local trivializations respect the algebra structure. It follows that the transition functions are algebra isomorphisms...
(i.e. a bundle of algebra
Algebra over a field
In mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
s rather than just vector spaces) one can compose with multiplication in E to obtain an E-valued form. If E is a bundle of commutative
Commutative algebra
Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
, associative algebra
Associative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
s then, with this modified wedge product, the set of all E-valued differential forms
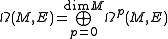
becomes a graded-commutative associative algebra. If the fibers of E are not commutative then Ω(M,E) will not be graded-commutative.
Exterior derivative
For any vector space V there is a natural exterior derivativeExterior derivative
In differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
on the space of V-valued forms. This is just the ordinary exterior derivative acting component-wise relative to any basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
of V. Explicitly, if {eα} is a basis for V then the differential of a V-valued p-form ω = ωαeα is given by
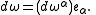
The exterior derivative on V-valued forms is completely characterized by the usual relations:
More generally, the above remarks apply to E-valued forms where E is any flat vector bundle
Flat vector bundle
In mathematics, a vector bundle is said to be flat if it is endowed with a affine connection with vanishing curvature, ie. a flat connection.-de Rham cohomology of a flat vector bundle:...
over M (i.e. a vector bundle whose transition functions are constant). The exterior derivative is defined as above on any local trivialization of E.
If E is not flat then there is no natural notion of an exterior derivative acting on E-valued forms. What is needed is a choice of connection
Connection (vector bundle)
In mathematics, a connection on a fiber bundle is a device that defines a notion of parallel transport on the bundle; that is, a way to "connect" or identify fibers over nearby points. If the fiber bundle is a vector bundle, then the notion of parallel transport is required to be linear...
on E. A connection on E is a linear differential operator
Differential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
taking sections of E to E-valued one forms:
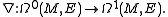
If E is equipped with a connection ∇ then there is a unique covariant exterior derivative
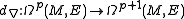
extending ∇. The covariant exterior derivative is characterized by linearity and the equation
where ω is a E-valued p-form and η is an ordinary q-form. In general, one need not have d∇2 = 0. In fact, this happens if and only if the connection ∇ is flat (i.e. has vanishing curvature).
Lie algebra-valued forms
An important case of vector-valued differential forms are Lie algebra-valued forms. These are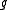-valued forms where 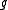is a Lie algebraLie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
. Such forms have important applications in the theory of connections
Connection (principal bundle)
In mathematics, a connection is a device that defines a notion of parallel transport on the bundle; that is, a way to "connect" or identify fibers over nearby points...
on a principal bundle
Principal bundle
In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
as well as in the theory of Cartan connection
Cartan connection
In the mathematical field of differential geometry, a Cartan connection is a flexible generalization of the notion of an affine connection. It may also be regarded as a specialization of the general concept of a principal connection, in which the geometry of the principal bundle is tied to the...
s.
Since every Lie algebra has a bilinear Lie bracket
Lie bracket
Lie bracket can refer to:*A bilinear binary operation defined on elements of a Lie algebra*Lie bracket of vector fields...
operation, the wedge product of two Lie algebra-valued forms can be composed with the bracket operation to obtain another Lie algebra-valued form. This operation is usually denoted [ω∧η] to indicate both operations involved. For example, if ω and η are Lie algebra-valued one forms, then one has
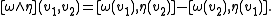
With this operation the set of all Lie algebra-valued forms on a manifold M becomes a graded Lie superalgebra.
Basic or tensorial forms on principal bundles
Let E → M be a smooth vector bundle of rank k over M and let π : F(E) → M be the (associatedAssociated bundle
In mathematics, the theory of fiber bundles with a structure group G allows an operation of creating an associated bundle, in which the typical fiber of a bundle changes from F_1 to F_2, which are both topological spaces with a group action of G...
) frame bundle
Frame bundle
In mathematics, a frame bundle is a principal fiber bundle F associated to any vector bundle E. The fiber of F over a point x is the set of all ordered bases, or frames, for Ex...
of E, which is a principal
Principal bundle
In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
GLk(R) bundle over M. The pullback
Pullback bundle
In mathematics, a pullback bundle or induced bundle is a useful construction in the theory of fiber bundles. Given a fiber bundle π : E → B and a continuous map f : B′ → B one can define a "pullback" of E by f as a bundle f*E over B′...
of E by π is isomorphic to the trivial bundle F(E) × Rk. Therefore, the pullback by π of an E-valued form on M determines an Rk-valued form on F(E). It is not hard to check that this pulled back form is right-equivariant
Equivariant
In mathematics, an equivariant map is a function between two sets that commutes with the action of a group. Specifically, let G be a group and let X and Y be two associated G-sets. A function f : X → Y is said to be equivariant iffor all g ∈ G and all x in X...
with respect to the natural action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
of GLk(R) on F(E) × Rk and vanishes on vertical vectors
Vertical bundle
The vertical bundle of a smooth fiber bundle is the subbundle of the tangent bundle that consists of all vectors which are tangent to the fibers...
(tangent vectors to F(E) which lie in the kernel of dπ). Such vector-valued forms on F(E) are important enough to warrant special terminology: they are called basic or tensorial forms on F(E).
Let π : P → M be a (smooth) principal G-bundle
Principal bundle
In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
and let V be a fixed vector space together with a representation
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
ρ : G → GL(V). A basic or tensorial form on P of type ρ is a V-valued form ω on P which is equivariant and horizontal in the sense that
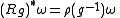for all g ∈ G, and
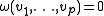whenever at least one of the vi are vertical (i.e., dπ(vi) = 0).
Here Rg denotes right-translation by g ∈ G. Note that for 0-forms the second condition is vacuously true.
Given P and ρ as above one can construct the associated vector bundle E = P ×ρ V. Tensorial forms on P are in one-to-one correspondence with E-valued forms on M. As in the case of the principal bundle F(E) above, E-valued forms on M pull back to V-valued forms on P. These are precisely the basic or tensorial forms on P of type ρ. Conversely given any tensorial form on P of type ρ one can construct the associated E-valued form on M in a straightforward manner.