Vacuum solution (general relativity)
Encyclopedia
In general relativity
, a vacuum solution is a Lorentzian manifold whose Einstein tensor
vanishes identically. According to the Einstein field equation, this means that the stress-energy tensor
also vanishes identically, so that no matter or non-gravitational fields are present.
More generally, a vacuum region in a Lorentzian manifold is a region in which the Einstein tensor vanishes.
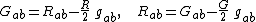
where the trace
s are
.
A third equivalent condition follows from the Ricci decomposition
of the Riemann curvature tensor
as a sum of the Weyl curvature tensor plus terms built out of the Ricci tensor: the Weyl and Riemann tensors agree,
, in some region if and only if it is a vacuum region.
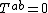in a vacuum region, it might seem that according to general relativity, vacuum regions must contain no energy
. But the gravitational field can do work, so we must expect the gravitational field itself to possess energy, and it does. However, determining the precise location of this gravitational field energy is technically problematical in general relativity, by its very nature of the clean separation into a universal gravitational interaction and "all the rest".
The fact that the gravitational field itself possesses energy yields a way to understand the nonlinearity of the Einstein field equation: this gravitational field energy itself produces more gravity. This means that the gravitational field outside the Sun is a bit stronger according to general relativity than it is according to Newton's theory.
These all belong to one or more general families of solutions:
Several of the families mentioned here, members of which are obtained by solving an appropriate linear or nonlinear, real or complex partial differential equation, turn out to be very closely related, in perhaps surprising ways.
In addition to these, we also have the vacuum pp-wave spacetimes, which include the gravitational plane wave
s.
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, a vacuum solution is a Lorentzian manifold whose Einstein tensor
Einstein tensor
In differential geometry, the Einstein tensor , named after Albert Einstein, is used to express the curvature of a Riemannian manifold...
vanishes identically. According to the Einstein field equation, this means that the stress-energy tensor
Stress-energy tensor
The stress–energy tensor is a tensor quantity in physics that describes the density and flux of energy and momentum in spacetime, generalizing the stress tensor of Newtonian physics. It is an attribute of matter, radiation, and non-gravitational force fields...
also vanishes identically, so that no matter or non-gravitational fields are present.
More generally, a vacuum region in a Lorentzian manifold is a region in which the Einstein tensor vanishes.
Equivalent conditions
It is a mathematical fact that the Einstein tensor vanishes if and only if the Ricci tensor vanishes. This follows from the fact that these two second rank tensors stand in a kind of dual relationship; they are the trace reverse of each other: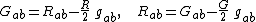where the trace
Trace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
s are
.A third equivalent condition follows from the Ricci decomposition
Ricci decomposition
In semi-Riemannian geometry, the Ricci decomposition is a way of breaking up the Riemann curvature tensor of a pseudo-Riemannian manifold into pieces with useful individual algebraic properties...
of the Riemann curvature tensor
Riemann curvature tensor
In the mathematical field of differential geometry, the Riemann curvature tensor, or Riemann–Christoffel tensor after Bernhard Riemann and Elwin Bruno Christoffel, is the most standard way to express curvature of Riemannian manifolds...
as a sum of the Weyl curvature tensor plus terms built out of the Ricci tensor: the Weyl and Riemann tensors agree,
, in some region if and only if it is a vacuum region.Gravitational energy
Since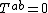 in a vacuum region, it might seem that according to general relativity, vacuum regions must contain no energyEnergy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
. But the gravitational field can do work, so we must expect the gravitational field itself to possess energy, and it does. However, determining the precise location of this gravitational field energy is technically problematical in general relativity, by its very nature of the clean separation into a universal gravitational interaction and "all the rest".
The fact that the gravitational field itself possesses energy yields a way to understand the nonlinearity of the Einstein field equation: this gravitational field energy itself produces more gravity. This means that the gravitational field outside the Sun is a bit stronger according to general relativity than it is according to Newton's theory.
Examples
Well known examples of explicit vacuum solutions include:- Minkowski spacetime (which describes empty space with no cosmological constantCosmological constantIn physical cosmology, the cosmological constant was proposed by Albert Einstein as a modification of his original theory of general relativity to achieve a stationary universe...
) - Milne modelMilne modelThe Milne model was a special relativistic cosmological model proposed by Edward Arthur Milne in 1935. It is mathematically equivalent to a special case of the FLRW model in the limit of zero energy density , and it obeys the cosmological principle...
(which is a model developed by E. A. Milne describing an empty universe which has no curvature) - Schwarzschild vacuum (which describes the spacetime geometry around a spherical mass),
- Kerr vacuum (which describes the geometry around a rotating object),
- Taub-NUT vacuumTaub-NUT vacuumThe Taub-NUT vacuum is an exact solution to Einstein's equations, a model universe formulated in the framework of general relativity that is homogeneous but anisotropic. It is based on a solution published by Abraham Haskel Taub in 1951....
(a famous counterexample describing the exterior gravitational field of an isolated object with strange properties), - Kerns–Wild vacuum (Robert M. Kerns and Walter J. Wild 1982) (a Schwarzschild object immersed in an ambient "almost uniform" gravitational field),
- double Kerr vacuum (two Kerr objects sharing the same axis of rotation, but held apart by unphysical zero active mass "cables" going out to suspension points infinitely removed),
- Khan–Penrose vacuum (K. A. Khan and Roger PenroseRoger PenroseSir Roger Penrose OM FRS is an English mathematical physicist and Emeritus Rouse Ball Professor of Mathematics at the Mathematical Institute, University of Oxford and Emeritus Fellow of Wadham College...
1971) (a simple colliding plane wave model), - Oszváth–Schücking vacuum (the circularly polarized sinusoidal gravitational wave, another famous counterexample).
- Kasner metricKasner metricThe Kasner metric is an exact solution to Einstein's theory of general relativity. It describes an anisotropic universe without matter...
These all belong to one or more general families of solutions:
- the Weyl vacua (Hermann WeylHermann WeylHermann Klaus Hugo Weyl was a German mathematician and theoretical physicist. Although much of his working life was spent in Zürich, Switzerland and then Princeton, he is associated with the University of Göttingen tradition of mathematics, represented by David Hilbert and Hermann Minkowski.His...
) (the family of all static vacuum solutions), - the Beck vacua (Guido Beck 1925) (the family of all cylindrically symmetric nonrotating vacuum solutions),
- the Ernst vacua (Frederick J. Ernst 1968) (the family of all stationary axisymmetric vacuum solutions),
- the Ehlers vacua (Jürgen EhlersJürgen EhlersJürgen Ehlers was a German physicist who made notable contributions to the current understanding of Albert Einstein's theory of general relativity...
) (the family of all cylindrically symmetric vacuum solutions), - the Szekeres vacua (George SzekeresGeorge SzekeresGeorge Szekeres AM was a Hungarian-Australian mathematician.-Early years:Szekeres was born in Budapest, Hungary as Szekeres György and received his degree in chemistry at the Technical University of Budapest. He worked six years in Budapest as an analytical chemist. He married Esther Klein in 1936...
) (the family of all colliding gravitational plane wave models), - the Gowdy vacua (Robert H. Gowdy) (cosmological models constructed using gravitational waves),
Several of the families mentioned here, members of which are obtained by solving an appropriate linear or nonlinear, real or complex partial differential equation, turn out to be very closely related, in perhaps surprising ways.
In addition to these, we also have the vacuum pp-wave spacetimes, which include the gravitational plane wave
Gravitational plane wave
In general relativity, a gravitational plane wave is a special class of a vacuum pp-wave spacetime, and may be defined in terms of Brinkmann coordinates byds^2=[a+2bxy]du^2+2dudv+dx^2+dy^2...
s.
See also
- vacuum solutionVacuum solutionA vacuum solution is a solution of a field equation in which the sources of the field are taken to be identically zero. That is, such field equations are written without matter interaction .-Examples:...
, an article about vacuum solutions in physics in general, - lambdavacuum solutionLambdavacuum solutionIn general relativity, a lambdavacuum solution is an exact solution to the Einstein field equation in which the only term in the stress-energy tensor is a cosmological constant term...
, an article about a significant generalization of the notion of a vacuum solution in general relativity, - exact solutions in general relativityExact solutions in general relativityIn general relativity, an exact solution is a Lorentzian manifold equipped with certain tensor fields which are taken to model states of ordinary matter, such as a fluid, or classical nongravitational fields such as the electromagnetic field....
, an article about all kinds of exact solutions to the Einstein field equation.